High frequency questions (I)
1, Reverse linked list (206)
Title Description:

Note: the more accurate expression should be that the result of inversion is 1 ⬅ two ⬅ three ⬅ four ⬅ 5. In other words, the node value cannot be simply changed
1. Double pointer iteration
Idea:
Create two pointers pre and cur. Pre initially points to null and cur initially points to head (pre is always the previous node of cur). The two pointers continuously traverse the linked list backward. Cur points to pre in each iteration, and then pre and cur move backward one bit at the same time.
be careful:
Before pointing cur to pre, you need to set cur Next is saved in the temp variable to ensure access to the next node of cur (used to move backward). The diagram is as follows:
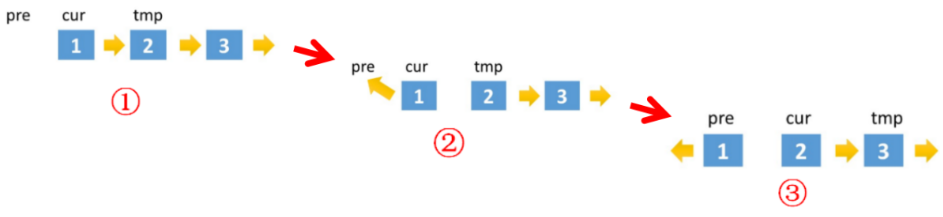
Code implementation:
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode reverseList(ListNode head) {
ListNode pre = null;
ListNode cur = head;
ListNode temp = null;
while(cur!=null) {
//Record the next node of the current node
temp = cur.next;
//Point the current node to pre
cur.next = pre;
//Both pre and cur nodes are moved back one bit
pre = cur;
cur = temp;
}
return pre;
}
}
Time complexity O(n)
Space complexity O(1)
2. Recursion
Idea:
Recurs from the first node to the last node, and record the last node with cur (the final result is returned from cur). When traversing to the last node, the recursion ends and backtracking begins, and the penultimate node next.next = penultimate node (change the pointing of the last node of the penultimate node to the penultimate node), continue to point backward until the first node, and return cur. The diagram is as follows:
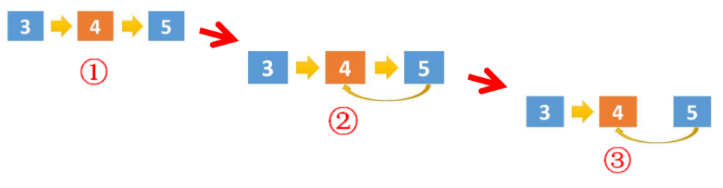
Code implementation:
class Solution {
public ListNode reverseList(ListNode head) {
//The first condition prevents the linked list from being empty, and the second condition recurses to the last node
if(head==null || head.next==null) {
return head;
}
//Cur is the last node, and the value of cur will not change
//When head is the penultimate node, the last recursive return is the last node
ListNode cur = reverseList(head.next);
//4.next.next = 4; Represents 5 to 4
head.next.next = head;
//Prevent 5 and 4 from forming a cycle, and it is not necessary to point 4 to 5
head.next = null;
//Each layer of recursion returns the constant cur value, that is, the last node
return cur;
}
}
Time complexity O(n)
Space complexity O(n), recursive use of stack space
2, Longest string without duplicate characters (3)
Title Description:
Given a string, please find the length of the longest substring that does not contain duplicate characters.

Idea: sliding window

By observing the above process, it can be found that if the left character in the string is selected as the starting position, and it is obtained that the end position of the longest substring without repeated characters is right, that is, the right + 1 position is repeated, then it is necessary to re select the left + 1 character as the starting position. At this time, the characters from left + 1 to right are obviously not repeated, Since the original left character is missing (the left character will also be deleted from the non repeating substring), you can continue to expand right until a repeating character appears on the right.
The left and right boundaries only expand to the right, not shrink or reset.
Code implementation:
Note: note the two method names of HashSet: contains and add
class Solution {
public int lengthOfLongestSubstring(String s) {
HashSet<Character> hashSet = new HashSet<>();
int right = 0;
int maxLen = 0; //Record the length of the longest non repeating substring
//Each time the for loop is executed, it means that the left judgment is completed and the left+1 position needs to be judged
for (int left = 0; left < s.length(); left++) {
//Each round needs to remove the left of the previous round from the substring
if (left != 0) {
hashSet.remove(s.charAt(left - 1));
}
//Move right to the right until a duplicate character appears
while (right < s.length() && !hashSet.contains(s.charAt(right))) {
hashSet.add(s.charAt(right));
right++;
}
//The right value does not reset, it only increases
maxLen = Math.max(maxLen, right - left);
//Due to the execution of right + +, right will eventually come to the position of the first repeated character
}
return maxLen;
}
}

3, LRU caching mechanism (146)
1. Title Description
Using the data structure you have mastered, design and implement an LRU (least recently used) caching mechanism
Implement LRUmap class:
- LRUmap(int capacity) initializes LRU cache with positive integer as capacity
- int get(int key) if the keyword key exists in the cache, the value of the keyword is returned; otherwise, - 1 is returned
- void put(int key, int value) if the keyword already exists, change its data value; If the keyword does not exist, insert the group keyword value. When the cache capacity reaches the maximum capacity, the longest unused data value should be deleted before writing new data, so as to make room for new data values
2. Introduction of LRU algorithm
-
The full name is least recently used. It is a cache elimination strategy, that is, it is considered that the recently used data should be useful, and the data that has not been used for a long time should be useless. When the memory is full, priority will be given to deleting the data that has not been used for a long time
-
Corresponding to the data structure description, the most frequently used elements are moved to the head or tail, which will lead to the passive movement of elements that have not been used for a long time to the other side. The first deleted element is the element that has not been used for the longest time (note that it is not the element that has been used the least, this is the LFU algorithm)
- When you get an element, you access the element. You need to move the element to the head or tail, indicating that it has been used recently
- When you put an element, you access the element. You need to insert this element into the head or tail, indicating that it has been used recently
3. Selection of data structure
3.1 why not use arrays?
The time complexity of finding an element in the array is O(1), but the time complexity of moving the element as a whole after deleting the element is O(n), which does not meet the meaning of the question
3.2 why not use one-way linked list?
The time complexity of adding / deleting elements in the linked list is O(1). If the head node is deleted, it meets the meaning of the question
However, if the intermediate node of the linked list is deleted, the previous node of the node to be deleted needs to be saved, and the time complexity of traversing to the node to be deleted is O(n), which does not meet the meaning of the problem
3.3 why use HashMap + bidirectional linked list?
HashMap only needs O(1) time complexity to find the node to be deleted
To delete a node in a two-way linked list, you do not need to traverse to find the previous node of the node to be deleted, so the time complexity of deleting an element at any position is O(1)
To sum up: using HashMap to find nodes and bidirectional linked list to delete / move nodes can meet the requirements of time complexity of O(1)
The overall structure is shown in the figure below:

4. Code implementation
Move the element that has just been used to the head and the element that has not been used for a long time to the tail
public class LRUCache {
//Node of bidirectional linked list
class DLinkedNode { //Note that the class initial of the inner class is lowercase
int key; //The key is consistent with the key content of the Map
int value;
DLinkedNode prev;
DLinkedNode next;
public DLinkedNode() {}
public DLinkedNode(int _key, int _value) {key = _key; value = _value;}
}
private Map<Integer, DLinkedNode> map = new HashMap<Integer, DLinkedNode>();
private int size; //Actual number of elements
private int capacity; //capacity
private DLinkedNode head, tail;
//constructor
public LRUCache(int capacity) {
this.size = 0;
this.capacity = capacity;
//Use pseudo header and pseudo tail nodes
head = new DLinkedNode(); //The pseudo header node is the previous node of the first node
tail = new DLinkedNode(); //The pseudo tail node is the last node after the last node
//The pseudo head and tail nodes should be connected together during initialization
head.next = tail;
tail.prev = head;
}
//get method
public int get(int key) {
DLinkedNode node = map.get(key);
if (node == null) {
return -1;
}
//If the key exists, first locate it through the HashMap, and then move it to the head
moveToHead(node);
return node.value;
}
//put method
public void put(int key, int value) {
DLinkedNode node = map.get(key);
if (node == null) {
//If the key does not exist, create a new node
DLinkedNode newNode = new DLinkedNode(key, value);
//Add to hash table
map.put(key, newNode);
//Add to the header of a two-way linked list
addToHead(newNode);
++size;
if (size > capacity) {
//If the number of elements exceeds the capacity, delete the tail node of the two-way linked list
DLinkedNode tail = removeTail();
//Delete the corresponding entry in the hash table
map.remove(tail.key);
--size;
}
}
else {
//If the key exists, first locate it through the HashMap, then modify the value and move it to the header
node.value = value;
moveToHead(node);
}
}
//Move node to head
private void moveToHead(DLinkedNode node) {
removeNode(node); //Disconnect this node from the linked list
addToHead(node); //Move the disconnected node to the head
}
//Disconnect the node from the linked list
private void removeNode(DLinkedNode node) {
node.prev.next = node.next;
node.next.prev = node.prev;
}
//Move node to head (modify four pointers)
//First modify the two pointers of the inserted node
private void addToHead(DLinkedNode node) {
node.prev = head; //The pseudo header node becomes the previous node of this node
node.next = head.next; //The original first node becomes the next node of this node
head.next.prev = node; //The forward pointer of the original first node points to this node
head.next = node; //This node becomes the last node of the pseudo header node
}
//Delete the tail node of the linked list
//The tail node is used here only
private DLinkedNode removeTail() {
DLinkedNode res = tail.prev; //What is deleted is actually the previous node of the pseudo tail
removeNode(res);
return res;
}
}
4, The k th largest element in the array (215)
Title Description:
The kth largest element was found in an unordered array. Note that you need to find the value of the kth largest element of the array, not the kth element
1. Fast exhaust deformation
Idea:
Using the fast scheduling method, judge the position of the benchmark number after exchange. If the index of the benchmark number is m after division and exchange, judge whether M is equal to arr.length - k. if it is equal to, directly return the element at M position. If it is less than, recurs the right sub interval, otherwise recurs the left sub interval
Code implementation:
class Solution {
public int findKthLargest(int[] arr, int k) {
//Recursively divide the array (less than / greater than the area and then divide), and finally determine the minimum number of k
return partitionArray(arr, 0, arr.length - 1, arr.length - k);
}
int partitionArray(int[] arr, int lo, int hi, int k) {
//Random fast scheduling can be used
//Call the partition method to partition once, and the return value is the index position of the benchmark number
int m = partition(arr, lo, hi);
//If equal to, the element at position m is returned directly. If less than, the right sub interval is recursive, otherwise the left sub interval is recursive
if (m == k) {
return arr[m];
} else {
return m < k ? partitionArray(arr, m + 1, hi, k) : partitionArray(arr, lo, m - 1, k);
}
}
//The return value is the index position of the reference number
int partition(int[] arr, int l, int r) {
int less = l - 1;
int more = r;
while (l < more) {
if (arr[l] < arr[r]) {
swap(arr, ++less, l++);
} else if (arr[l] > arr[r]) {
swap(arr, --more, l);
} else {
l++;
}
}
swap(arr, r, more);
return more;
}
void swap(int[] a, int i, int j) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
-
Time complexity: O(n) (after using random fast scheduling)
-
Space complexity: O(logn). The space cost of recursive use of stack space is expected to be O(logn)
2. Large top pile
**Idea: * * using the idea of heap sorting, construct a large top heap, exchange the top element and the last element k - 1 times (and reduce the heap length by one), and then return to the top element.
Code implementation:
class Solution {
public int findKthLargest(int[] nums, int k) {
for (int i = 0; i < nums.length; i++) {
heapInsert(nums, i);
}
int size = nums.length;
//Cannot exchange here
//The cycle condition is k-1 times
for (int i = 0; i < k - 1; i++) {
//During the exchange, the size should be transferred in during the adjustment
swap(nums, 0, --size);
heapify(nums, 0, size);
}
return nums[0];
}
public void heapInsert(int[] arr, int i) {
while (arr[i] > arr[(i - 1) / 2]) {
swap(arr, i, (i - 1) / 2);
i = (i - 1) / 2;
}
}
public void heapify(int[] arr, int i, int size) {
int left = i * 2 + 1;
while (left < size) {
int largest = left + 1 < size && arr[left + 1] > arr[left] ? left + 1 : left;
largest = arr[largest] > arr[i] ? largest : i;
if (arr[largest] == arr[i]) {
break;
}
swap(arr, i, largest);
i = largest;
left = i * 2 + 1;
}
}
public void swap(int[] arr, int l, int r) {
int temp = arr[l];
arr[l] = arr[r];
arr[r] = temp;
}
}
- Time complexity: O(nlogn), the time cost of heap building is O(n), and the total cost of deletion is O(klogn). Because K < n, the progressive time complexity is O(n+klogn)=O(nlogn).
- Space complexity: O(logn), that is, the space cost of recursive use of stack space.
5, Turn over the linked list in groups of K (25)
Title Description:
Give you a linked list. Each group of k nodes will be flipped. Please return to the flipped linked list.
k is a positive integer whose value is less than or equal to the length of the linked list.
If the total number of nodes is not an integer multiple of k, keep the last remaining nodes in the original order.
Advanced:
Can you design an algorithm that uses only constant extra space to solve this problem?
You can't just change the value inside the node, but you need to actually exchange nodes.
Example:
Input: head = [1,2,3,4,5], k = 2 Output:[2,1,4,3,5] Input: head = [1,2,3,4,5], k = 1 Output:[1,2,3,4,5]
Solution:
You need to group the linked list nodes in groups of k, so you can use a pointer head to point to the head nodes of each group in turn. This pointer moves forward k steps at a time until the end of the linked list. For each group, we first judge whether its length is greater than or equal to k. If so, we will flip this part of the linked list, otherwise we don't need to flip it. The idea and method of reversing the linked list are the same as before.
For a sub linked list, in addition to flipping itself, you also need to connect the head of the inverted sub linked list with the previous sub linked list, and the tail of the sub linked list with the next sub linked list, as shown in the following figure:
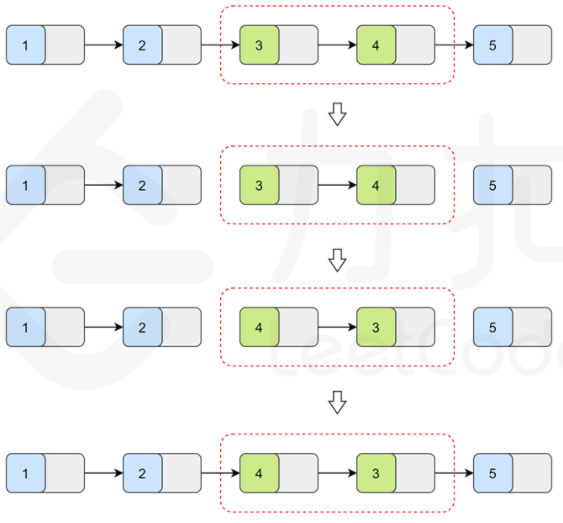
Therefore, when turning over the rotor linked list, we need not only the sub chain header node head, but also the previous node pre with head, so as to connect the sub linked list back to the pre after turning over. Similarly, we also need a node to save the next node of the linked list to be reversed, so as to connect the sub linked list back to the original linked list after reversing.
However, for the first child linked list, there is no node pre in front of its head node. Therefore, create a new node hair, connect it to the head of the linked list, and make hair as the initial value of pre, so that there is a node in front of the head.
Repeatedly move the pointers head and pre to flip the sub linked list pointed to by head until the end.
For the final return result, the defined hair is connected to the front of the head node at the beginning, and the next pointer of hair will point to the correct head node whether the linked list is flipped or not. So just return the next node of hair.
The whole idea of illustration:
Suppose k==2



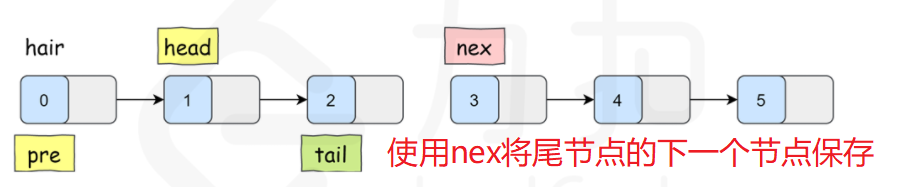

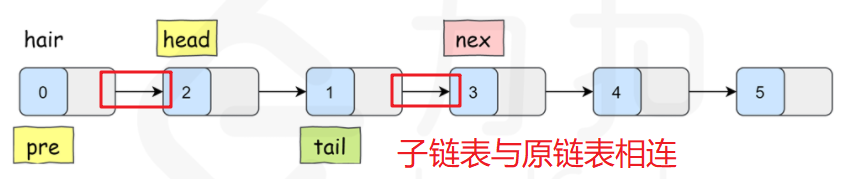
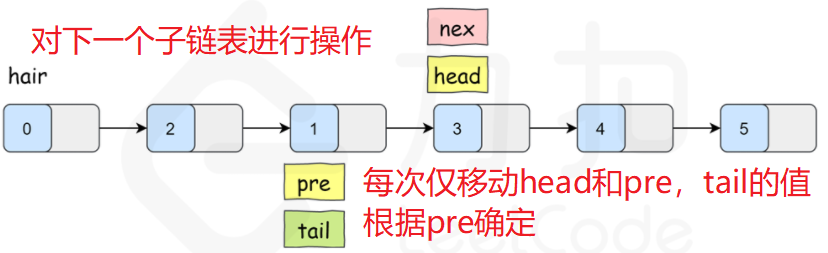
Note: the value of tail is determined according to pre, which is determined after each exchange, and then the tail can be determined.
Code implementation:
class Solution {
public ListNode reverseKGroup(ListNode head, int k) {
ListNode hair = new ListNode(); //Create virtual head node
hair.next = head;
ListNode pre = hair; //pre becomes the previous node of head
//At first, only pre was confirmed
while (head != null) {
ListNode tail = pre; //Tail indicates the tail node of the linked list to be reversed. It starts with the previous node of head
//Check whether the length of the remaining part of the node with head is greater than or equal to k
//And move the tail to the tail node of the linked list to be reversed
for (int i = 0; i < k; ++i) {
tail = tail.next;
//The tail will become the tail node of the linked list to be reversed, so the length is determined according to the tail
if (tail == null) {
return hair.next;
}
}
//At the beginning, the tail must be the previous node of the head. Only in this way can the tail become the tail node of the linked list to be reversed after moving k times. If the tail==head at the beginning, the tail will become the next node of the tail node of the linked list to be reversed after moving k times
ListNode nex = tail.next; //Keep the last node of the tail node of the linked list to be reversed to prevent disconnection
//Next, start reversing the linked list of head → tail and call the previous method of reversing the linked list
//The return value of the inversion method becomes head, and the inverted tail is the head without inversion
//So save the head without inversion
ListNode temp = head;
head = reverseList(head, tail); //The inverted head node is head
tail = temp; //The inverted tail is the head without inversion
//Reconnect the sub linked list to the original linked list
pre.next = head;
tail.next = nex;
//Move pre and head to the next set of linked lists to be reversed
pre = tail;
head = nex;
}
return hair.next;
}
//Inversion method
//The only function of the second parameter is to determine the critical value of the last node, and the idea is still the same as before
public ListNode reverseList(ListNode head, ListNode tail) {
//Recursion proceeds to the last node
if(head == tail) {
return head;
}
//Cur is the last node, and the value of cur will not change
//When head is the penultimate node, the last recursive return is the last node
ListNode cur = reverseList(head.next, tail);
//4.next.next = 4; Represents 5 to 4
head.next.next = head;
//Prevent 5 and 4 from forming a cycle, and it is not necessary to point 4 to 5
head.next = null;
//Each layer of recursion returns the constant cur value, that is, the last node
return cur;
}
}
Time complexity: O(n) (the tail node will walk all nodes in the linked list once), space complexity: O(1)
6, Sum of two numbers (1)
Title Description:
Given an integer array nums and a target value target, please find the two integers with sum as the target value in the array and return their array subscripts. For example:

1. Hash table
Idea:
Create a hash table, store the element values and corresponding index values of the array, traverse the array, and put the array elements and corresponding index values into the hash table. Once target - num [i] is found in the hash table, stop the traversal to get the results
Methods to understand in HashMap:
boolean containsKey(key); Judge whether there is a mapping relationship formed by this key in the hash table
Object get(key); Returns the value corresponding to this key
put(key, value); Store key value pairs in the hash table
Code implementation:
public class Solution {
public int[] twoSum(int[] numbers, int target) {
int[] result = new int[2];
HashMap<Integer, Integer> map = new HashMap<>();
for(int i = 0; i < numbers.length; i++) {
if(map.containsKey(target - numbers[i])) {
result[1] = i;
result[0] = map.get(target - numbers[i]);
return result;
}
map.put(numbers[i], i);
}
return result;
}
}
The time complexity O(n) only traverses the list containing n elements once, and each search in the table takes only O(1) time
Space complexity O(n), the additional space required depends on the number of elements stored in the hash table, which needs to store up to n elements
2. Hash table twice
Idea:
Create a hash table, traverse the array for the first time, put all elements in the array into the hash table, and traverse the array for the second time to find out whether there is a target - num [i] value in the hash table. Note: since all values will be put into the hash table for the first time, if the target value is 8, then 4 + 4 = 8, but the value of two elements needs to be 4 instead of adding twice for a 4 itself, Therefore, the value extracted from the hash table cannot be itself
Code implementation:
class Solution {
public int[] twoSum(int[] nums, int target) {
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
map.put(nums[i], i);
}
for (int i = 0; i < nums.length; i++) {
int complement = target - nums[i];
if (map.containsKey(complement) && map.get(complement) != i) {
return new int[] { i, map.get(complement) };
}
}
throw new IllegalArgumentException("No two sum solution");
}
}
The time complexity is O(n). The list containing n elements is traversed twice. Since the hash table shortens the search time to O(1), the time complexity is O(n)
Space complexity O(n), the additional space required depends on the number of elements stored in the hash table, which stores n elements
7, Sum of three (15)
Title Description:
Give you an array num containing n integers. Judge whether there are three elements a, b and c in num, so that a + b + c = 0? Please find out all triples that meet the conditions and are not repeated, as shown in the figure below:

Idea:
First, sort the given array, then fix a number in the array from scratch, traverse the remainder of the array with double pointers, and find the other two numbers that meet the conditions.
Specific process:
(1) Call arrays Sort sorts the array
(2) Use the left and right pointers to point to the left and right ends of the number after num [i], which are num [l] and num [R] respectively, to judge whether the sum of the three numbers is 0. If it is satisfied, it will be added to the result set
(3) If num [i] > 0, the sum of the three numbers must be greater than 0 (the number after num [i] must be greater than him), and the loop ends
(4) If nums[i] == nums[i - 1], repetition will occur and should be skipped (comparing I and i+1 at the end of traversal will lead to out of bounds, so compare i - 1)
(5) If the sum of three numbers sum == 0, Num [l] = = num [L + 1], the result will be repeated, l++
(6) If the sum of three numbers sum == 0, Num [R] = = num [R - 1], the result will be repeated, R –
Note: once sum == 0, L + + and R -- (execute on the basis of steps 5 and 6, and duplicate items can be skipped)
nums[i] there are two cases to be discussed. When sum == 0, there are two cases to be discussed
Code implementation:
class Solution {
public static List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> result = new ArrayList()<>;
//Judgment of special conditions
int len = nums.length;
if(nums == null || len < 3) return result;
Arrays.sort(nums); // Be sure to sort the array
for (int i = 0; i < len ; i++) { // Judge num [i] first. If it is not satisfied, there is no need to create L and R pointers
if(nums[i] > 0) break; // If the current number is greater than 0, the cycle ends
if(i > 0 && nums[i] == nums[i-1]) continue; // For weight removal, I > 0 must be required, otherwise i - 1 is out of bounds
//Defines the left and right pointers to the remaining elements
int L = i+1;
int R = len-1;
while(L < R){
int sum = nums[i] + nums[L] + nums[R];
if(sum == 0){
result.add(Arrays.asList(nums[i],nums[L],nums[R]));
while (L<R && nums[L] == nums[L+1]) L++; // duplicate removal
while (L<R && nums[R] == nums[R-1]) R--; // duplicate removal
L++;
R--;
}
else if (sum < 0) L++; // Don't forget these two judgments
else if (sum > 0) R--;
}
}
return result;
}
}

8, Circular linked list II(142)
Title Description:
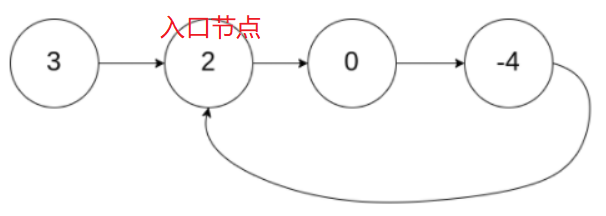
Given a linked list, return the first node from the linked list into the ring. If the linked list is acyclic, null is returned.
1. Hash table
Idea:
When traversing the node, use the hash table to record the node address. If the address is not repeated, it means that there is no ring in the linked list. If the address in the hash table is repeated, it means that there is a ring. Just return the repeated element
Code implementation:
class Solution {
public ListNode detectCycle(ListNode head) {
Set<ListNode> nodesSeen = new HashSet<>();
while (head != null) {
if (nodesSeen.contains(head)) {
return head;
} else {
nodesSeen.add(head);
}
head = head.next;
}
return null; //If there is no ring, it will jump out of the while loop
}
}
- Time complexity: O(N)
- Space complexity: O(N)
2. Speed pointer
Idea:
Use two pointers, fast and slow. They all start at the head of the linked list. Then, the slow pointer moves back one position at a time, while the fast pointer moves back two positions. If there is a ring in the linked list, the fast pointer will eventually meet the pointer in the ring again. Once fast == null, it indicates that there are no rings in the linked list, and null can be returned.
As shown in the figure below, let the length of the outer part of the link in the linked list be a. After the slow pointer enters the ring, it goes the distance of b and meets fast. Suppose that at this time, the fast pointer has completed N cycles of the ring, so its total distance is a + n(b+c) + b → a + (n+1)b +nc.
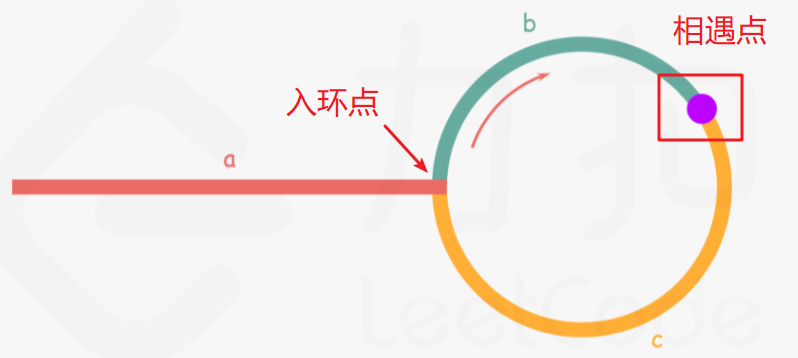
According to the meaning of the question, at any time, the distance traveled by the fast pointer is twice that of the slow pointer. Therefore, the following derivation process can be obtained:
a + (n+1)b + nc = 2(a+b) ⟹ a = c + (n−1)(b+c). (the slow pointer does not need to loop in the ring, and the first circle will meet the fast pointer)
With the above equivalent relationship, it can be found that the distance from the meeting point to the ring entry point plus the ring length of n − 1 circle is exactly equal to the distance from the head of the linked list to the ring entry point. Therefore, when slow and fast meet, an additional pointer ptr is used.
At the beginning, ptr points to the head of the linked list; Then, it and slow move backward one position at a time. After slow has gone c, the distance from ptr to the ring entrance is only a whole n - 1 circle. At this time, the slow pointer just comes to the entrance. At this time, As long as they walk the distance of N - 1 circle together, they will meet (the size of N cannot be determined. As long as they move back one position through the cycle, they will meet). Moreover, the meeting point is just the entrance and return to the node pointed by ptr.
Code implementation:
public class Solution {
public ListNode detectCycle(ListNode head) {
if (head == null) {
return null;
}
ListNode slow = head, fast = head;
while (fast != null) { //If fast == null, there must be no ring
slow = slow.next;
if (fast.next != null) { //Prevent null pointer exceptions
fast = fast.next.next;
} else { //The next node of fast = = null, there must be no ring
return null;
}
//The ptr pointer is defined when the fast and slow pointers meet
if (fast == slow) {
ListNode ptr = head;
//ptr moves one position backward with the slow pointer
while (ptr != slow) {
ptr = ptr.next;
slow = slow.next;
}
//ptr meets the slow pointer and returns ptr
return ptr;
}
}
return null;
}
}

9, Circular linked list (141)
Title Description:
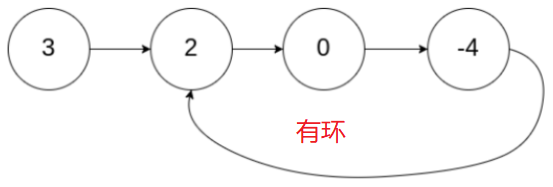
Given a linked list, judge whether there are rings in the linked list, as shown in the following figure:
1. Hash table
Idea:
The idea is the same as the topic of "entry node of link in linked list". Only the return value is different and will not be repeated
Code implementation:
class Solution {
public boolean hasCycle(ListNode head) {
Set<ListNode> nodesSeen = new HashSet<>();
while (head != null) {
if (nodesSeen.contains(head)) {
return true;
} else {
nodesSeen.add(head);
}
head = head.next;
}
return false; //If there is no ring, the while loop will jump out
}
}
2. Speed pointer
See the topic "entry node of link in linked list" for ideas and code implementation. Only the return values are different and will not be repeated.
Note: after the fast and slow pointers meet, they can return true. There is no need to define a new node to move with the slow pointer.
public class Solution {
public boolean hasCycle(ListNode head) {
if (head == null) {
return false;
}
ListNode slow = head, fast = head;
while (fast != null) { //fast == null, there must be no ring
slow = slow.next;
if (fast.next != null) { //Prevent null pointer exceptions
fast = fast.next.next;
} else { //The next node of fast = = null, there must be no ring
return false;
}
//When the fast and slow pointers meet, it indicates that there is a ring
if (fast == slow) {
return true;
}
}
return false;
}
}
10, Merge two ordered linked lists (21)
Title Description:
Merge the two ascending linked lists into a new ascending linked list and return it. The new linked list is composed of all nodes of the given two linked lists

1. Recursion
Idea:
Start from the head nodes of the two linked lists and compare the sizes in turn. The smaller nodes should point to the other nodes until the next of one party is empty. Return the nodes pointed to by the other linked list at this time (these remaining nodes must be the largest), and continue to return in turn until all nodes return successfully

Code implementation:
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
if (l1 == null) {
return l2;
}
else if (l2 == null) {
return l1;
}
else if (l1.val < l2.val) { //You can't judge L1 first Val, if l1==null, null pointer exception will occur
l1.next = mergeTwoLists(l1.next, l2);
return l1;
}
else {
l2.next = mergeTwoLists(l1, l2.next);
return l2;
}
}
}

2. Iteration
Idea:
Create a new linked list (the head node is prehead and the auxiliary node is prev). When l1 and l2 are not empty linked lists, judge which head node of the linked list has a smaller value, add the node with a smaller value to the back of prev and move prev back one bit (because the linked list cannot directly locate a node, a pointer must be used to point to the node to be operated), When a node is added to the new linked list, move the node in the corresponding linked list back one bit, and no matter which element is connected after the prev, you need to move the prev back one bit. When the cycle ends, at most one of the two linked lists is non empty, and the remaining elements must be the largest, which can be connected after the prev.
Code implementation:
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
ListNode prehead = new ListNode();
ListNode prev = prehead;
while (l1 != null && l2 != null) {
if (l1.val <= l2.val) {
prev.next = l1;
l1 = l1.next;
} else {
prev.next = l2;
l2 = l2.next;
}
prev = prev.next;
}
prev.next = l1 == null ? l2 : l1; // Be sure to add the remaining elements after prev
return prehead.next;
}
