1, Introduction
Master L. Peter Deutsch said: to iterate is human, to recurse, divide. There is no doubt that recursion is a wonderful way of thinking. For some simple recursive problems, we are always amazed at the ability of recursion to describe the problem and the simplicity of writing code, but it is not easy to truly understand the essence of recursion and flexibly use the idea of recursion to solve the problem.
Recursion: you open the door in front of you and see another door in the house. You walk over and find that the key in your hand can still open it. You open the door and find that there is another door inside. You continue to open it. Several times later, when you open the door in front of you, you find that there is only one room and no door. Then, you start to return the same way. Every time you go back to a room, you count once. When you get to the entrance, you can answer how many doors you opened with this key.
Cycle: you open the door in front of you and see another door in the house. You walk over and find that the key in your hand can still open it. You open the door and find that there is another door inside (if the front two doors are the same, then this door is the same as the front two doors; if the second door is smaller than the first door, then this door is smaller than the second door. You continue to open this door until you open all the doors. However, the people at the entrance can't wait for you to go back and tell him the answer.
The above metaphor vividly expounds the connotation of recursion and loop, so let's think about the following questions: what is recursion?
What is the essence of recursion?
What is the difference between recursion and loop?
When should I use recursion?
What should we pay attention to when using recursion?
What classical problems does recursion solve?
These problems are the problems that the author intends to elaborate in this paper.
2, Connotation of recursion
1. Definition (what is recursion?)
In mathematics and computer science, recursive (Recursion) is the way to use functions in the definition of functions. In fact, recursion, as its name implies, contains two meanings: recursive and recursive, which is the essence of recursive thinking.
2. The connotation of recursion (what is the essence of recursion?)
As in the scenario described above, recursion means going (passing) and returning (returning), as shown in the figure below It means that the recursive problem must be decomposed into several small-scale sub problems with the same form as the original problem. These sub problems can be solved with the same problem-solving ideas, just as the key in the above example can open the locks on all the back doors; "return" It means that the evolution process of these problems is a process from large to small, from near to far, and there will be a clear end point (critical point). Once the critical point is reached, there is no need to go to smaller and farther places. Finally, from this critical point, the original path returns to the origin and the original problem is solved.
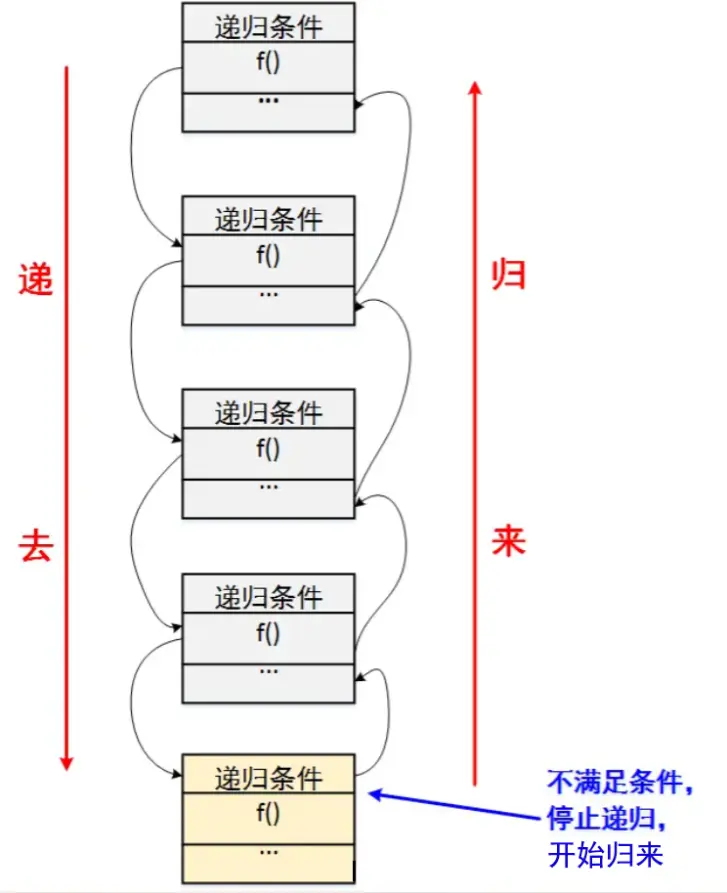
More directly, the basic idea of recursion is to transform a large-scale problem into a small-scale similar subproblem to solve. In particular, in the implementation of a function, because the method to solve a large problem and the method to solve a small problem are often the same method, a function calls itself, which is the definition of recursion. What is particularly important is this The function to solve the problem must have an explicit end condition, otherwise it will lead to infinite recursion.
3. Understanding recursion by induction
Mathematics is not bad. Our first reaction is what the mathematical model of recursion is. After all, we are better at mathematical modeling of problems than code modeling. Observing recursion, we will find that the mathematical model of recursion is actually mathematical induction, which is the most commonly used in high school series. Let's recall the mathematical induction.
Mathematical induction is applicable to transform the original problem solved into its subproblem, and its subproblem becomes the subproblem of the subproblem, and we find that these problems are actually a model, that is, there are the same logical induction processing items. Of course, there is one exception, that is, the processing method at the end of induction is not applicable to our induction processing items Of course, it can't be applied, otherwise we will have infinite induction. In general, induction mainly includes the following three key elements:
Step expression: an expression that transforms a problem into a subproblem
End condition: when can I stop using step expressions
Direct solution expression: an expression that can directly calculate the return value under the end condition
In fact, this is why recursion can be used to solve some mathematical sequence problems by programming, such as the famous Fibonacci sequence problem.
4. Three elements of recursion
After we understand the basic idea of recursion and its mathematical model, how can we write a beautiful recursive program? The author believes that we mainly grasp the following three aspects:
//1. Explicit recursive termination conditions; //2. The processing method of recursive termination is given; //3. Extract duplicate logic and reduce the scale of the problem. Copy code
1) . specify recursive termination conditions
We know that recursion is going and returning. In this case, there must be a clear critical point. Once the program reaches this critical point, it does not need to continue to pass down, but starts to return. In other words, the critical point is a simple situation that can prevent infinite recursion.
2) . give the handling method of recursive termination
We just said that there is a simple situation at the critical point of recursion. In this simple situation, we should directly give the solution to the problem. Generally, in this situation, the solution to the problem is intuitive and easy.
3) . extract duplicate logic and reduce the scale of the problem*
When expounding the connotation of recursion, we said that the recursion problem must be decomposed into several small-scale sub problems with the same form as the original problem, which can be solved with the same problem-solving ideas. From the perspective of program implementation, we need to abstract a clean and repeated logic in order to solve the sub problems in the same way.
5. Programming model of recursive algorithm
After clarifying the three elements of recursive algorithm design, we need to start writing specific algorithms. When writing algorithms, without losing generality, we give two typical recursive algorithm design models, as shown below.
Model 1: solving problems in the process of delivery
function recursion(large-scale){ if (end_condition){
// Explicit recursive termination condition end;
// Simple scenario
}else{
// In each step of converting the problem into a sub problem, solve the problem of the remaining part of the step;
// Delivery recursion (small scale)// Deliver it to the deepest place and return}8
}
Copy code
Model 2: solving problems in the process of returning
function recursion(large-scale){
if (end_condition){
// Explicit recursive termination condition end;
// Simple scenario
}else{
// First, expand the problem description, and then "return" at the end to solve the problem recurrence (small-scale) of the remaining part in each step in turn;
// Pass to solve;
// Return
} }
Copy code
6. Recursive application scenarios
In our actual learning work, recursive algorithms are generally used to solve three types of problems:
(1) The problem is defined recursively (Fibonacci function, factorial,...);
(2) The solution of the problem is recursive (some problems can only be solved by recursive methods, such as Hanoi Tower problem,...);
(3) The data structure is recursive (linked list, tree and other operations, including tree traversal, tree depth,...).
In the following, we will give some classic application cases of recursive algorithm, which basically belong to the category of the third type of problem.
3, Recursion and loop
Recursion and loop are two different typical ideas to solve problems. Recursion usually directly describes the solution process of a problem, so it is also the easiest way to think of a solution. Loop actually has the same characteristics as recursion, that is, doing repetitive tasks, but sometimes the algorithm using loop does not clearly describe the problem-solving steps. In terms of algorithm design alone, recursion and loop have no advantages or disadvantages. However, in practical development, because of the cost of function calls, recursion often brings performance problems, especially when the solution scale is uncertain; Because loops have no function call overhead, they are more efficient than recursion. Recursive solution and loop solution are often interchangeable, that is, if you can easily use loop replacement where recursion is used without affecting the reading of the program, it is often good to replace with loop. It generally needs two steps to convert the recursive implementation of the problem into a non recursive implementation: (1) establish a "stack (some local variables)" to save these contents in order to replace the system stack, such as three non recursive traversal methods of the tree;
(2) . turn the call to recursion into loop processing.
In particular, in the following, we will give some classic application cases of recursive algorithm. For the implementation of these cases, we will generally give recursive and non recursive solutions for readers to understand.
4, Classic recursive problem practice
- The first kind of problem: the problem is defined recursively
(1) 3. Factorial
/**
* Title: Realization of factorial
* Description:
* Recursive solution
* Non recursive solution
* @author rico
*/
public class Factorial {
/**
* @description Recursive implementation of factorial
* @author rico
* @created 2017 8:45:48 PM, May 10, 2014
* @param n
* @return
*/
public static long f(int n){
if(n == 1) // Recursive termination condition
return 1; // Simple scenario
return n*f(n-1); // Repeat the same logic to reduce the scale of the problem
}
--------------------------------I am the dividing line-------------------------------------
/**
* @description Non recursive implementation of factorial
* @author rico
* @created 2017 May 10, 2008 8:46:43 PM
* @param n
* @return
*/
public static long f_loop(int n) {
long result = n;
while (n > 1) {
n--;
result = result * n;
}
return result;
}
}
Copy code
(2) Fibonacci sequence
Title: Fibonacci sequence
Description: Fibonacci sequence, also known as golden section sequence, refers to such a sequence: 1, 1, 2, 3, 5, 8, 13, 21
Mathematically, Fibonacci sequence is defined recursively as follows: F0=0, F1=1, Fn=F(n-1)+F(n-2) (N > = 2, N ∈ N *).
Two recursive methods: classical method and optimization method
Two non recursive methods: recursive method and array method
* @author rico
*/
public class FibonacciSequence {
/**
* @description Classical recursive method
*
* The Fibonacci sequence is as follows:
*
* 1,1,2,3,5,8,13,21,34,...
*
* *Then, when calculating fib(5), you need to calculate FIB (4), FIB (3) and fib(2) once, and call fib(1) * twice, that is:
*
* fib(5) = fib(4) + fib(3)
*
* fib(4) = fib(3) + fib(2) ;fib(3) = fib(2) + fib(1)
*
* fib(3) = fib(2) + fib(1)
*
* This involves a lot of repeated calculations. In fact, we only need to calculate fib(4), fib(3), fib(2) and fib(1) once,
* The later optimizeFibonacci function is optimized to reduce the time complexity to O(n)
*
* @author rico
* @created 2017 May 10, 2012 12:00:42 PM
* @param n
* @return
*/
public static int fibonacci(int n) {
if (n == 1 || n == 2) { // Recursive termination condition
return 1; // Simple scenario
}
return fibonacci(n - 1) + fibonacci(n - 2); // Repeat the same logic to reduce the scale of the problem
}
Copy code
/** * @description Optimization of classical recursive method * * The Fibonacci sequence is as follows: * * 1,1,2,3,5,8,13,21,34,... * * Well, we can look at it this way: fib(1,1,5) = fib(1,2,4) = fib(2,3,3) = 5 * * That is, to 1,1 The fifth term of the Fibonacci sequence begins with 1,2 The fourth term of the Fibonacci sequence at the beginning, * And with 1,2 The fourth term of the Fibonacci sequence begins with 2,3 The third term of the Fibonacci sequence at the beginning, * More directly, we can do it in one step: fib(2,3,3) = 2 + 3 = 5,End of calculation. * * Note that the first two parameters are the first two items of the sequence, and the third parameter is the first item of the sequence we want to find. * Copy code
* Time complexity: O(n)
*
* @author rico
* @param first The first term of the sequence
* @param second The second term of the sequence
* @param n Target item
* @return
*/
public static int optimizeFibonacci(int first, int second, int n) {
if (n > 0) {
if(n == 1){ // Recursive termination condition
return first; // Simple scenario
}else if(n == 2){ // Recursive termination condition
return second; // Simple scenario
}else if (n == 3) { // Recursive termination condition
return first + second; // Simple scenario
}
return optimizeFibonacci(second, first + second, n - 1); // Repeat the same logic to reduce the scale of the problem
}
return -1;
}
--------------------------------I am the dividing line-------------------------------------
/**
* @description Non recursive solution: there is no return
* @author rico
* @created 2017 May 10, 2012 12:03:04 PM
* @param n
* @return
*/
public static int fibonacci_loop(int n) {
if (n == 1 || n == 2) {
return 1;
}
int result = -1;
int first = 1; // Maintain your own "stack" for status backtracking
int second = 1; // Maintain your own "stack" for status backtracking
for (int i = 3; i <= n; i++) { // loop
result = first + second;
first = second;
second = result;
}
return result;
}
--------------------------------I am the dividing line-------------------------------------
/**
* @description Using arrays to store Fibonacci sequences
* @author rico
* @param n
* @return
*/
public static int fibonacci_array(int n) {
if (n > 0) {
int[] arr = new int[n]; // Use temporary arrays to store Fibonacci sequences
arr[0] = arr[1] = 1;
for (int i = 2; i < n; i++) { // Assign values to temporary arrays
arr[i] = arr[i-1] + arr[i-2];
}
return arr[n - 1];
}
return -1;
}
}
Copy code
(3) . value of Yang Hui triangle
/** * @description Recursively obtain the values of the specified rows and columns (starting from 0) of Yang Hui triangle * Note: it has nothing to do with whether to create Yang Hui triangle
* @author rico
* @x Specify row
* @y Specify column
*/
/**
* Title: Yang Hui triangle is also called Pascal triangle. Its i+1 line is the coefficient of the expansion of (a+b)i.
* One of its important properties is that each number in a triangle is equal to the sum of the numbers on its two shoulders.
*
* For example, the first four rows of Yang Hui triangle are given below:
* 1
* 1 1
* 1 2 1
* 1 3 3 1
* @description Recursively obtain the values of the specified row and column (starting from 0) of Yang Hui triangle
* Note: it has nothing to do with whether to create Yang Hui triangle
* @author rico
* @x Specify row
* @y Specify column
*/
public static int getValue(int x, int y) {
if(y <= x && y >= 0){
if(y == 0 || x == y){ // Recursive termination condition
return 1;
}else{
// Recursive call to reduce the scale of the problem
return getValue(x-1, y-1) + getValue(x-1, y);
}
}
return -1;
}
}
Copy code
(4) . judgment of palindrome string
Title: judgment of palindrome string
Description: palindrome string is a string with the same forward and backward reading. For example, "98789" and "abccba" are palindrome strings
Two solutions:
Recursive judgment;
Cyclic judgment;
* @author rico
*/
public class PalindromeString {
/**
* @description Recursively determine whether a string is a palindrome string
* @author rico
* @created 2017 5:45:50 PM, May 10
* @param s
* @return
*/
public static boolean isPalindromeString_recursive(String s){
int start = 0;
int end = s.length()-1;
if(end > start){ // Recursive termination condition: two pointers move towards each other. When start exceeds end, the judgment is completed
if(s.charAt(start) != s.charAt(end)){
return false;
}else{
// Recursive call to reduce the scale of the problem
return isPalindromeString_recursive(s.substring(start+1).substring(0, end-1));
}
}
return true;
}
--------------------------------I am the dividing line-------------------------------------
/**
* @description Circular judgment palindrome string
* @author rico
* @param s
* @return
*/
public static boolean isPalindromeString_loop(String s){
char[] str = s.toCharArray();
int start = 0;
int end = str.length-1;
while(end > start){ // Loop termination condition: the two pointers move towards each other. When start exceeds end, the judgment is completed
if(str[end] != str[start]){
return false;
}else{
end --;
start ++;
}
}
return true;
}
}
Copy code
(5) . full arrangement of strings
Recursive solution
@description select one element at a time from the string array as the first element in the result; Then, arrange all the remaining elements
* @author rico
* @param s
* Character array
* @param from
* Starting subscript
* @param to
* Termination subscript
*/
public static void getStringPermutations3(char[] s, int from, int to) {
if (s != null && to >= from && to < s.length && from >= 0) { // Boundary condition check
if (from == to) { // Recursive termination condition
System.out.println(s); // Print results
} else {
for (int i = from; i <= to; i++) {
swap(s, i, from); // Exchange prefixes as the first element in the result, and then arrange all the remaining elements
getStringPermutations3(s, from + 1, to); // Recursive call to reduce the scale of the problem
swap(s, from, i); // Replace the prefix and restore the character array
}
}
}
}
/**
* @description Exchange the specified characters in the character array
* @author rico
* @param s
* @param from
* @param to
*/
public static void swap(char[] s, int from, int to) {
char temp = s[from];
s[from] = s[to];
s[to] = temp;
}
Copy code
Non recursive solution (dictionary order)
Title: non recursive algorithm for full arrangement of strings (full arrangement of dictionary order)
Description: the dictionary is arranged in full order. Its basic idea is:
First, sort the strings to be arranged in a dictionary, that is, get the smallest arrangement in the whole arrangement
Then, find the smallest permutation larger than it, and repeat this step until the maximum value is found, that is, the inverse sequence of dictionary sorting
You don't need to care about string length
@author rico
public class StringPermutationsLoop {undefined
/**
* @description Dictionary order complete arrangement
*
* Set a string(Character array)The full arrangement of n Two, respectively A1,A2,A3,...,An
*
* 1. Find the smallest permutation Ai
* 2. Find a ratio Ai Large minimum successor arrangement Ai+1
* 3. Repeat the previous step until there is no such successor
*
* The point is how to find a direct successor to the arrangement:
* For Strings(Character array)a0a1a2......an,
* 1. from an reach a0 Find the first two characters in ascending order(Namely ai < ai+1),that ai+1 Is an extreme value because ai+1 The following characters are arranged in descending order top=i+1;
* 2. from top place(include top)Start search ratio ai Large minimum value aj,remember minMax = j;
* 3. exchange minMax Chu he top-1 Character at;
* 4. Flip top Characters after(include top),That is, the direct successor arrangement of an arrangement is obtained
*
Copy code
* @author rico
* @param s
* Character array
* @param from
* Starting subscript
* @param to
* Termination subscript
*/
public static void getStringPermutations4(char[] s, int from, int to) {
Arrays.sort(s,from,to+1); // All elements of the character array are arranged in ascending order to obtain the minimum arrangement
System.out.println(s);
char[] descendArr = getMaxPermutation(s, from, to); // The inverse sequence of the maximum permutation, that is, the minimum permutation, is obtained
while (!Arrays.equals(s, descendArr)) { // Loop termination condition: iteration to maximum permutation
if (s != null && to >= from && to < s.length && from >= 0) { // Boundary condition check
int top = getExtremum(s, from, to); // Find the extreme value of the sequence
int minMax = getMinMax(s, top, to); // Find the position of the minimum value larger than s[top-1] from top (including top)
swap(s, top - 1, minMax); // Swap characters at minMax and top-1
s = reverse(s, top, to); // Flip characters after top
System.out.println(s);
}
}
}
/**
* @description Exchange the specified characters in the character array
* @author rico
* @param s
* @param from
* @param to
*/
public static void swap(char[] s, int from, int to) {
char temp = s[from];
s[from] = s[to];
s[to] = temp;
}
/**
* @description Get the extreme value of the sequence
* @author rico
* @param s sequence
* @param from Starting subscript
* @param to Termination subscript
* @return
*/
public static int getExtremum(char[] s, int from, int to) {
int index = 0;
for (int i = to; i > from; i--) {
if (s[i] > s[i - 1]) {
index = i;
break;
}
}
return index;
}
/**
* @description Find the position of the minimum value larger than s[top-1] from top
* @author rico
* @created 2017 9:21:13 am, May 10
* @param s
* @param top Location of maximum
* @param to
* @return
*/
public static int getMinMax(char[] s, int top, int to) {
int index = top;
char base = s[top-1];
char temp = s[top];
for (int i = top + 1; i <= to; i++) {
if (s[i] > base && s[i] < temp) {
temp = s[i];
index = i;
}
continue;
}
return index;
}
/**
* @description Sequence after flipping top (including top)
* @author rico
* @param s
* @param from
* @param to
* @return
*/
public static char[] reverse(char[] s, int top, int to) {
char temp;
while(top < to){
temp = s[top];
s[top] = s[to];
s[to] = temp;
top ++;
to --;
}
return s;
}
/**
* @description The maximum arrangement is obtained according to the minimum arrangement
* @author rico
* @param s Minimum arrangement
* @param from Starting subscript
* @param to Termination subscript
* @return
*/
public static char[] getMaxPermutation(char[] s, int from, int to) {
//Copies the smallest permutation to a new array
char[] dsc = Arrays.copyOfRange(s, 0, s.length);
int first = from;
int end = to;
while(end > first){ // Cycle termination condition
char temp = dsc[first];
dsc[first] = dsc[end];
dsc[end] = temp;
first ++;
end --;
}
return dsc;
}
Copy code
(6) 2. Binary search
@description Recursive implementation of binary search
@author rico
@param array target array
@param low Left boundary
@param high Right boundary
@param target target value
@return Target value location
public static int binarySearch(int[] array, int low, int high, int target) {
//Recursive termination condition
if(low <= high){
int mid = (low + high) >> 1;
if(array[mid] == target){
return mid + 1; // Returns the location of the target value, starting with 1
}else if(array[mid] > target){
// Since array[mid] is not the target value, it can be excluded when searching recursively again
return binarySearch(array, low, mid-1, target);
}else{
// Since array[mid] is not the target value, it can be excluded when searching recursively again
return binarySearch(array, mid+1, high, target);
}
}
return -1; //Indicates that no search was found
}
--------------------------------I am the dividing line-------------------------------------
/**
* @description Non recursive implementation of binary search
* @author rico
* @param array target array
* @param low Left boundary
* @param high Right boundary
* @param target target value
* @return Target value location
*/
public static int binarySearchNoRecursive(int[] array, int low, int high, int target) {
// loop
while (low <= high) {
int mid = (low + high) >> 1;
if (array[mid] == target) {
return mid + 1; // Returns the location of the target value, starting with 1
} else if (array[mid] > target) {
// Since array[mid] is not the target value, it can be excluded when searching recursively again
high = mid -1;
} else {
// Since array[mid] is not the target value, it can be excluded when searching recursively again
low = mid + 1;
}
}
return -1; //Indicates that no search was found
}
Copy code
- The second kind of problem: the solution of the problem is realized by recursive algorithm
(1) The tower of Hanoi
Title: Hanoi Tower problem
Description: there was A Vatican Pagoda in ancient times. There were three seats A, B and C in the pagoda. There were 64 plates on seat A. the plates were of different sizes, the large ones were below and the small ones were above.
A monk wanted to move the 64 plates from seat a to seat C, but only one plate can be moved at a time. During the movement, the plates on the three seats always keep the big plate under,
The small disc is on the. B seat can be used during movement. It is required to input the number of layers and output how each step moves after operation.
* @author rico
*/
public class HanoiTower {
/**
* @description In the program, we call the top plate the first plate and the bottom plate the nth plate
* @author rico
* @param level: Number of plates
* @param from Initial address of the plate
* @param inter Used for transfer when transferring plates
* @param to Destination address of the plate
*/
public static void moveDish(int level, char from, char inter, char to) {
if (level == 1) { // Recursive termination condition
System.out.println("from" + from + " Moving plate" + level + " No. to" + to);
} else {
// Recursive call: move level-1 plates from from to inter (not a one-time move, only one plate can be moved at a time, where to is used for turnover)
moveDish(level - 1, from, to, inter); // Recursive call to reduce the scale of the problem
// Move the level plate from seat A to seat C
System.out.println("from" + from + " Moving plate" + level + " No. to" + to);
// Recursive call: move level-1 plates from inter to from for turnover
moveDish(level - 1, inter, from, to); // Recursive call to reduce the scale of the problem
}
}
public static void main(String[] args) {
int nDisks = 30;
moveDish(nDisks, 'A', 'B', 'C');
}
Copy code
- The third kind of problem: the structure of data is defined recursively
(1) . binary tree depth
Title: recursively solving the depth of binary tree
Description:
@author rico
@created 2017 6 p.m. on May 8:34:50
public class BinaryTreeDepth {
/**
* @description Returns the depth of a binary number
* @author rico
* @param t
* @return
*/
public static int getTreeDepth(Tree t) {
// The tree is empty
if (t == null) // Recursive termination condition
return 0;
int left = getTreeDepth(t.left); // Recursively find the depth of the left subtree to reduce the scale of the problem
int right = getTreeDepth(t.left); // Recursively find the depth of the right subtree to reduce the scale of the problem
return left > right ? left + 1 : right + 1;
}
}
Copy code
(2) . binary tree depth
@description Preorder traversal(recursion)
@author rico
@created 2017 May 22, 2003 3 p.m:06:11
@param root
@return
public String preOrder(Node<E> root) {
StringBuilder sb = new StringBuilder(); // Save to recursive call stack
if (root == null) { // Recursive termination condition
return ""; // ji
}else { // Recursive termination condition
sb.append(root.data + " "); // The preamble traverses the current node
sb.append(preOrder(root.left)); // Preorder traversal of left subtree
sb.append(preOrder(root.right)); // Preorder traversal right subtree
return sb.toString();
}
}
Copy code
last
If you think this article is a little helpful to you, give it a compliment. Or you can join my development exchange group: 1025263163 learn from each other, and we will have professional technical Q & A to solve doubts
If you think this article is useful to you, please click star: http://github.crmeb.net/u/defu esteem it a favor!