Analysis of algorithm design principle
Quick sort is an improvement on bubble sort. The basic idea of quick sort is to divide the data to be sorted into two independent parts through one-time sorting, in which all the data in one part is smaller than all the data in the other part, and then quickly sort the two fractional data respectively according to this method. The whole sorting process can be recursive, Make the whole data into an ordered sequence.
The basic steps are as follows: 1) first take a number from the number sequence as the reference number; 2) In the partition process, all numbers larger than this number are placed on its right, and all numbers less than or equal to it are placed on its left. 3) Repeat the second step for the left and right intervals until there is only one number in each interval.
The non recursive implementation method requires that the function call part in the recursive implementation be changed into the calling function in the iteration. Here we can use the queue or stack to save the beginning position and the ending position in each recursion, so that we can jump off a set of start and end position subscript from the queue or stack after the end of each fast row, and then make quick row. Stop until the queue or stack is empty. I use the stack to save the start and end positions. Each time, the left quick row is performed first. Therefore, when stacking the positions, first push the start and end mark positions on the right into the stack, and then push the left into the stack
2. Programming
Recursive implementation:
#include<stdio.h>
#include<stdlib.h>
void QuickSort_GetKey(double *p,int len);
void QuickSort_Recursion(double *p,int len);
int main()
{
int i;
double arr[]={-34,4,0,6000.354,5.43,-343.23};
int n=sizeof(arr)/sizeof(double);
printf("The array before sorting is:\n");
for(i=0;i<n;i++)
printf("%lf ",arr[i]);
QuickSort_Recursion(arr,n);
printf("\n The array after quick sorting is:\n");
for(i=0;i<n;i++)
printf("%lf ",arr[i]);
return 0;
}
void QuickSort_Recursion(double *p,int len) //A quick sort algorithm function that defines a recursive method
{
int i=0,j=len-1;
QuickSort_GetKey(p,len-1);
if(len<=1)
return;
double key=p[j]; //Select a key as the pivot
while(i<j)
{
while(i<j&&p[i]<key)
{
i++;
}
p[j]=p[i];
while(i<j&&p[j]>key)
{
j--;
}
p[i]=p[j];
}
p[i]=key;
QuickSort_Recursion(p,j); //Quick sort the previous subarray
QuickSort_Recursion(p+j+1,len-j-1); //Quick sort the latter subarray
}
void QuickSort_GetKey(double *p,int len) //Define the function of finding the hub. Take the median of the first, middle and last three numbers as the hub and put it at the end
{
int tem;
if(p[0]>p[len/2])
{
tem=p[0];
p[0]=p[len/2];
p[len/2]=tem;
}
if(p[0]>p[len])
{
tem=p[0];
p[0]=p[len];
p[len]=tem;
}
if(p[len/2]<p[len])
{
tem=p[len/2];
p[len/2]=p[len];
p[len]=tem;
}
}Non recursive implementation:
#include<stdio.h>
#include<stdlib.h>
void quickSort(int *arr, int size);
int QuickSort_Getposition(int *arr, int begin, int end);
typedef struct Stack //Define structure stack
{
int *data;
int size;
}stack;
void InitStack(stack *s) //Initialization stack
{
int *data = (int*)malloc(20 * sizeof(int)); //Apply to open up an array space with a length of 20
if (data == NULL) //If the application cannot be found, an error will be reported and you will exit
{
return;
}
s->data = data;
s->size = 0;
}
void PushStack(stack *s,int d) //Stack function
{
if (s->size > 20) //If the stack is full, return
{
return;
}
else
s->data[s->size++] = d;
}
void PopStack(stack *s) //Out of stack function
{
if (s->size == 0) //If there is no data in the stack, it will be returned
{
return;
}
else
s->size--;
}
int TopStack(stack *s) //Display the contents at the end of the stack
{
return s->data[s->size-1];
}
int EmptyStack(stack *s) //Function to determine whether the stack is empty
{
return(s->size==0);
}
void Print(int *arr, int size) //Print function
{
int i = 0;
for (i = 0; i < size; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
int MiddleNumber(int *arr, int begin, int end)
{
int mid = begin + ((end - begin) /2);
if (arr[begin] > arr[mid])
{
if (arr[begin] > arr[end])
{
if (arr[mid] > arr[end])
{
return mid;
}
else
return end;
}
else
return begin;
}
else
{
if (arr[mid] > arr[end])
{
if (arr[begin] > arr[end])
{
return begin;
}
else
{
return end;
}
}
else
return mid;
}
}
int main()
{
int arr[] = {0,5,3,2,9,8,7,6,4,1};
printf("Before sorting: "); //Print
Print(arr,sizeof(arr)/sizeof(int));
quickSort(arr,sizeof(arr)/sizeof(int));
printf("After sorting: ");
Print(arr, sizeof(arr)/sizeof(int));
return 0;
}
void quickSort(int *arr, int size) //Define quick sort non recursive implementation function
{
stack s; //Stack for storing start and end marks
int position;
int left = 0;
int right = 0;
InitStack(&s);
PushStack(&s, 0);
PushStack(&s, size);
while (!EmptyStack(&s))
{
right = TopStack(&s);
PopStack(&s);
left=TopStack(&s);
PopStack(&s);
position = QuickSort_Getposition(arr, left, right-1);
//First quickly arrange the left side of the benchmark, then put the subscript on the back side into the stack first
if ((right-left)>position+1)
{
PushStack(&s,position+1);
PushStack(&s,right-left);
}
if (position>0)
{
PushStack(&s,0);
PushStack(&s,position);
}
}
}
int QuickSort_Getposition(int *arr, int begin, int end) //Function for defining datum value (excavation method)
{
int index = MiddleNumber(arr, begin, end);
if (index != end)
{
int tem=arr[index];
arr[index]=arr[end];
arr[end]=tem;
}
//First pit
int key = arr[end];
int k = end;
while (begin != end)
{
/*begin Start from the left to find elements larger than keywords and put them into the pit
,begin The location becomes a pit*/
while (arr[begin] <= key&&begin < end)
{
begin++;
}
if (begin != end)
{
arr[end] = arr[begin];
end--;
}
/*end Start from the right, find the element smaller than the keyword and put it into the begin pit*/
while (arr[end] >= key&&begin < end)
{
end--;
}
if (begin != end)
{
arr[begin] = arr[end];
begin++;
}
}
if (begin != k)
{
arr[begin] = key;
}
return begin;
}3. Operation results
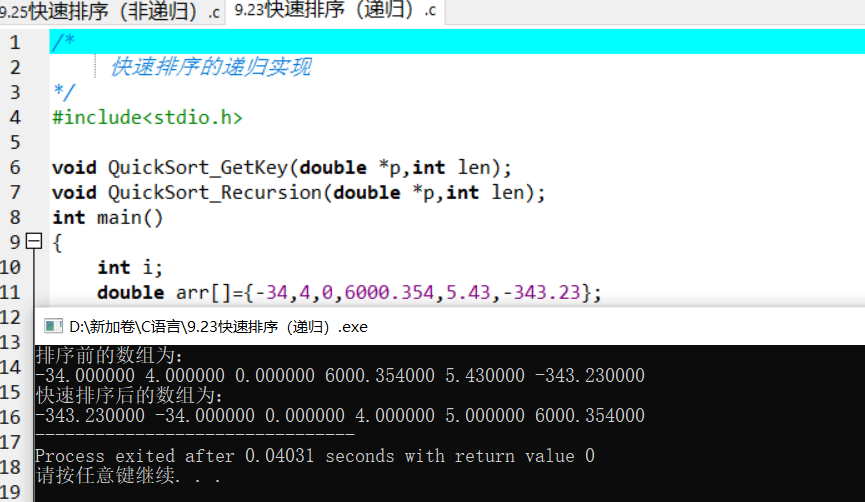
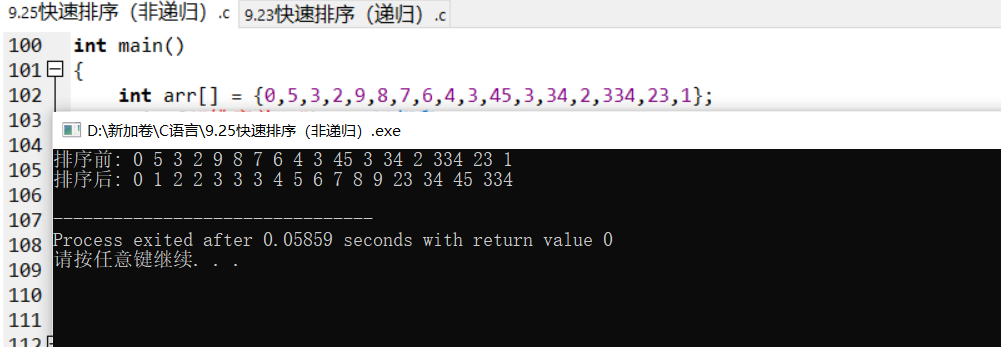
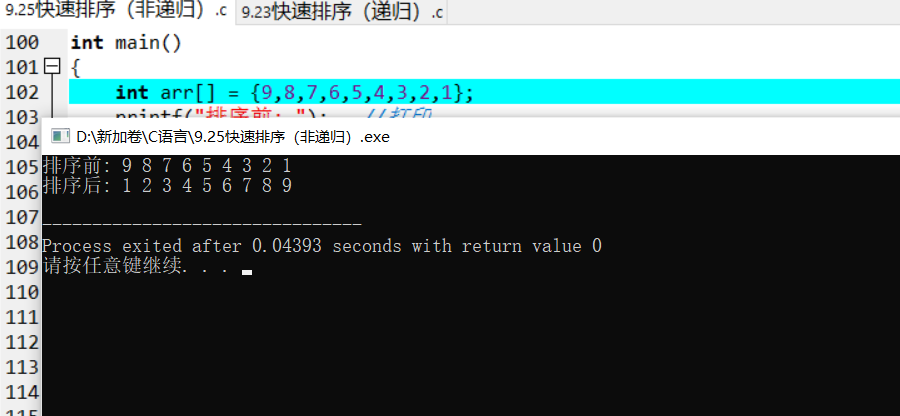
4. Algorithm analysis (complexity)
The length of fast sorting is n-times, and the main operation time is n-times. The process of quickly sorting n elements forms a recursive tree. In this recursive tree, each layer can divide up to n elements, and the time spent is O(n). When the initial sorting data is randomly distributed so that the number of elements in the two sub intervals divided into each time is roughly equal, the height of the recursive tree is log2n, and the fast sorting presents the best case, that is, the time complexity in the best case is O(nlog2n). The average time complexity of the quick sort algorithm is also O(nlog2n).
The time complexity of the non recursive implementation algorithm is the same, because the non recursive implementation process is the same as recursion. The difference is that non recursion reduces the overhead of the stack. After calling a function in each iteration, the overhead of the function on the stack is removed and a new overhead is opened up for the next function call.
5. Problem solving harvest
The worst-case time complexity of quick sort algorithm is O(n2), and the best and average time complexity are O(nlog2n). The time complexity is related to the sorting mode and benchmark value of the original array. Therefore, quick sort is an unstable algorithm. In order to make quick sort more stable, we can design some methods to find keywords. For example, when I write code, It defines a keyword that takes the median of the first, middle and last three numbers as the keyword, which can avoid the maximum or minimum keyword found each time, so as to improve the stability of fast scheduling. Of course, it can also take the random value as the keyword.