Longest palindrome string
String abcbada the longest palindrome string is abcba. The longest palindrome string ensures that the first and last characters are the same, and the substring after removing the first and last characters is also a palindrome string, such as bcb.
According to this rule, ab is not a palindrome string because the beginning and end are different. Abcbada is not a palindrome string, because even if the beginning and end are the same, its substring bcbad is not a palindrome string, so abcbada is not a palindrome string.
dynamic programming
Dynamic programming can be used to solve the length problem of the maximum palindrome string of a string. The basic idea is to list the palindrome strings with a length of 1~n in turn, and finally return the maximum length n.
The idea of dynamic programming is to find the derivation formula:
1 if the beginning and end elements are different, it is not a palindrome string.
2 if the first and last elements are the same, and the substring obtained after removing the first and last elements is still a palindrome string, the string is a palindrome string.
Assuming a string str, we write the above formula as pseudo code
1 str[begin] != str[end] be str Not a palindrome string 2 str[begin] == str[end], And str[begin+1:end-1]It's a palindrome string,be str It's a palindrome string.
We use the two-dimensional array dp[i][j] to indicate whether the string with subscripts from I to j is a palindrome string. If it is a palindrome string, dp[i][j] == 1, otherwise dp[i][j] == 0
Therefore, a palindrome string should meet the following conditions
dp[i+1][j-1] ==1 && str[i] == str[j]
When the length is 1, the string from I to I defaults to palindrome string, dp[i][i] = 1
When the length is 2, the string from I to i+1 is judged as STR [i] = = STR [i+1] -- > DP [i] [i+1] = 1
When the length is 3, for the string from I to i+2, judge STR [i] = = STR [i+2] & & DP [i + 1] [i + 1] = = 1 - > DP [i] [i+2] = 1
When the length is 4, for the string from I to i+3, judge STR [i] = = STR [i+3] & & DP [i + 1] [i + 2] = = 1 - > DP [i] [i+3] = 1
.....
After deriving the law of dp, start writing code and calculate all possible dp
int max_palindrome(string str, string &palindstr)
{
//Initialize 2D vector
vector<vector<int>> dp(str.length(), vector<int>(str.length(), 0));
int maxpalind = 0;
//First, traverse the dp with statistical length of 2 and length of 1
//Prepare for the future recurrence of dp with length n
for (size_t i = 0; i < str.length(); i++)
{
dp[i][i] = 1;
if (i + 1 >= str.length())
{
break;
}
if (str[i] == str[i + 1])
{
dp[i][i + 1] = 1;
maxpalind = 2;
}
}
//"abcdcba"
//Outer loop control length
for (int len = 3; len <= str.length(); len++)
{
//Inner loop control start position
for (int i = 0; i + len - 1 < str.length(); i++)
{
//The head and tail are the same, and the substring is still a palindrome string after removing the head and tail
if (str[i] == str[i + len - 1] && dp[i + 1][i + len - 2] == 1)
{
//Update maximum length
maxpalind = len;
//Update the dp tag, and the tag i~i+len-1 is a palindrome string
dp[i][i + len - 1] = 1;
palindstr = str.substr(i, i + len - 1);
}
}
}
return maxpalind;
}
Calculate the length from length 3 to the length of the string. The maxpalind updated last is the maximum length. There may be more than one palindrome string. Here, the last one is returned.
Test in main function
int main(){
cout << "Dynamic programming ...." << endl;
string str = "abcdcb";
string temp = "";
cout << "str is " << str << endl;
int maxlen = max_palindrome(str, temp);
cout << "max palindrome is " << temp << " size is " << maxlen << endl;
}
Program output
Dynamic programming .... str is abcdcb max palindrome is bcdcb size is 5
Center expansion method
The center expansion method can also solve the string palindrome problem. Select each element and set it as the center. If the palindrome string is satisfied, it will be expanded to the left and right in turn until the boundary is reached or the palindrome string condition is not satisfied.
As shown below
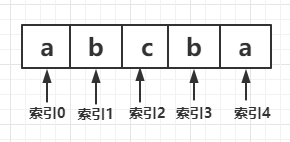
From the node with index 0 to the node with index 4, when a node is centered, judge whether its left node and right node are equal. If they are equal, the left node is left and the right node is right until the left and right nodes are unequal or the left and right nodes are boundary nodes.
give an example:
When we find node c with index 2 and judge that its left node is b and its right node is also b, then the left node moves left and points to a, and the right node moves right and points to A. at this time, the left and right nodes have reached the boundary, and the largest palindrome string abcba is found.
One problem with the above idea is that the largest palindrome string found is incorrect in the face of the following situations.
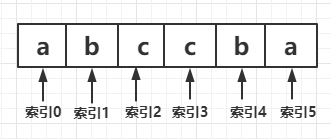
The maximum palindrome string cannot be found according to the above method, and this palindrome string exists as abccba. The problem is that when the even number of nodes are symmetrical, we cannot find the palindrome string with the node with index 2 as the center, the left node as b and the right node as c. The solution is to set index 2 as the left node and index 3 as the right node to find the palindrome string.
Therefore, the extended scheme is modified to the union of the above two algorithms
1. With a single node as the center, judge that the left and right nodes are symmetrical
2. Take the double node as the center to judge the symmetry of the left and right nodes
First, according to the equality of left and right nodes, the left node moves left and the right node moves right
int cal_maxlen(string str, int left, int right)
{
while (left >= 0 && right < str.length() && str[left] == str[right])
{
left--;
right++;
}
//Because the boundary and the left and right values are not equal, - 1 is required at this time
// Suppose the string is abcbd, then left is 0 and right is 4 = > 4-0-1 = 3
return right - left - 1;
}
The above code calculates the length of the palindrome string according to the difference of - 1 between the left and right nodes.
Next, we implement node centric traversal of the expanded logic
int center_expend(string str, string &palindstr)
{
int maxpalind = 0;
//Iterate from 0 until the end of the string
for (int i = 0; i < str.length() - 1; i++)
{
//Single node centric expansion
auto len2 = cal_maxlen(str, i, i);
//Expand with two nodes as the center
auto len1 = cal_maxlen(str, i, i + 1);
auto maxlen = 0;
len2 > len1 ? maxlen = len2 : maxlen = len1;
if (maxlen > maxpalind)
{
maxpalind = maxlen;
//The position of the left and right nodes is calculated here
//Find the starting position by halving the total length maxlen
// Suppose the string is abccba, i is 2, and maxlen is 6
//If the string is abcba,i is 2 and maxlen is 5, the following rules also apply
auto start = i - (maxlen - 1) / 2;
auto end = i + maxlen / 2;
palindstr = str.substr(start, end);
}
}
return maxpalind;
}
Next, do the test in the main function
int main(){
cout << "Center expend ...." << endl;
string str2 = "abcddcbams";
string temp2 = "";
int maxlen2 = center_expend(str2, temp2);
cout << "str2 is " << str2 << endl;
cout << "max palindrome is " << temp2 << " size is " << maxlen2 << endl;
}
Program output
Center expend .... str2 is abcddcbams max palindrome is abcddcb size is 8
summary
There is also the horse drawn cart algorithm to solve the string palindrome, which is to first insert '#' before and after each character through traversal, and then execute the center expansion algorithm to achieve o(n) complexity. I don't want to repeat here. I think it's enough to be good at solving palindrome problems through dynamic programming and center expansion algorithm.