Find the maximum and minimum values of the array

In the program, we often use an array (list) to store a given linear sequence (such as {1,2,3,4}), so how to find the maximum or minimum value in the array (sequence)?

There are many algorithms for finding the maximum or minimum value in an array (sequence). Next, we take the {3,7,2,1} sequence as an example to explain two algorithms for finding the maximum value. One is a common algorithm, and the other is solved with the help of divide and conquer algorithm.

General algorithm

The solution of ordinary algorithm is to create two variables Max and min to record the maximum and minimum values in the array respectively, and their initial values are the first number in the array. Traverse the array from the second number, and store it in the max variable every time a number larger than max is encountered; Every time a number smaller than min is encountered, it is stored in the Min variable. Until the entire array is traversed, Max records the maximum value in the array and min records the minimum value in the array.

The following animation demonstrates the process of finding the maximum value:

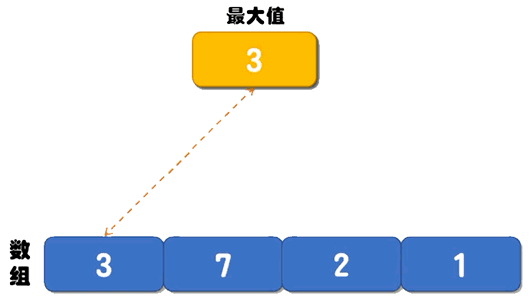
Figure 1 the process of finding the maximum value in the array
The process of finding the minimum value is similar to that in Figure 1. The specific animation demonstration will not be given here.

The following is the pseudo code corresponding to the ordinary algorithm:

input num[1...n]              // Enter n numbers
max <- num[1]                // Assign the first number to max (representing the maximum value)
min <- num[1]                // Assign the first number to min (indicating the minimum value)
for i <- 2 to n:             // Traverse from the second number
    if num[i] > max:         // If max is less than the number traversed, the value of max is updated
        max <- num[i]
    if num[i] < min:         // If min is less than the number traversed, the value of Min is updated
        min <- num[i]
Print max , min              // Output the values of max and min

The implementation process is very simple. Interested readers can write the corresponding C, Java or Python code by themselves.

Divide and conquer algorithm

The following figure shows the implementation process of finding the maximum value in {3, 7, 2, 1} with divide and conquer algorithm:

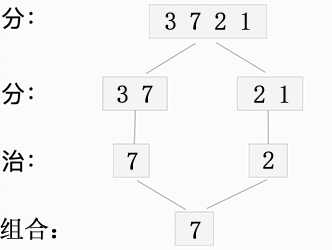
Figure 2 finding the maximum value by divide and conquer algorithm

The implementation idea of divide and conquer algorithm is to continuously divide the elements in the array until the number of elements in each group is ≤ 2. Since there are at most two elements in each group, it is easy to find the most value (maximum or minimum value) among them, and then compare these most values in pairs. Finally, the most value found is the most value in the whole array.

As shown in Figure 2, with the help of the idea of "divide and rule", we convert the problem of "finding the most value in {3,7,2,1}" into: first find out the respective most values in {3,7] and [2,1}, and then compare the found most values in pairs. Finally, we can find the most value in the whole array.

The following is the pseudo code for the divide and conquer algorithm to find the maximum value in the array:

input arr[1...n]           // Enter n numbers
arr_max(x , y) :          // Design a recursive function, [x, y] to limit the range of the maximum number
    if y-x ≤ 1 :         // If the value of y-x is less than or equal to 1, compare the values of arr[x] and arr[y], and the larger is the maximum value 
        return max(arr[x] , arr[y])
    else :
        // The [x, y] region is divided into [x, ⌊ (x+y)/2 ⌋] and [⌊ (x+y)/2+1 ⌋, y], and the maximum values in the two regions are calculated
        max1 = arr_max(x , ⌊(x+y)/2⌋ )    
        max2 = arr_max( ⌊(x+y)/2+1⌋ , y)
    return max(max1 , max2)   // Compare the maximum values of the two regions and finally find the maximum value in [x, y]

The C language program of divide and conquer algorithm for "finding the maximum value in the array" is as follows:

#include <stdio.h>
//User defined function, where [left,right] represents the range to find the maximum value in the arr array
int get_max(int* arr, int left, int right) {
    int max_left = 0, max_right = 0, middle = 0;
    //If the array does not exist
    if (arr == NULL) {
        return  -1;
    }
    //If there is only one number in the lookup range
    if (right - left == 0) {
        return arr[left];
    }
    //If there are 2 numbers in the search range, you can compare them directly
    if (right - left <= 1) {
        if (arr[left] >= arr[right]) {
            return arr[left];
        }
        return  arr[right];
    }
    //Equally divided into 2 areas
    middle = (right - left) / 2 + left;
    //Get the maximum value in the left area
    max_left = get_max(arr, left, middle);
    //Get the maximum value in the right area
    max_right = get_max(arr, middle + 1, right);
    //Compare the maximum values on the left and right sides to find the maximum value of [left,right] the whole area
    if (max_left >= max_right) {
        return  max_left;
    }
    else {
        return max_right;
    }
}
int main() {
    int arr[4] = { 3,7,2,1 };
    int max = get_max(arr, 0, 3);
    printf("Maximum:%d", max);
    return 0;
}

The Java program of divide and conquer algorithm for "finding the maximum value in the array" is as follows:

public class Demo {
    public static int get_max(int [] arr,int left,int right) {
        //If the array does not exist or there are no elements in the array
        if (arr == null || arr.length == 0) {
            return -1;
        }
        //If there are only 2 numbers in the search range, you can compare them directly
        if(right - left <=1) {
            if(arr[left] >= arr[right]) {
                return arr[left];
            }
            return arr[right];
        }
        //Equally divided into 2 areas
        int middle = (right-left)/2 + left;
        int max_left = get_max(arr,left,middle);
        int max_right = get_max(arr,middle+1,right);
        if(max_left >= max_right) {
            return max_left;
        }else {
            return max_right;
        }
    }
    public static void main(String[] args) {
        int [] arr = new int[] { 3,7,2,1 };
        int max = get_max(arr,0,3);
        System.out.println("Maximum:"+max);
    }
}

The Python program of divide and conquer algorithm for "finding the maximum value in the array" is as follows:

def get_max(arr,left,right):
    #There is no data in the list
    if len(arr) == 0:
        return -1
    #If there are only 2 numbers in the search range, you can compare them directly
    if right - left <= 1:
        if arr[left] >= arr[right]:
            return arr[left]
        return arr[right]
    #Equally divided into 2 areas
    middle = int((right-left)/2 + left)
    max_left = get_max(arr,left,middle)
    max_right = get_max(arr,middle+1,right)
    if max_left >= max_right:
        return max_left
    else:
        return max_right
arr = [3,7,2,1]
max = get_max(arr,0,3)
print("Maximum:",max,sep='')

The output results of the above procedures are:

Maximum: 7

You can write your own program to find the minimum value in the array according to the pseudo code and the program given to find the maximum value in the array, which will not be repeated here.