The establishment of binary tree and its basic traversal way:
The content of this paper's non recursive traversal method refers to
- Preorder traversal: root left and right
void PreOrder(BTtree &T)
{
if(T)
{
cout<< T->val << ' ';
PreOrder(T->left);
PreOrder(T->right);
}
}
- Middle order traversal: left root right
void InOrder(BTtree &T)
{
if(T)
{
InOrder(T->left);
cout<<T->val<<' ';
InOrder(T->right);
}
}- Backward traversal: left and right roots
void PostOrder(BTtree &T)
{
if(T)
{
PostOrder(T->left);
PostOrder(T->right);
cout<<T->val<<' ';
}
}A simpler non recursive method of traversing binary tree
Unified implementation ideas and code style methods, complete three kinds of non recursive traversal of binary tree. Refer to the blog above. The accuracy of the code has not been verified in specific cases.
//Simpler non recursive preorder traversal
void preorderTraversalNew(TreeNode *root, vector<int> &path)
{
stack< pair<TreeNode *, bool> > s;
s.push(make_pair(root, false));
bool visited;
while(!s.empty())
{
root = s.top().first;
visited = s.top().second;
s.pop();
if(root == NULL)
continue;
if(visited)
{
path.push_back(root->val);
}
else
{
s.push(make_pair(root->right, false));
s.push(make_pair(root->left, false));
s.push(make_pair(root, true));
}
}
}
//Simpler non recursive middle order traversal
void inorderTraversalNew(TreeNode *root, vector<int> &path)
{
stack< pair<TreeNode *, bool> > s;
s.push(make_pair(root, false));
bool visited;
while(!s.empty())
{
root = s.top().first;
visited = s.top().second;
s.pop();
if(root == NULL)
continue;
if(visited)
{
path.push_back(root->val);
}
else
{
s.push(make_pair(root->right, false));
s.push(make_pair(root, true));
s.push(make_pair(root->left, false));
}
}
}
//Simpler non recursive postorder traversal
void postorderTraversalNew(TreeNode *root, vector<int> &path)
{
stack< pair<TreeNode *, bool> > s;
s.push(make_pair(root, false));
bool visited;
while(!s.empty())
{
root = s.top().first;
visited = s.top().second;
s.pop();
if(root == NULL)
continue;
if(visited)
{
path.push_back(root->val);
}
else
{
s.push(make_pair(root, true));
s.push(make_pair(root->right, false));
s.push(make_pair(root->left, false));
}
}
}
- A more concise non recursive code is traversed first
void preorderTraversalNew(TreeNode *root, vector<int> &path)
{
stack<TreeNode *> s;
s.push(root);
while(!s.empty())
{
root = s.top();
s.pop();
if(root == NULL)
{
continue;
}
else
{
path.push_back(root->val);
s.push(root->right);
s.push(root->left);
}
}
}
Program example code:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <bits/stdc++.h>
using namespace std;
typedef struct node
{
struct node *left;
struct node *right;
char val;
}BTnode, *BTtree;
void CreateTree(BTtree &T)
{
char ch;
cin >> ch;
if(ch == '#') // Empty nodes are represented by 'ා' to end recursion
T = NULL;
else
{
T = new BTnode; //Apply for a new node space
T->val = ch;
CreateTree(T->left); //Recursively building left subtree
CreateTree(T->right); // Recursively building right subtree
}
}
void PreOrder(BTtree &T)
{
if(T)
{
cout<< T->val << ' ';
PreOrder(T->left);
PreOrder(T->right);
}
}
void InOrder(BTtree &T)
{
if(T)
{
InOrder(T->left);
cout<<T->val<<' ';
InOrder(T->right);
}
}
void PostOrder(BTtree &T)
{
if(T)
{
PostOrder(T->left);
PostOrder(T->right);
cout<<T->val<<' ';
}
}
//Non recursive first order traversal method in teaching materials
void PreOrderTraversal(BTtree &T)
{
stack<BTtree>st;
BTnode *p = T;
while(p!=NULL || !st.empty())
{
while(p!=NULL)
{
cout<<p->val<<' ';
st.push(p);
p = p->left;
}
if(!st.empty())
{
p = st.top();
st.pop();
p = p->right;
}
}
}
//Non recursive first order traversal method in teaching materials
void InOrderTraversal(BTtree &T)
{
stack<BTtree>st;
BTnode *p = T;
while(!st.empty() || p!=NULL)
{
while(p)
{
st.push(p);
p = p->left;
}
p = st.top();
cout<< p->val<<' ';
st.pop();
p = p->right;
}
}
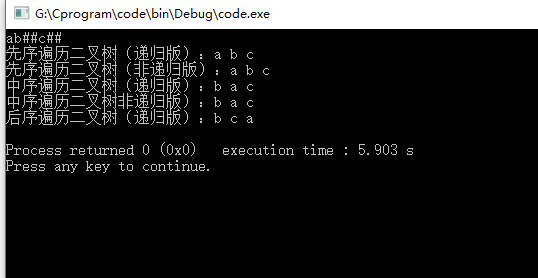
int main()
{
BTtree T;
CreateTree(T); //Building a binary tree
cout << "Traversing binary tree in sequence (recursive version):";
PreOrder(T);
cout<<endl;
cout << "Traversing binary tree in order (non recursive version):";
PreOrderTraversal(T);
cout<<endl;
cout << "Middle order traversal binary tree (recursive version):";
InOrder(T);
cout<<endl;
cout << "Middle order traversal binary tree non recursive version):";
InOrderTraversal(T);
cout<<endl;
cout << "Backward traversal of binary tree (recursive version):";
PostOrder(T);
cout<<endl;
return 0;
}