1445: Flat Painting

Time limit: 1000 ms memory limit: 65536 KB
Number of submissions: 565 passes: 296
[Title Description]
CE Digital has developed a product called Automatic Color Machine (APM).It can use predefined colors to color a flat panel of rectangles of different sizes that do not cover each other.

For coloring, the APM uses a set of brushes.Each brush is painted with a different color C.APM picks up a brush with colour C and colours all rectangles with colour C that meet the following restrictions:

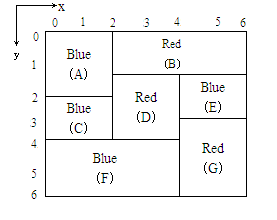
To avoid a color leak that mixes colors, a rectangle can only be colored after all rectangles immediately above it have been colored.For example, rectangle F in the diagram must be colored C and D before it can be colored.Note that each rectangle must be immediately coated, not just a portion.

Write a program to find a color scheme that minimizes the number of brushes that the APM picks up.Note that if a brush is picked up more than once, it must be counted in the total each time.

[Input]
Number N of first row rectangles.N lines below describe N rectangles.Each rectangle has five integer descriptions, the y and x coordinates in the upper left corner, the y and x coordinates in the lower right corner, and the preset color.

The color number is an integer from 1 to 20.

The upper left corner coordinates of the flat plate are always (0, 0).

The coordinate range is 0...99.N is less than 16.

[Output]
Minimum number of times to pick up the brush.

[Input Sample]
7
0 0 2 2 1
0 2 1 6 2
2 0 4 2 1
1 2 4 4 2
1 4 3 6 1
4 0 6 4 1
3 4 6 6 2
[Output Sample]
3

Idea: Optimize the read-in data, count the colors, and try each color once, that is, paint the colored and paintable bricks.Next painting cannot be applied with the last one.Finished recording results.
In order not to time out, two pruning prunes were added: Optimal pruning: Exit directly when the current number of colors is greater than or equal to the current answer.
Feasible pruning: If none of the bricks are currently painted, exit directly, and if you search again, there will be an additional number of times, and there may be an endless cycle.
As to whether the brick can be painted, pretreat it, record the bricks immediately above it in an array, and then judge if they have been painted.

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
inline int read()//Optimize read-in data
{
   int s=0,f=1;
   char ch=getchar();
   while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
   while(isdigit(ch)) s=s*10+ch-'0',ch=getchar();
   return s*f;
}
struct node  //Structure a1, b1 Brick upper left coordinate, a2, b2 lower right coordinate, x color
{
    int a1,b1,a2,b2,x;
}a[20];
int cmp(node a,node b)
{
    if(a.a1!=b.a1) return a.a1<b.a1;
    return a.b1<b.b1;
}
bool d=false;
int de[20];//The de array indicates whether or not the color is present
int n,m,ans=999,b[20],fk[20][20]; //b Array represents whether the brick has been painted
bool OK(int o)
{
    for(int i=1;i<=n;i++)
        if(fk[o][i]&&!b[i]) return false; //If i brick is next to o but i has not been painted, return false
    return true;
}
void dfs(int o,int pq,int xx)//o Number of colors pq colored bricks xx last colored
{
    if(o>=ans) return;//Exit directly if the current number of colors is greater than or equal to the current answer
    if(pq==n)//Finished, record answers
    {
        ans=o;
        return;
    }
    for(int i=1;i<=m;i++)//Enumerated colors
    {
        int oj=0;//Represents the number of bricks now painted in this color
        if(i!=xx&&de[i])//If there's this color, and it's not used last time
        {
            for(int j=1;j<=n;j++) //Painting
                if(!b[j]&&a[j].x==i&&OK(j))
				//If the brick has not been painted and can be painted
                    b[j]=1,oj++;
                else
				if(b[j]&&a[j].x==i)
				b[j]++;
           if(oj>0)
		   dfs(o+1,pq+oj,i);//If brick is applied, proceed to the next step
           for(int j=n;j>=1;j--)//To flash back
                if(b[j]==1&&a[j].x==i&&OK(j))
                    b[j]=0,oj--;
                else
				if(b[j]>1&&a[j].x==i)
				b[j]--; 
        }
    }
}
int main()
{
    n=read();
    for(int i=1;i<=n;i++)
        a[i].a1=read(),a[i].b1=read(),a[i].a2=read(),a[i].b2=read(),a[i].x=read(),
        a[i].a1++,a[i].b1++,de[a[i].x]++;//Record color
    for(int i=1;i<=20;i++)
	if(de[i])
	m=i; //Find Maximum Color Number
    sort(a+1,a+n+1,cmp);//Sort from smallest to largest by upper left coordinate size (vertical first, then horizontal)
    for(int i=2;i<=n;i++)
        for(int j=i-1;j>=1;j--)//fk[i][j] denotes whether the first brick is adjacent to the jth brick above
            if(a[i].a1==a[j].a2+1&&((a[i].b1>=a[j].b1&&a[i].b1<=a[j].b2)||(a[i].b2>=a[j].b1&&a[i].b2<=a[j].b2)))
                fk[i][j]=1;//If the top of the i-brick is next to the bottom of the j-brick and the horizontal coordinates of the two bricks overlap, that is, the j-brick is the i-brick next to the top of the brick
    dfs(0,0,0);
    printf("%d",ans);//Answer
    return 0;
}