In Java, floating-point types include float and double, which are mainly used to represent decimals. We often see that floating-point numbers have precision problems and are not suitable for comparing sizes or comparing equal logic. Any number in the computer is expressed in the binary form of 0 and 1, so how to use 0 and 1 for floating-point numbers?
Floating point binary calculation method
For the binary calculation of integers, use "divide by 2, take the remainder, and arrange in reverse order" to calculate the binary, as follows:
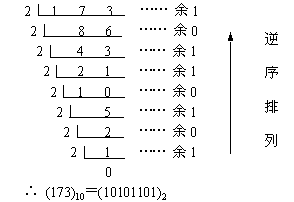
For binary calculation of decimals, use "multiply by 2, round and arrange in order" to calculate binary, as follows:

Floating point binary to decimal
To use binary to represent floating-point numbers is to make the decimal part can also be represented in binary. For the binary integer part, the lowest bit represents the 0th power of 2, which increases to the highest bit, which is the 1st power of 2, the 2nd power, the 3rd power... The highest bit of the decimal part is the - 1st power of 2, and the lowest bit is the - 2nd power of 2, the - 3rd power of 2... If the binary is 0, no calculation is performed, as shown in the following table.
| Binary | 1 | 1 | 1 | 1 | 1 | . | 1 | 1 | 1 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|
| 24 | 23 | 22 | 21 | 20 | decimal point | 2-1 | 2-2 | 2-3 | 2-4 | |
| decimal system | 16 | 8 | 4 | 2 | 1 | . | 1/2 | 1/4 | 1/8 | 1/16 |
Conversion example
| decimal system | Binary | Calculation method |
|---|---|---|
| 2.5 | 10.1 | 2.5=21+2-1 |
| 0.6 | 0.10011001... | 0.6=2-1+2-4+2-5+2-8+... |
Above, we found that 0.6 itself is not an infinite circular decimal, but it becomes an infinite circular decimal after it is expressed in binary. Computers cannot accurately store infinite cyclic binary numbers. They can only be rounded from 0 to 1.
Binary science and Technology Law
Binary science and technology method is to move the decimal point of binary to the left or right until the first place is 1, and then multiply it by the power of 2. Moving a few bits to the left is the power of 2, and moving a few bits to the right is the negative power of 2. The 0 or 1 after the decimal point is called the mantissa, and the power is called the exponent.
| decimal system | Binary | Binary science and Technology Law |
|---|---|---|
| 2.5 | 10.1 | 10.1=1.01 x 21 |
| 0.6 | 0.10011001... | 0.10011001...=1.0011001... x 2-1 |
To store a floating-point number in the computer, you also need a sign. Let's look at how floating point numbers are stored in a computer. In Java, floating point numbers include float and double, in which float accounts for 4 bytes [32 bits in total] and double accounts for 8 bytes [64 bits in total].
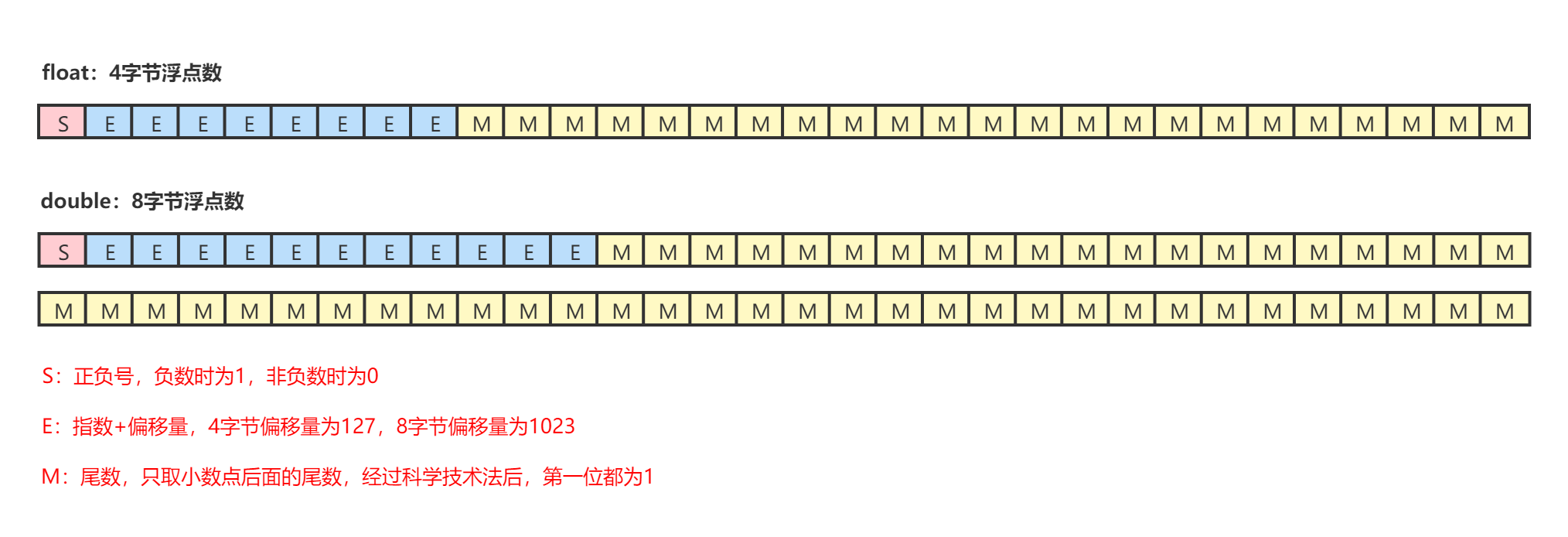
For float, the highest bit stores the sign, then the 8-bit stores the index, and the rest is used to store the mantissa. For the index part, the binary result after [index + offset] is actually stored. Because the index has a negative number, there will be no negative number after adding the offset.

case
After understanding the above floating point numbers, let's analyze why the classic [1-0.9] is not equal to 0.1.
First, let's learn how binary subtraction works, as follows:




To understand the operation method of binary subtraction, let's practice it through code:
- By calculating the binary result of float type 1-0.9, and then converting it to hexadecimal output result
- The steps of binary conversion to decimal are shown in the calculator below
/**
* @auther doaredo
* @mail doaredo@163.com
* @date 2021/07/31/1:22
* @description
*/
public class FloatDemo {
public static void main(String[] args) {
/*float Classic: 1-0.9*/
/*
Binary subtraction: 1-0.9
1.000000000000000000000000
-0.111001100110011001100110
=0.000110011001100110011010*/
float a = 1f;
float b = 0.9f;
// Results of direct Java computing
System.out.println(a - b);
// The result of binary subtraction
System.out.println(0.0625 +
0.03125 +
0.00390625 +
0.001953125 +
0.000244140625 +
0.0001220703125 +
0.0000152587890625 +
0.00000762939453125 +
9.5367431640625e-7 +
4.76837158203125e-7 +
1.1920928955078125e-7);
// We found that the result multiples calculated by ourselves are more than those calculated by Java
// Floating point numbers are automatically rounded in java
System.out.println(0.10000002384185791f);
}
}
Output results 0.100000024 0.10000002384185791 0.100000024
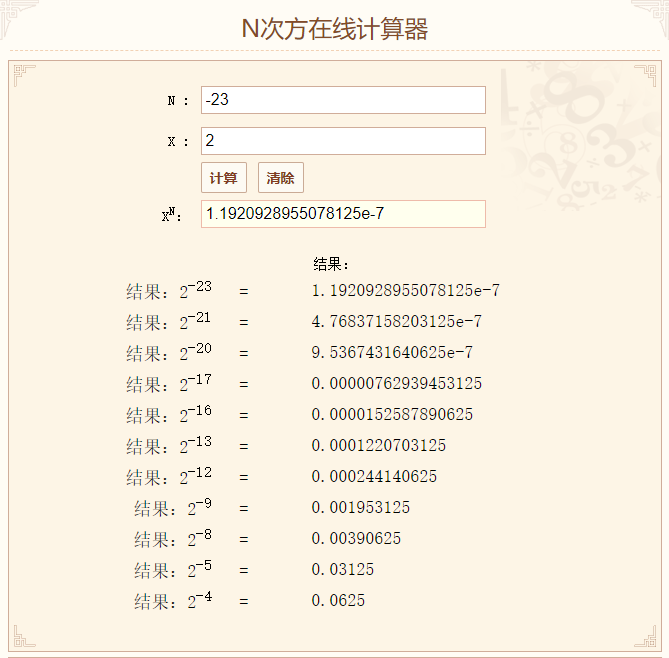
We specified the data type as float above. If it is not specified as float, it defaults to double.
- By calculating the binary result of double type 1-0.9, and then converting it to hexadecimal output result
- The steps of binary conversion to decimal are shown in the calculator below
/**
* @auther doaredo
* @mail doaredo@163.com
* @date 2021/07/31/1:22
* @description
*/
public class FloatDemo {
public static void main(String[] args) {
/*
* Classic: 1-0.9
* If it is not specified as float type, it defaults to double type floating-point number
* */
/*
Binary subtraction 1-0.9
1.00000000000000000000000000000000000000000000000000000
-0.11100110011001100110011001100110011001100110011001101
=0.00011001100110011001100110011001100110011001100110011*/
// java calculation results
System.out.println(1 - 0.9);
// The result of binary subtraction
System.out.println(0.0625
+ 0.03125
+ 0.00390625
+ 0.001953125
+ 0.000244140625
+ 0.0001220703125
+ 0.0000152587890625
+ 0.00000762939453125
+ 9.5367431640625e-7
+ 4.76837158203125e-7
+ 5.960464477539063e-8
+ 2.9802322387695312e-8
+ 3.725290298461914e-9
+ 1.862645149230957e-9
+ 2.3283064365386963e-10
+ 1.1641532182693481e-10
+ 1.4551915228366852e-11
+ 7.275957614183426e-12
+ 9.094947017729282e-13
+ 4.547473508864641e-13
+ 5.684341886080802e-14
+ 2.842170943040401e-14
+ 3.552713678800501e-15
+ 1.7763568394002505e-15
+ 2.220446049250313e-16
+ 1.1102230246251565e-16
);
}
}
Output results 0.09999999999999998 0.09999999999999998

floating-point comparisons
Due to the limited number of bit s occupied by floating-point numbers, when the integer part is too large, the decimal part is not fully used, resulting in accuracy problems.
/**
* @auther doaredo
* @mail doaredo@163.com
* @date 2021/07/31/1:22
* @description
*/
public class FloatDemo {
public static void main(String[] args) {
float c = 0.123456789f;
float d = 0.123456789f;
// The output is true
System.out.println(c==d);
float a = 12345678.009f;
float b = 12345678.000f;
// Because the integer digit occupies too many bit s, the decimal digit has no place and is ignored
// Because the decimal places are ignored, the actual comparison of the two numbers is equal
System.out.println(a==b);
}
}
Output results true true