Title Description

Difficult questions

Given two integers n and k, find out the number of different arrays that contain numbers from 1 to N and exactly have k reverse pairs.

The definition of reverse order pair is as follows: for the ith and jth elements of the array, if full I < j and a [i] > a [j], it is a reverse order pair; Otherwise not.

Since the answer may be large, you only need to return the value of the answer mod 10^9 + 7.

Sample

Example 1:

Input: n = 3, k = 0
Output: 1
Explanation:
Only the array [1,2,3] contains integers from 1 to 3 and has exactly 0 reverse pairs.
Example 2:

Input: n = 3, k = 1
Output: 2
Explanation:
Both arrays [1,3,2] and [2,1,3] have a pair in reverse order.

explain

The range of n is [1,1000] and the range of k is [0,1000].

thinking

Dynamic programming, using dp array of n+1 * k+1, dp[i][j] represents the number of arrays with length I and reverse order pair j
Initialization, dp[i][0] = 1, arbitrary length, reverse order pair is 0, that is, sequential row
The rest is 0
State transition, consider a slightly longer example, n = 5, k = 1;
Before adding 5, there are many kinds of arrangement of 4, which are not listed one by one. For example, consider 1 2 4 3, 1 2 3 4
When one reverse order pair is required, one is that there is an original reverse order pair, and then 5 is added to the last one, namely dp[4][1];
Or there is no reverse order pair. I use 5 to add an reverse order pair. 5 has_ 1_ 2_ 3_ 4_ Five positions can be inserted
Plug in 3_ Between 4, a reverse order pair will be constructed, and one more forward position will lead to one more reverse order pair, so it is also one, namely dp[4][0];

Therefore, dp[i][j] should be equal to the sum of all qualified dp[i-1][x],
The condition is that the original reverse order pair + insert the new reverse order pair can be equal to j,
At most, i-1 pairs can be added, (1_2_3_4 and 5 are inserted to the end, and 4 pairs in reverse order are added)
Therefore, if it does not exceed the boundary, dp[i][j] = dp[i-1][j-(i-1)] is added to dp[i-1][j];
When the boundary is exceeded, it is added from dp[i-1][0] to dp[i-1][j]
It is strongly recommended that you write with examples
In this way, the time complexity O(n^2 * k) will change TLE for each accumulation
Apply the official transfer formula

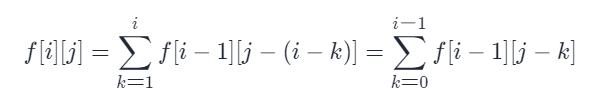
Optimized and observed
When it exceeds the boundary, dp[i][j] only adds one dp[i-1][j] more than dp[i][j-1];
Without exceeding the boundary, dp[i][j] is dp[i-1][j] more than dp[i][j-1] and dp[i-1][j-i] less
So you can add and subtract and optimize it to O(nk)
Continue to apply the official formula

In addition, when j is cycled, for example, n = 2 and K = 10, it does not need to be cycled so many times
When i is known, the maximum number of reverse order pairs is determined. When i is in reverse order, the reverse order pairs are the most
For example 4 3 2 1, where 43 42 41 32 31 21 is its reverse order pair, it is found that the law is the accumulation of 1 to 3
Generalization, for i, there are i-1 reverse order pairs; For i-1, there are i-2 reverse order pairs; For 1, there is no reverse order pair
Therefore, the maximum number of inverse pairs of length I is the accumulation of 1 to I-1, that is, (0+i-1)i/2. The sum of the first term plus the last term is divided by two
You can narrow down a portion of the loop

There is also mold taking, which is added in almost every place. It's really annoying

code

class Solution {
public:
    int kInversePairs(int n, int k) {
        if(n == 1 && k != 0) return 0;
        if(k == 0) return 1;
        int mod = 1000000007;
        vector<vector<int>> dp(n+1,vector<int>(k+1,0));
        for(int i = 1; i <= n; i++) {
            dp[i][0] = 1;
        }
        for(int i = 1; i <= n; i++) {
            int m = i*(i-1)/2;
            for(int j = 1; j <= m && j <= k; j++) {
                if(j < i) {
                    dp[i][j] = (dp[i][j-1]% mod + dp[i-1][j]%mod)% mod;
                }
                else dp[i][j] = (dp[i][j-1] + mod) % mod - (dp[i-1][j-i] + mod) % mod + (dp[i-1][j]+ mod) % mod;
                dp[i][j] = (dp[i][j]% mod + mod) % mod;
            }
        }
        return dp[n][k];
    }
};

result

Add an official explanation

class Solution {
private:
    static constexpr int mod = 1000000007;

public:
    int kInversePairs(int n, int k) {
        vector<vector<int>> f(2, vector<int>(k + 1));
        f[0][0] = 1;
        for (int i = 1; i <= n; ++i) {
            for (int j = 0; j <= k; ++j) {
                int cur = i & 1, prev = cur ^ 1;
                f[cur][j] = (j - 1 >= 0 ? f[cur][j - 1] : 0) - (j - i >= 0 ? f[prev][j - i] : 0) + f[prev][j];
                if (f[cur][j] >= mod) {
                    f[cur][j] -= mod;
                }
                else if (f[cur][j] < 0) {
                    f[cur][j] += mod;
                }
            }
        }
        return f[n & 1][k];
    }
};

The official space is also optimized. After all, only the previous value is used

summary

For dynamic programming, we mainly use handwritten examples to understand, and then find laws and optimization