subject

Given an array of candidates without duplicate elements and a target number target, find all combinations in candidates that can make the sum of numbers target.

The number in candidates can be selected repeatedly without limit.

explain:

All numbers (including target) are positive integers.
The solution set cannot contain duplicate combinations.

Train of thought backtracking algorithm

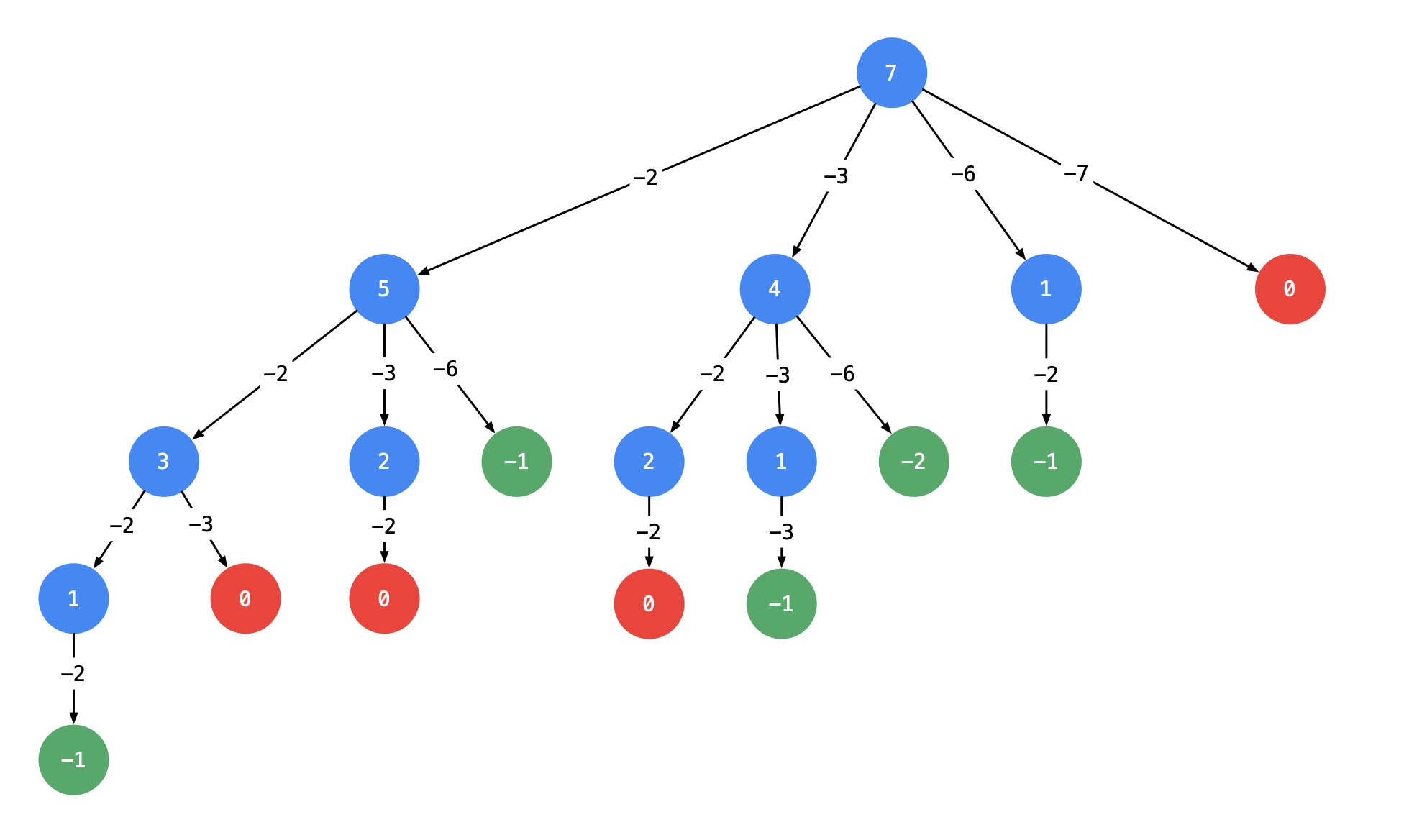
Take the input: candidates = [2, 3, 6, 7], target = 7 as an example:

explain:

Take target = 7 as the root node and subtract when creating a branch;
Each arrow indicates that the value of the child node is obtained by subtracting the value on the edge from the value of the parent node. The value of the edge is the value of each element of the candidate array given in the title;
Stop when it is reduced to 00 or negative, that is, node 00 and negative nodes become leaf nodes;
All paths from root node to node 00 (only from top to bottom, no loop) are the result of the problem.
This tree has 44 leaf nodes with the value of 00, and the corresponding path list is [[2, 2, 3], [2, 3, 2], [3, 2, 2], [7]], while the output given in the example is only [[7], [2, 2, 3]]. That is: the problem requires that each qualified solution is not calculated in order. Let's analyze why duplication occurs.

Analyze the causes (difficulties) of repeated paths according to specific examples
Friendly tip: my description of this part is obscure. I suggest you first observe the causes of repetition and then think about how to solve it.

The reason for duplication is that when subtracting and expanding branches at each node, because the title says that each element can be reused, we consider all the candidates, so there is a duplicate list.

A simple de duplication scheme is based on the natural de duplication function of hash table, but it is not so easy to operate.

Can I redo it when searching? The answer is yes. When we encounter the problem that the same elements do not calculate the order, we need to search in a certain order when searching. The specific method is to set the starting point begin of the next round of search every time. Please see the figure below.

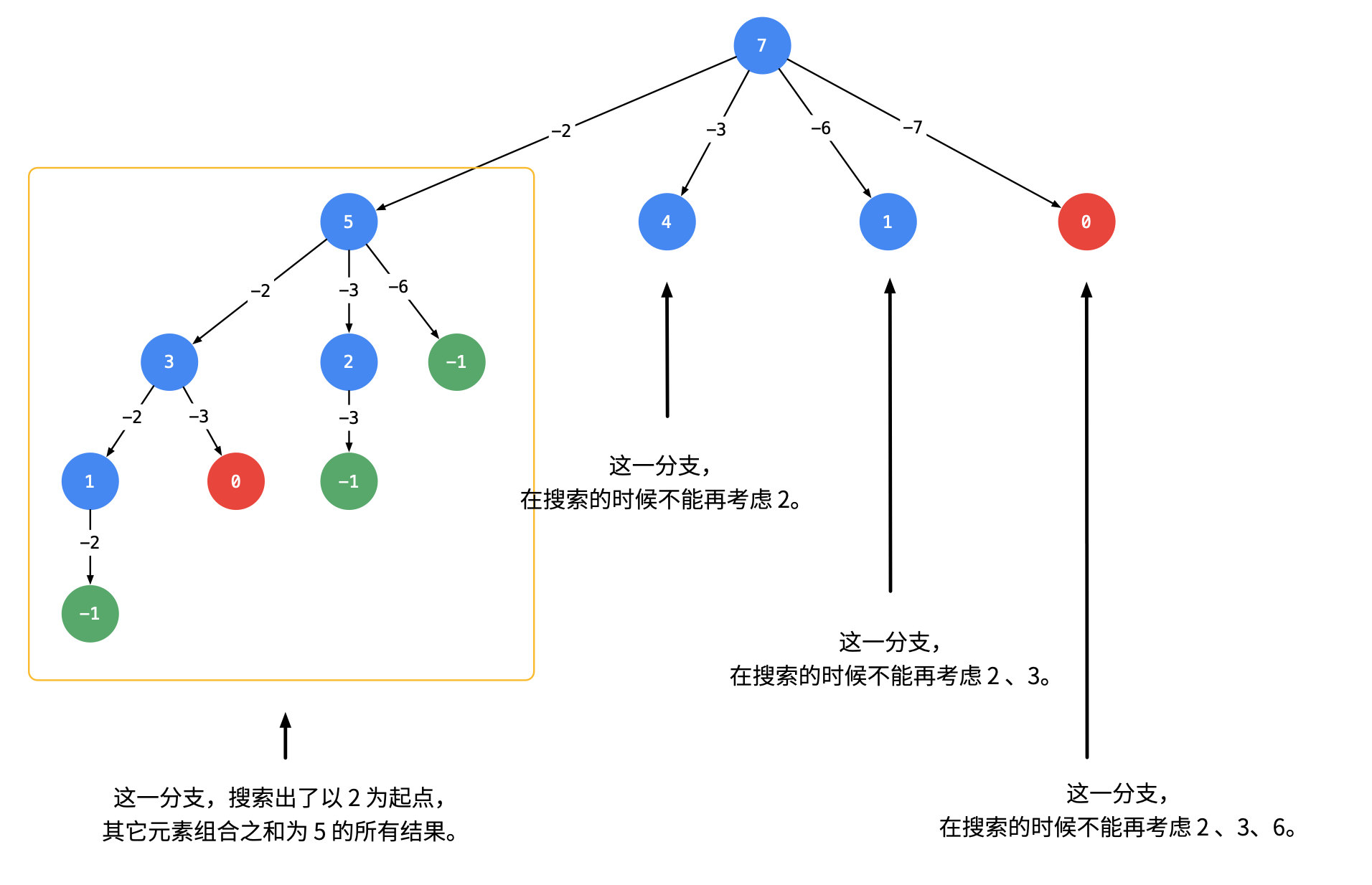
That is, starting from the 22nd node of each layer, you can no longer search the elements in the candidate used by the nodes of the same layer.

The [1,2] + [3] syntax of Python 3 generates a new list. After it is transferred to the root node layer by layer, it can be directly res.append(path);
Since there is no change in the parameter type of Python 3, it seems that there is no change in the parameter type in the code.

from typing import List


class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:

        def dfs(candidates, begin, size, path, res, target):
            if target < 0: # non-existent
                return
            if target == 0:
                res.append(path) # Update path
                return

            for index in range(begin, size):# The index position should be between the starting parameter and the array length
                dfs(candidates, index, size, path + [candidates[index]], res, target - candidates[index]) # Update dfs and begin to the new index. Add the value of the previous index to the path and subtract the new index from the target. For example, if the last subtraction is 0, it means that this array is true. Take this as a cycle

        size = len(candidates) #Determine that size is the length of the array
        if size == 0:
            return []
        path = []
        res = []
        dfs(candidates, 0, size, path, res, target)
        return res

Another way of thinking

Variable meaning: use indicates the number (list) that has been used, and remain indicates the distance from target.

Sort candidates in ascending order so that you can use return to reduce the search space according to the size of remain;
Recursively find possible combinations. Specifically, each recursion will traverse all candidates. The case is 3:1. If the conditions are met, add one answer; 2. If it is insufficient, continue recursion; 3. If it exceeds, directly exit the route.
Note that each layer of recursion traverses all candidates, which will lead to symmetrical repeated answers such as [2,2,3], [3,2,2]. This is because of the "forward selection" situation. Each deeper recursion reduces one candidate backward, and the forced function can only "select backward", which will not produce repeated answers.

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        candidates = sorted(candidates) #Sort the array first

        ans = []

        def find(s, use, remain):
            for i in range(s, len(candidates)): # Defines that the loop range is between the beginning and the length of the array
                c = candidates[i] # c is the value in the array
                if c == remain: # Suppose the value of c is equal to the residual value after subtraction
                    ans.append(use + [c]) #The combination has been found
                if c < remain: #If C is less than the residual value, it can be reduced. So we need to update the current scope. The initial value changes from s to i, use to use+c, and the remaining value changes to remain-c
                    find(i, use + [c], remain - c)
                if c > remain: #c is greater than the residual value and cannot be reduced. Give up
                    return
        find(0, [], target) # Start at 0. The initial value of the residual value is target. Put the use d value into []

        return ans