Yang Hui triangle

• Topic introduction
  

• Train of thought analysis

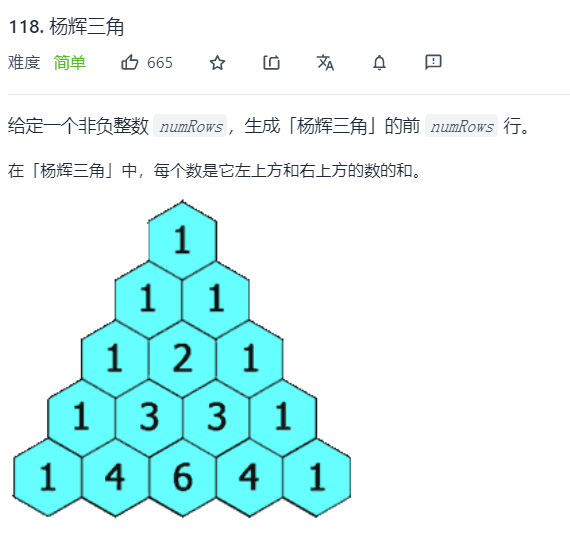
  1. First of all, we need to understand how the Yang Hui triangle was formed. As shown in the figure, the beginning and end numbers of each layer are 1, and the number of each remaining position is equal to the sum of the number of the corresponding position of its upper layer and the number of the previous position.
  2. So we can use one List to store the data of each layer, and then use another List to store each layer.

• Related code snippets

class Solution {
    public List<List<Integer>> generate(int numRows) {
        List<List<Integer>> list = new ArrayList<List<Integer>>();
        for (int i = 0; i < numRows; ++i) {
            List<Integer> list1 = new ArrayList<Integer>();
            for (int j = 0; j <= i; ++j) {
                if (j == 0 || j == i) {
                    list1.add(1);
                } else {
                    list1.add(list.get(i - 1).get(j - 1) + list.get(i - 1).get(j));
                }
            }
            list.add(list1);
        }
        return list;
    }
}

Yanghui triangle II

• Topic introduction
  
  

• Train of thought analysis

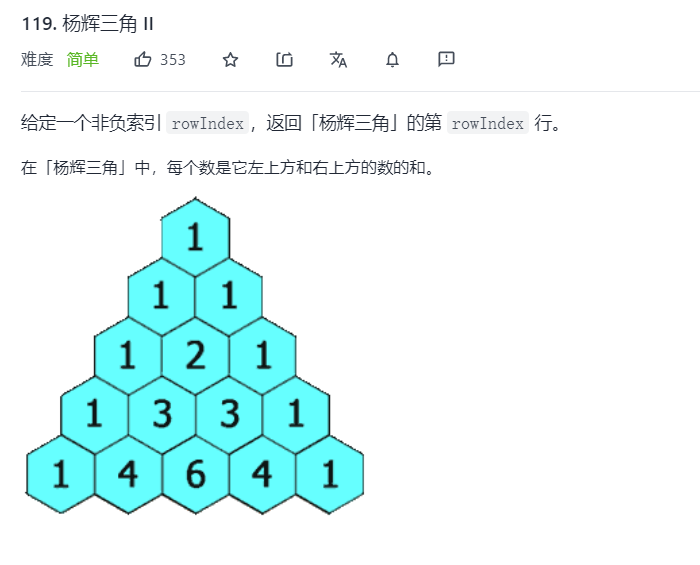
  1. This question is very similar to the first question. The only difference is that it seeks the data of a specific layer of Yang Hui triangle, and the number of layers is recorded from 0.
  2. However, according to the requirements in the advanced, we can't store all the data of all the rows before a row of Yang Hui triangle like the first question. According to the nature of Yang Hui triangle, we can get that the data start of a row of Yang Hui triangle directly depends on the data of the previous row. Therefore, we can use a List to store only the data of the previous row.

• Related code snippets

class Solution {
    public List<Integer> getRow(int rowIndex) {
       List<Integer> list  = new ArrayList<>();
       for(int i = 0; i <= rowIndex; i++){
           List<Integer> list1 = new ArrayList<>();
           for(int j = 0; j <= i; j++){
               if(j == 0 || j == i){
                   list1.add(1);
               }else{
                   list1.add(list.get(j)+list.get(j-1));
               }
           }
           list = list1;
       }
       return list;
    }
}

Picture smoother

• Topic introduction
  

• Train of thought analysis

  1. According to the title, we know that it is to find the average value of the Jiugong lattice centered on each number in the two-dimensional array, which is a bit similar to "minesweeping".
  2. The disgusting part of this problem lies in the treatment of the boundary, because the number of significant digits in the boundary changes with the scale of the matrix. Therefore, in order to facilitate the treatment of the boundary of the matrix, we can add a new boundary to the existing matrix, that is, A[m][n] is stored in B[m+2][n+2].
  3. Then we separately consider the influence of matrix scale on the significant number of boundary. For the elements of the four vertices of the matrix, when the scale of the matrix is 1x1, the number of significant digits is 1; When the scale is 1xk or kx1, the number of significant digits is 2; The effective number of remaining scales is 4. For the elements whose vertices are removed from the four boundaries of the matrix, when the scale of the matrix is 1xk or kx1, the number of significant digits is 4; The effective number of other scales is 6 (regardless of only 1 element). The effective number of remaining elements is 9.

• Related code snippets

class Solution {
    public int[][] imageSmoother(int[][] img) {
        int row = img.length;
        int col = img[0].length;
        int[][] sum = new int[row][col];
        int[][] newImg = new int[row+2][col+2];
        for(int i = 1; i < row+1;i++){
            for(int j = 1; j < col + 1; j++){
                newImg[i][j] = img[i-1][j-1];
            }
        }
        for(int i = 1; i < row + 1; i++){
            for(int j = 1; j < col + 1; j++){
                sum[i-1][j-1] = (newImg[i-1][j-1]+newImg[i-1][j]+newImg[i-1][j+1]+
                        newImg[i][j-1]+newImg[i][j]+newImg[i][j+1]+
                        newImg[i+1][j-1]+newImg[i+1][j]+newImg[i+1][j+1]);
                int k = 0;
                if(i==1&&j==1||(i==1&&j==col)||(i==row&&j==1)||(i==row&&j==col)){
                    if(row == 1 && col == 1){
                        k = 1;
                    }else if(row == 1||col == 1){
                        k = 2;
                    }else{
                        k = 4;
                    }
                }else if(i==1||i==row||j==1||j==col){
                    if(row == 1|| col == 1){
                        k = 3;
                    }else{
                        k = 6;
                    }
                }else{
                    k = 9;
                }
                sum[i-1][j-1] /= k;
            }
        }
        return sum;
    }
}

Range summation

• Topic introduction
  
  

• Train of thought analysis

  1. Firstly, the notice of the topic has given a hint: the maximum m and n can reach 40000. For a two-dimensional array, it can not be opened to such a large size under normal circumstances. So consider other "efficient" methods.
  2. We can see from the first example: in the two operations, the second operation covers the first one, so the first operation covers the maximum number of elements. According to this, we can think that the essence of this problem is to find the minimum value of the abscissa and the minimum value of the ordinate of all operations, and then multiply them. Of course, it should be noted that when the number of operations is 0, the maximum number of elements is all the original data.

• Related code snippets

class Solution {
    public int maxCount(int m, int n, int[][] ops) {
      int res = m * n;
        if(ops.length == 0){
            return res;
        }
        int rmin = ops[0][0];
        int cmin = ops[0][1];
        for(int i = 0; i < ops.length;i++){
            if(rmin > ops[i][0]){
                rmin = ops[i][0];
            }
            if(cmin > ops[i][1]){
                cmin = ops[i][1];
            }
        }
        return rmin * cmin;
    }
}

summary

The topic of this summary is mainly about two-dimensional array and rolling array. When solving the problem of two-dimensional array, our priority is to estimate the scale of two-dimensional array and give priority to the boundary of two-dimensional array and some special conditions; Rolling array essentially embodies the idea of recursion. According to the previous recursion, the following are connected layer by layer. Of course, the topic itself is still very simple, ha ha, Wu Wu.. I hope you can gain something!