subject
Here are the head nodes headA and headB of the two single linked lists. Please find and return the starting node where the two single linked lists intersect. If there is no intersecting node between the two linked lists, null is returned.
As shown in the figure, two linked lists intersect at node c1:
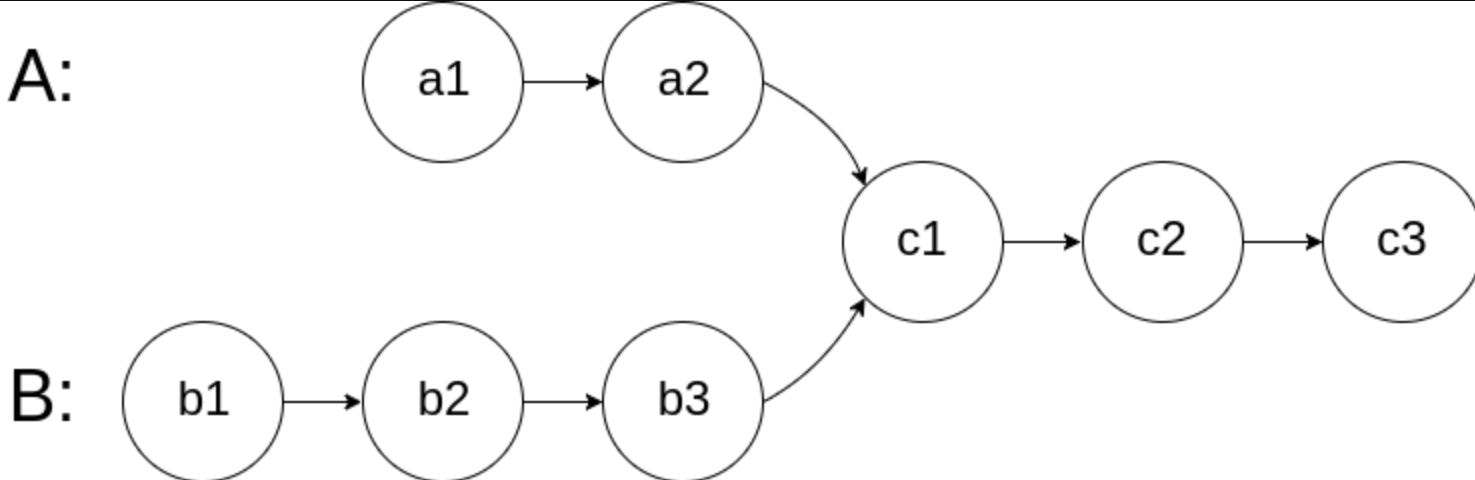
The title data ensures that there are no links in the whole chain structure.
Note that after the function returns the result, the linked list must maintain its original structure.
Custom profiling:
The input of the evaluation system is as follows (the program you designed does not apply to this input):
intersectVal - the value of the starting node of the intersection. If there are no intersecting nodes, this value is 0
listA - the first linked list
listB - second linked list
Skippa - the number of nodes that jump to the cross node in listA (starting from the head node)
skipB - the number of nodes that jump to the cross node in listB (starting from the head node)
The evaluation system will create a linked data structure based on these inputs and pass the two head nodes headA and headB to your program. If the program can correctly return the intersection node, your solution will be regarded as the correct answer.
Example 1:
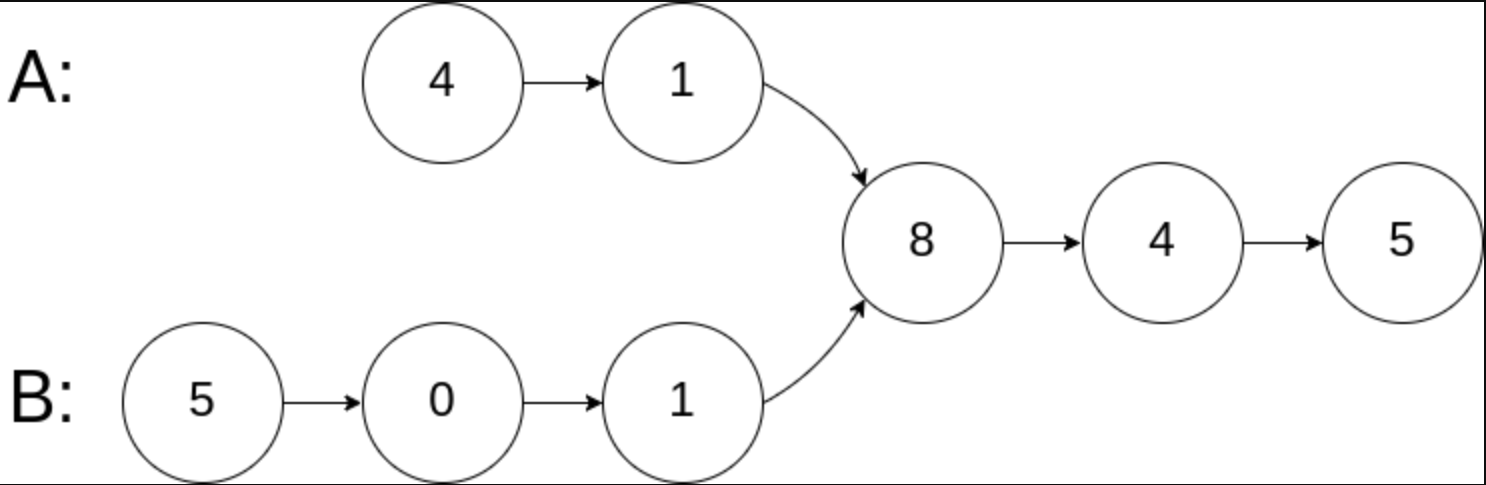
Input: intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
Output: Intersected at '8'
Explanation: the value of intersection node is 8 (note that if two linked lists intersect, it cannot be 0).
Starting from the respective header, linked list A is [4,1,8,4,5], and linked list B is [5,6,1,8,4,5].
In A, there are 2 nodes before the intersection node; In B, there are three nodes before the intersection node.
Example 2:
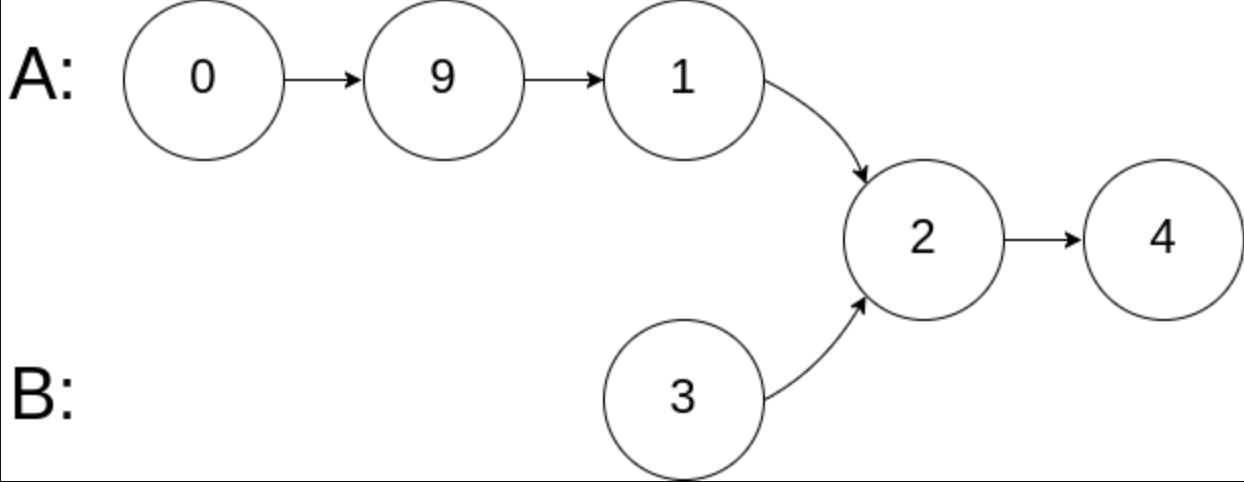
Input: intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
Output: Intersected at '2'
Explanation: the value of intersection node is 2 (note that if two linked lists intersect, it cannot be 0).
Starting from the respective header, linked list A is [1,9,1,2,4], and linked list B is [3,2,4].
In A, there are 3 nodes before the intersection node; In B, there is one node before the intersection node.
Example 3:
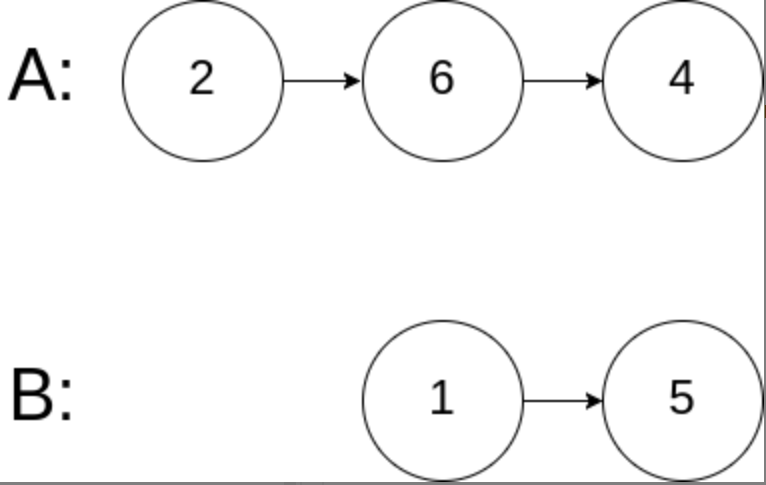
Input: intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
Output: null
Explanation: starting from the respective header, linked list A is [2,6,4], and linked list B is [1,5].
Because the two linked lists do not intersect, intersectVal must be 0, and skipA and skipB can be any value.
The two linked lists do not intersect, so null is returned.
Tips:
The number of nodes in listA is m
The number of nodes in listB is n
1 <= m, n <= 3 * 104
1 <= Node.val <= 105
0 <= skipA <= m
0 <= skipB <= n
If listA and listB have no intersection, intersectVal is 0
If listA and listB have an intersection, intersectVal == listA[skipA] == listB[skipB]
Advanced: can you design a solution with time complexity O(m + n) and only O(1) memory?
Source: LeetCode
Link: https://leetcode-cn.com/problems/intersection-of-two-linked-lists
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.
Solution 1: hash set
One hash table is stored, and then the other is used to judge.
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
Set <ListNode> visited= new HashSet<ListNode>();
ListNode temp=headA;
while(temp!=null){
visited.add(temp);
temp=temp.next;
}
temp=headB;
while(temp!=null){
if(visited.contains(temp)){
return temp;
}
temp=temp.next;
}
return null;
}
}
Time complexity: O(m+n)O(m+n), where mm and nn are the lengths of linked lists \ textit{headA}headA and \ textit{headB}headB, respectively. You need to traverse the two linked lists once each.
Spatial complexity: O(m)O(m), where mm is the length of the linked list \ textit{headA}headA. You need to use a hash set to store all nodes in the linked list \ textit{headA}headA.
Solution 2: double pointer
The double hands start from the beginning and then change the order. We met. That is, 2 + 3 = 3 + 2
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if(headA==null || headB==null){
return null;
}
ListNode pA=headA,pB=headB;
while(pA!=pB){
pA=(pA==null)? headB:pA.next;//headB easy Ctrip pB
pB=(pB==null)? headA:pB.next;
}
return pB;
}
}
Time complexity: O(m+n)O(m+n), where mm and nn are the lengths of the linked list headA and headB respectively. Two pointers traverse two linked lists at the same time, and each pointer traverses two linked lists once each.
Space complexity: O(1).
Solution 3: the length difference of the elderly is transformed, and then the two enter one at the same time
Calculate the length of the two and get the length difference. The elder enters the length of the length difference, and then the two enter one at the same time
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
int L1=0,L2=0,dif=0;
ListNode h1=headA,h2=headB;
while(h1!=null){
L1++;
h1=h1.next;
}
while(h2!=null){
L2++;
h2=h2.next;
}
if(L1<L2){
h1=headB;
h2=headA;
dif=L2-L1;
}
else{
h1=headA;
h2=headB;
dif=L1-L2;
}
for(int i=0;i<dif;i++){
h1=h1.next;
}
while(h1!=null&&h2!=null){
if(h1==h2){
return h2;
}
h1=h1.next;
h2=h2.next;
}
return null;
}
}