Fractal tree detailed tutorial
1, Introduction
Fractal is the geometry of nature---- - Mandelbrot (founder of fractal theory)
Through this study, I learned how to make a fractal tree and was deeply attracted by him. Finally, I can make some suggestions as follows:
Falling phoenix tree, falling Bauhinia tree, cherry petal falling tree and falling Jacaranda tree

task
2.2 draw fractal tree or other fractal graphics with reference to the concept of fractal. It is required that you can save and open the drawing.
http://www.matrix67.com/blog/archives/6231
https://www.zhihu.com/question/271643290/answer/525019532
2, Experimental environment
Visual stdio 2017
Windows Forms application
3, Experimental process
thinking
1. The concept of fractal and the establishment of fractal theory
2. Create a form
3. Generate fractal tree
4. Realize file saving and opening and Bitmap class
5. Display of fractal tree and other fractal graphics derived from it
1. The concept of fractal and the establishment of fractal theory
Fractal is fractal in English, It was created by the American French mathematician Benoit Mandelbrot. This word comes from the Latin adjective fractus, and the corresponding Latin verb is fragment. In addition, this word is similar to the English fraction and fragment (fragment) has the same root. Before the mid-1970s, Mandelbrot had always used the English word fractal to express his fractal thought. Therefore, the fractal synthesized by taking the head of the Latin word and the tail of the English word originally meant irregular, broken and fractional. Mandelbrot wanted to use this word to describe what traditional Euclidean geometry in nature could not describe A large class of complex irregular geometric objects. For example, winding coastlines, fluctuating mountains, rough sections, changeable clouds, winding rivers, crisscross blood, dazzling stars, etc. Their common feature is extremely irregular or extremely unsmooth. Intuitively and roughly, these objects are fractal.
In 1975, Mandelbrot published his French monograph Les objects fractals: form, opportunity and dimension, marking the official birth of fractal theory. In 1977, he published the English translation of the book. In 1982, Mandelbrot published another historical book, fractal geometry of nature Meet with readers. Although the book is a supplement to the previous book, it is a "Manifesto" of fractal theory in Mandelbrot's view, and in the eyes of fractal fans, it is undoubtedly a "Bible". The book is full of quotations, pictures and texts. It examines many phenomena in nature from the perspective of fractal, which has attracted extensive attention in the academic circles, and Mandelbrot became famous at one stroke. since then, the continuous fractal heat has attracted the attention of many scientists and scholars all over the world. Their research work in their respective fields has made fractal theory blossom everywhere.
2. Create a form
Create a canvas, some controls and buttons, drop-down menus, scroll bars, and so on
The final results are shown in the figure:
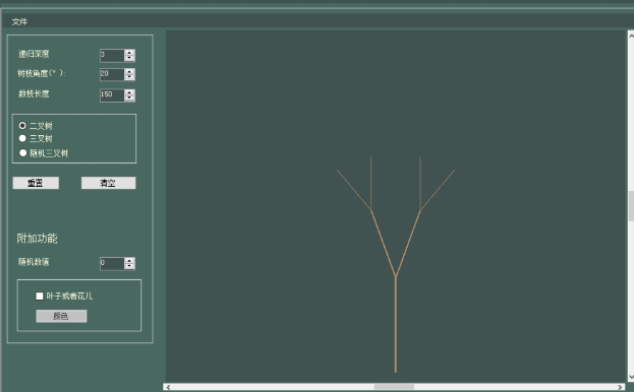
In order to make the interface more beautiful, I use a color card, take the color with PS, and extract the dark green as the background and light orange as the trunk
Dark green as background
this.picBoxCanvas.BackColor = Color.FromArgb(64, 83, 81);//Dark green background color
Light orange as trunk
treeTrunkPen = new Pen(Color.FromArgb(181, 143, 107));//New trunk brush
3. Generate fractal tree
Draw a picture DrawScene()function: Because of the line drawing function graphics.DrawLine()Can only accept float type therefore y0 ,height, width ,xloc0 Equal variables are used float type
Initialize the tree so that the newly generated tree is located in the center of the screen
float xloc0 = width / 2.0f; float yloc0 = (y0 + height) - YOffset;
Initialization tree position display:
Draw the complete code of the picture:
private void DrawScene()
{
float y0 = 0.0f;
float height = this.picBoxCanvas.Height;//Is the height of the canvas
float width = this.picBoxCanvas.Width;Is the width of the canvas
//Make the initialized tree in the middle
float xloc0 = width / 2.0f;
float yloc0 = (y0 + height) - YOffset;
float xloc1 = xloc0;
float yloc1 = yloc0 - Length;
//Draw branches
DrawBranch(settings.Depth, xloc0, yloc0, settings.Length, initBranchAngle, scaledLength, settings.Angle);
}
Draw branches
The next step is to realize the function of drawing branches:
Definition of each variable:
/// <summary> ///Draw branches /// </summary> ///< param name = "depth" > recursion depth < / param > ///< param name = "X" > x indicates the starting point of the branch < / param > ///< param name = "Y" > y indicates the starting point of the branch < / param > ///< param name = "length" > indicates the length of the branch < / param > ///< param name = "theta" > indicates the angle of the branch < / param > ///< param name = "scaledlength" > calculate the number of consecutive branches proportionally < / param > ///< param name = "delta theta" > angle change of continuous branches < / param >
The apex of a branch
So when things change
// x1, y1 calculate the end of branch connection
// sin is equal to the opposite side than the hypotenuse, cos is equal to the adjacent side than the hypotenuse (the length is equal to the hypotenuse)
x1 = X + length * (float)Math.Cos(theta * RadiansPerDegree); // Increase x (make it change from left to right)
y1 = Y - length * (float)Math.Sin(theta * RadiansPerDegree); // Reduce y (let it change from bottom to top)
//For example, y's minus becomes + and it will grow backwards
Width / thickness of trunk
Defines the width of the trunk
treeTrunkPen.Width = treeTrunkWidths[depth];
The array here uses the above customized array
The increasing number makes the final trunk have different thickness to better simulate the growth of the tree
//Trunk thickness
private int[] treeTrunkWidths = { 0, 1, 2, 3, 4, 6, 9, 11, 14, 17 };
Because the Trident tree is very large and messy, the tree width of a very long array is not set
Draw a line: draw a line between X, y, X1 and Y1. This function can only accept float type
graphics.DrawLine(treeTrunkPen, X, Y, x1, y1);//Draw a line between X, Y, x1, y1
Recursive tree growth
Trees in nature also have fractal structure. A trunk grows two side trunks, and each side trunk grows two side trunks. By analogy, it grows a dense structure. This growth structure can also be simulated by fractal recursive algorithm, but it is not as natural as trees in nature. (therefore, in this experiment, I try to add random values to make the tree more natural and ecological)
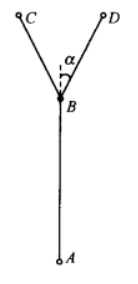
- Recursive fractal tree 1 (1) as shown in the figure above is the generator of the bifurcation tree. The process of generating the bifurcation tree by using the recursive algorithm is actually the process of constantly redrawing the generator at each level. The specific steps are as follows:
① set up A The point coordinates are( x,y),B The point coordinates are( xo,y0),C The point coordinates are( x1,y1),D The point coordinates are( x2,y2),L Is the length of the trunk,αIs the angle between the branch and the trunk. ② Draw trunk AB,Namely( x,y)-(xo,yo)Straight line. ③ calculation C Point coordinates, L=scaledLength×L,x=x+L×cosα,y=y0-L×sina. ④ calculation D Point coordinates, L=scaledLength×L,x1=xo+L×cos(-α),y1=y0-L×sin(-α). ⑤ Will step②in x→x,y0→y,x1→x0,y1→y0,Redrawn( x,y)-(x0,y0)Straight line, that is, draw branches BC. ⑥ Will step②in x→x,y0→y,x2→x0,y2→y0,Redrawn( x,y)-(xo,y0)Straight line, that is, draw branches BD. ⑦Repeat step③~step⑥,Number of recursions until completion.
Note: during initialization, I adjust scaledLength to three quarters
private const float scaledLength = 0.75f;
In addition, in this example, by making depth - so that the trunk becomes thinner in the process of drawing fractal tree, the effect of tree is formed
At the same time, it also realizes the generation of trigeminal tree. The following is a comparison between the two:
1. Binary tree generation process:
Recursive call ----- > draw the angle change of right + continuous branches
Recursive call ----- > draw the angle change of left + continuous branches
2. Trigeminal tree generation process:
Recursive call ----- > draw the angle change of right + continuous branches
Recursive call ----- > middle edge drawing (without changing the angle)
Recursive call ----- > draw the angle change of left + continuous branches
// If it is not the top branch, draw the connected branch
if (depth > 1)
{
//A trigeminal tree has only one more middle branch than a binary tree
// Recursive call - draw right + delta theta (binary + trigeminal)
DrawBranch(depth - 1, x1, y1, (length * scaledLength) + randomnessRightHandSide, (theta + deltaTheta) + randomnessRightHandSide, scaledLength, deltaTheta);
if (settings.RandomThirdBranch)//Random trigeminal tree
{
int drawMiddleBranch = randomMiddleBranch.Next(0, 2);
if (drawMiddleBranch == 0)
{
// Draw middle
DrawBranch(depth - 1, x1, y1, (length * scaledLength) + randomnessLeftHandSide, theta + randomnessLeftHandSide, scaledLength, deltaTheta);// randomnessRightHandSide random value
}
}
else if (settings.ThreeBranches)//Trident tree
{
// Draw middle
DrawBranch(depth - 1, x1, y1, (length * scaledLength) + randomnessLeftHandSide, theta + randomnessLeftHandSide, scaledLength, deltaTheta);
}
// Recursive call - draw left - Delta theta (binary + trigeminal)
DrawBranch(depth - 1, x1, y1, (length * scaledLength) + randomnessLeftHandSide, (theta - deltaTheta) + randomnessLeftHandSide, scaledLength, deltaTheta);
}
// If it's a vertex leaf
else if (depth == 1)
{
if (settings.EndLeaves)//You can draw leaves or pictures
{
// So far, the end leaf is just a circle (bitmap can also be used)
graphics.DrawArc(endLeavesPen, x1 - 2, y1 - 2, 6, 6, 0, 360);
graphics.DrawArc(endLeavesPen, x1 - 2, y1 - 2, 4, 4, 0, 360);
}
}
}
Draw leaves or flowers
Click on the panel of the form application below

else if (depth == 1)//If you reach the leaves
{
if (settings.EndLeaves)//You can draw leaves or pictures
{
// So far, the end leaf is just a circle (bitmap can also be used)
graphics.DrawArc(endLeavesPen, x1 - 2, y1 - 2, 6, 6, 0, 360);//circle
graphics.DrawArc(endLeavesPen, x1 - 2, y1 - 2, 4, 4, 0, 360);
}
}
Exhibition:

We naturally think about how to add more leaves or petals (even snow on trees)
So this code can be improved
graphics.DrawArc(endLeavesPen, x1 - 2, y1 - 2, 6, 10, 0, 180); graphics.DrawArc(endLeavesPen, x1 - 4, y1 - 4, 3, 4, 0, 180); graphics.DrawArc(endLeavesPen, x1 - 3, y1 - 3, 6, 10, 0, 180); graphics.DrawArc(endLeavesPen, x1 - 2, y1 - 2, 3, 4, 0, 180); graphics.DrawArc(endLeavesPen, x1 - 6, y1 - 7, 6, 10, 0, 180); graphics.DrawArc(endLeavesPen, x1 - 2, y1 - 3, 3, 4, 0, 180);

Realize random
if (settings.RandomThirdBranch)//Random trigeminal tree
{
int drawMiddleBranch = randomMiddleBranch.Next(0, 2);//Here complete the random branch number
if (drawMiddleBranch == 0)
{
// Draw middle
DrawBranch(depth - 1, x1, y1, (length * scaledLength) + randomnessLeftHandSide, theta + randomnessLeftHandSide, scaledLength, deltaTheta);// randomnessRightHandSide implements random values
}
}

Function code:
private void DrawBranch(int depth, float X, float Y, float length, float theta, float scaledLength, float deltaTheta)
{
float x1;
float y1;
// x1, y1 calculate the end of branch connection
// sin is equal to the opposite side than the hypotenuse, cos is equal to the adjacent side than the hypotenuse (the length is equal to the hypotenuse)
x1 = X + length * (float)Math.Cos(theta * RadiansPerDegree); // Increase x (make it change from left to right)
y1 = Y - length * (float)Math.Sin(theta * RadiansPerDegree); // Reduce y (let it change from bottom to top)
//For example, y's minus becomes + and it will grow backwards
treeTrunkPen.Width = treeTrunkWidths[depth];
graphics.DrawLine(treeTrunkPen, X, Y, x1, y1);//Draw a line between X, Y, x1, y1
// If it is not the top branch, draw the connected branch
if (depth > 1)
{
//A trigeminal tree has only one more middle branch than a binary tree
// Recursive call - draw right + delta theta (binary + trigeminal)
DrawBranch(depth - 1, x1, y1, (length * scaledLength) + randomnessRightHandSide, (theta + deltaTheta) + randomnessRightHandSide, scaledLength, deltaTheta);// randomnessRightHandSide random value
if (settings.RandomThirdBranch)//Random trigeminal tree
{
int drawMiddleBranch = randomMiddleBranch.Next(0, 2);
if (drawMiddleBranch == 0)
{
// Draw middle
DrawBranch(depth - 1, x1, y1, (length * scaledLength) + randomnessLeftHandSide, theta + randomnessLeftHandSide, scaledLength, deltaTheta);
}
}
else if (settings.ThreeBranches)//Trident tree
{
// Draw middle
DrawBranch(depth - 1, x1, y1, (length * scaledLength) + randomnessLeftHandSide, theta + randomnessLeftHandSide, scaledLength, deltaTheta);
}
// Recursive call - draw left - Delta theta (binary + trigeminal)
DrawBranch(depth - 1, x1, y1, (length * scaledLength) + randomnessLeftHandSide, (theta - deltaTheta) + randomnessLeftHandSide, scaledLength, deltaTheta);
}
// If it's a vertex leaf
else if (depth == 1)
{
if (settings.EndLeaves)//You can draw leaves or pictures
{
// So far, the end leaf is just a circle (bitmap can also be used)
graphics.DrawArc(endLeavesPen, x1 - 2, y1 - 2, 6, 6, 0, 360);
graphics.DrawArc(endLeavesPen, x1 - 2, y1 - 2, 4, 4, 0, 360);
}
}
}
4. Realize file saving and opening and Bitmap class
Bitmap class
Bitmap Class is Image Class, which can load and display various bitmap images. The image consists of a series of If you know the information of each pixel, you know the whole image. A bitmap image is created by storing all pixels Information to describe the image. GDI+Supports a variety of image file formats, including BMP,GIF,JPEG,PNG,TIFF, EXIF Wait.
There should be pictures in the bitmap
bitmap = new Bitmap(picBoxCanvas.Width, picBoxCanvas.Height)
Path.GetExtension Returns the extension in the specified path
If the suffix is bmp .png .jpeg .jpg .gif can be saved
File saving and opening:
namespace Fractal
{
class FileManager
{
public void SaveFileAsBitmap(System.Windows.Forms.PictureBox picBoxCanvas, String filename)
{
using (var bitmap = new Bitmap(picBoxCanvas.Width, picBoxCanvas.Height))
{
picBoxCanvas.DrawToBitmap(bitmap, picBoxCanvas.ClientRectangle);
ImageFormat imageFormat = null;
var extension = Path.GetExtension(filename);
switch (extension)
{
case ".bmp":
imageFormat = ImageFormat.Bmp;
break;
case ".png":
imageFormat = ImageFormat.Png;
break;
case ".jpeg":
case ".jpg":
imageFormat = ImageFormat.Jpeg;
break;
case ".gif":
imageFormat = ImageFormat.Gif;
break;
default:
throw new NotSupportedException(String.Format("File extension {0} is not supported", extension));
}
bitmap.Save(filename, imageFormat);
}
}
}
}
After saving:
5 display of fractal tree and other fractal graphics derived from it
Using random variables can generate some magical and beautiful trees
Strange tree
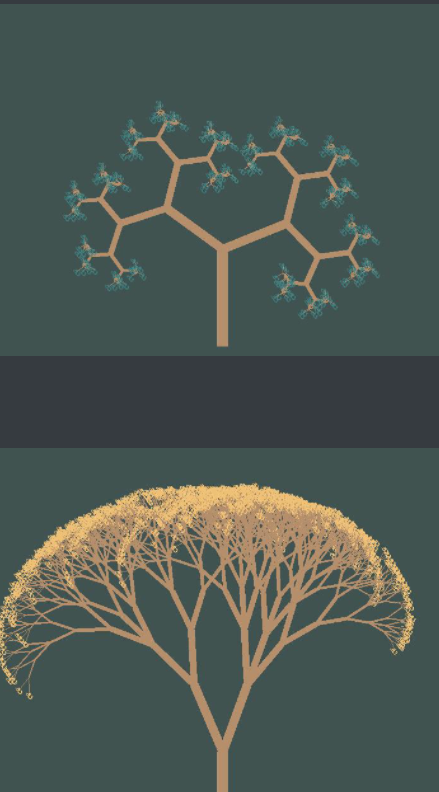
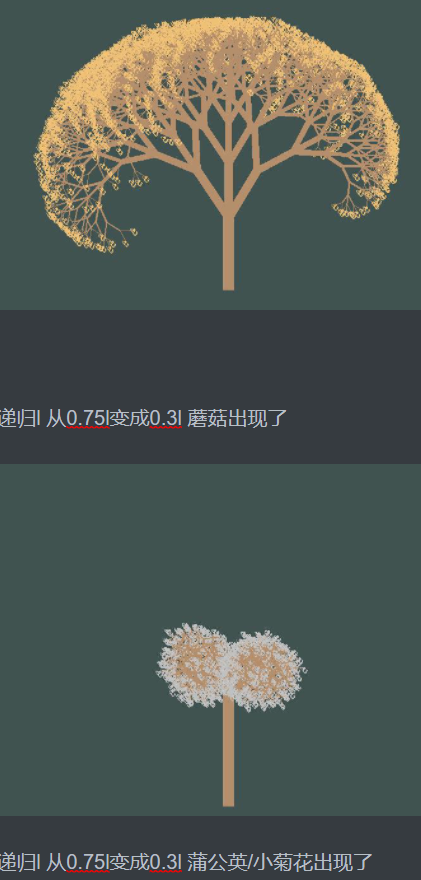
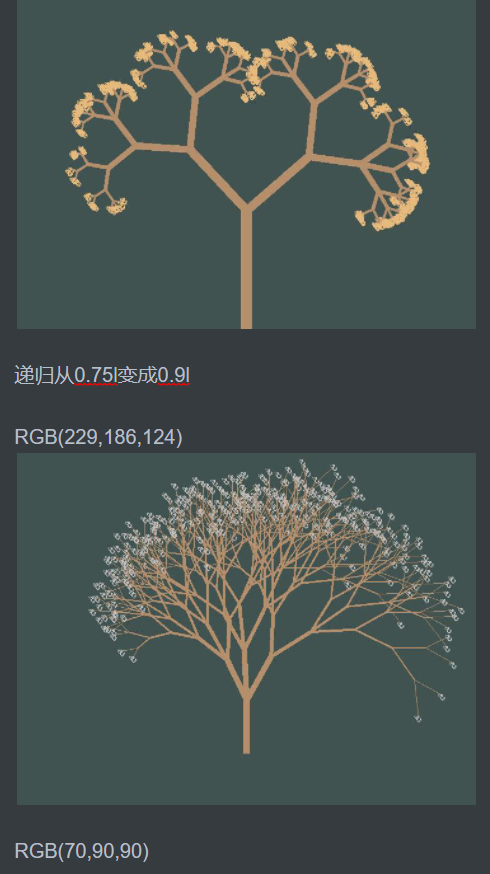

Cherry tree with falling flower effect:
//The following is the falling flower effect
//graphics.DrawArc(endLeavesPen, x1 + 20, y1 + 21, 6, 10, 0, 180);
//graphics.DrawArc(endLeavesPen, x1 + 24, y1 + 23, 6, 10, 0, 180);
//graphics.DrawArc(endLeavesPen, x1 - 27, y1 + 25, 6, 10, 0, 180);
//graphics.DrawArc(endLeavesPen, x1 - 15, y1 - 16, 6, 10, 0, 180);
//graphics.DrawArc(endLeavesPen, x1 + 20, y1 + 21, 6, 10, 0, 180);
//graphics.DrawArc(endLeavesPen, x1 - 37, y1 + 35, 6, 10, 0, 180);




4, Summary
Fractal trees use recursive methods to move from simple repetition to complexity. However, the trees created by random trees are so similar to those in nature that people can't help but imagine whether God created these trees and many things in the world with fractal algorithm