abstract
Automatic Differentiation Automatic differentiation (AD) is a technology for efficient and accurate derivation of computer programs. It has been widely used in computational fluid dynamics, atmospheric science, industrial design simulation optimization and other fields. In recent years, the rise of machine learning technology also drives the research of Automatic Differentiation technology into a new stage. With the development of Automatic Differentiation and other differentiation technologies With the deepening of research, it is more and more closely related to programming languages, computing frameworks, compilers and other fields, so as to derive and expand a more general concept of differentiable programming. This series of articles will summarize the research and development of Automatic Differentiation technology and microprogramming.
This paper will be divided into three parts, and the main framework is as follows:
- Introduction to common computer program derivation methods
- Introduction to automatic differentiation and microprogramming schemes in the industry
- Problems and prospects of automatic differentiation and microprogramming
Part I: From automatic differentiation to design of differentiable programming language (1)
Of course, if readers want to know more about the technical content related to Differentiable programming, they can continue to pay attention to the relevant articles published by SIG differentiable programming. We also welcome readers to join our programming language technology community SIG - microprogramming group to discuss microprogramming related technologies with us.
Automatic differential implementation
In the last article, we introduced the basic mathematical principle of automatic differentiation. The key steps of automatic differentiation can be summarized as follows:
- The decomposition program is a combination of basic expressions of a series of known differential rules
- The differential results of each basic expression are given according to the known differential rules
- According to the data dependency between the basic expressions, the differential results are combined by using the chain rule to complete the differential results of the program
Although the mathematical principle of automatic differentiation has been clear, the specific implementation methods can be very different. In 2018, Siskind and other scholars divided automatic differential implementation schemes into three categories in their review paper [1]:
- Basic expression method: encapsulates a series of basic expressions (such as addition, subtraction, multiplication, division, etc.) and their corresponding differential result expressions are used as library functions. Users call the library functions to build programs that need to be differentiated. The encapsulated library functions will record all basic expressions and corresponding combination relations at run time, and finally use the chain rule to combine the differential results of the above basic expressions to complete automatic differentiation.
- Operator overloading method: using the polymorphic characteristics of modern languages, operator overloading is used to encapsulate the differential rules of basic operation expressions in the language. Similarly, the overloaded operator will record all operators and corresponding combination relations at run time, and finally use the chain rule to combine the differential results of the above basic expressions to complete automatic differentiation.
- Code transformation: by extending the language preprocessor, compiler or interpreter, The basic expression differentiation rules of the program expression (such as source code, AST or IR) are predefined, and then the program expression is analyzed to obtain the combination relationship of the basic expression. Finally, the chain rule is used to combine the differentiation results of the above basic expressions to generate a new program expression corresponding to the differentiation results to complete the automatic differentiation.
Taking a = (x + y) / z as an example, three implementation methods of automatic differentiation are introduced and their advantages and disadvantages are analyzed.
Basic expression method
Taking the automatic differential implementation method [2] proposed by Wengert et al. In 1964 as an example, the user first needs to manually decompose the above function into the combination of basic expressions in the library function:
t1 = x + y a = t1 / z
Use the given library function to complete the programming of the above functions:
// The parameters are the variables x,y,t1 and the corresponding derivative variables dx,dy,dt1 call ADAdd(x, dx, y, dy, t1, dt1) // The parameters are the variables t1,z,a and the corresponding derivative variables dt1,dz,da call ADDiv(t1, dt1, z, dz, a, da)
The library function defines the mathematical differential rules and chain rules of the corresponding expression:
def ADAdd(x, dx, y, dy, z, dz): z = x + y dz = dy + dx def ADDiv(x, dx, y, dy, z, dz): z = x / y dz = dx / y + (x / (y * y)) * dy
The advantages and disadvantages of the basic expression method can be summarized as follows:
- Advantages: the implementation is simple, and can be quickly implemented as a library in any language
- Disadvantages: users must use library functions for programming, and can not use language native operation expressions
Operator overloading method
Taking AutoDiff [4], an automatic differentiation library developed by Shtof et al. [3] on csharp language in 2013, as an example, the automatic differentiation library predefined a specific data structure and overloaded the corresponding basic operation operators on the data structure.
namespace AutoDiff
{
public abstract class Term
{
// Overloaded operators ` + `, ` * ` and ` / `. When these operators are called, they will pass the
// TermBuilder records the type of operation, input and output information, etc. in tape
public static Term operator+(Term left, Term right)
{
return TermBuilder.Sum(left, right);
}
public static Term operator*(Term left, Term right)
{
return TermBuilder.Product(left, right);
}
public static Term operator/(Term numerator, Term denominator)
{
return TermBuilder.Product(numerator, TermBuilder.Power(denominator, -1));
}
}
}
When the user completes the function definition using the overloaded expression in the data type, the program will record the operation type and input and output information of the corresponding expression in a tape data structure during actual execution.
using AutoDiff;
class Program
{
public static void Main(string[] args)
{
// Variable definition. Note: variable is a subtype of Term
var x = new Variable();
var y = new Variable();
var z = new Variable();
// Function definition. At this time, the operator overload will convert the corresponding expression into a tape data structure and record relevant information
var func = (x + y) / z;
// Defines the input variable value of the function
Variable[] vars = { x, y, z};
double[] values = {1, 2, -3};
// Function execution
double value = func.Evaluate(vars, values);
// Calculate the differential result of the function
double[] gradient = func.Differentiate(vars, values);
}
}
After obtaining the tape data structure, the tape will be traversed and the basic operation recorded in it will be differentiated, and the results will be combined through the chain rule to complete the automatic differentiation.
namespace AutoDiff
{
// The basic elements in Tape data structure mainly include:
// 1) Operation result
// 2) The derivative result corresponding to the operation result of the operation
// 3) Input of operation
// In addition, the calculation rules and differential rules of the operation are defined by the functions Eval and Diff
internal abstract class TapeElement
{
public double Value;
public double Adjoint;
public InputEdges Inputs;
public abstract void Eval();
public abstract void Diff();
}
internal partial class CompiledDifferentiator : ICompiledTerm
{
// tape data structure, which stores all overloaded basic operations in the program
private readonly TapeElement[] tape;
private void ReverseSweep()
{
// Some initialization operations
for (var i = 0; i < tape.Length - 1; ++i)
tape[i].Adjoint = 0;
tape[tape.Length - 1].Adjoint = 1;
// The gradient values of variables are accumulated based on the chain rule
for (var i = tape.Length - 1; i>= dimension; --i)
{
var inputs = tape[i].Inputs;
var adjoint = tape[i].Adjoint;
for(var j = 0; j < inputs.Length; ++j)
inputs.Element(j).Adjoint += adjoint * inputs.Weight(j);
}
}
// Perform the corresponding differential operation according to the differential rules of the basic elements in tape
private void ForwardSweep(IReadOnlyList<double> arg)
{
for (var i = 0; i < dimension; ++i)
tape[i].Value = arg[i];
for (var i = dimension; i < tape.Length; ++i)
tape[i].Diff();
}
// Differential entry function, the process includes:
// 1) ForwardSweep, traverse the basic elements in tape in sequence, and call the diff interface to complete the differentiation
// 2) ReverseSweep traverses the basic elements in tape in reverse order, and accumulates the gradient results corresponding to the variables based on the chain rule
public double Differentiate(IReadOnlyList<double> arg, IList<double> grad)
{
ForwardSweep(arg);
ReverseSweep();
for (var i = 0; i < dimension; ++i)
grad[i] = tape[i].Adjoint;
return tape[tape.Length - 1].Value;
}
}
}
The advantages and disadvantages of operator overloading can be summarized as follows:
Advantages: it is simple to implement and only requires the language to provide polymorphic features and capabilities
Disadvantages:
- It is necessary to explicitly construct tape data structure and read-write operations on tape. The introduction of these additional data structures and operations is not conducive to the implementation of high-order differentiation
- For some control flow expressions such as if and while, it is usually difficult to define differential rules through operator overloading. The processing of these operations will degenerate into the encapsulation of specific functions in basic expression methods, and the language native control flow expression cannot be used
Code transformation method
Take the automatic differential library tangent [5] developed by Shtof et al. On python language in 2013 as an example. At runtime, the automatic differentiation library analyzes and obtains the AST expression of python program. Then, the decomposition and differentiation of basic expressions are completed based on AST, and then the dependencies between basic expressions are obtained by traversing AST, so as to complete automatic differentiation by using chain rule.
# Functions that need to be differentiated def f(x): return x * x # Differential result function obtained by code transformation def dfdx(x, by=1.0): _bx = tangent.unbroadcast(by * x, x) _bx2 = tangent.unbroadcast(by * x, x) bx = _bx bx = tangent.add_grad(bx, _bx2) return bx
 The advantages and disadvantages of code transformation method can be summarized as follows:
The advantages and disadvantages of code transformation method can be summarized as follows:
advantage:
- Support more data types (native data types and user-defined data types) and native language operations (basic mathematical operation operations and control flow operations)
- There is no additional tape data structure and tape read-write operation, which is conducive to the realization of high-order differentiation
- The differential result exists in the form of code, which is conducive to debugging
Disadvantages:
- The implementation is complex and requires a preprocessor, compiler or interpreter to extend the language
- It supports more data types and operations. Although the user has a higher degree of freedom, it is easier to write unsupported codes, resulting in errors. A stronger check alarm system is required
Microprogrammable
With the evolution of automatic differentiation technology and its wide application in scientific computing, artificial intelligence and other fields, the industry has gradually developed the concept of microprogrammable [6]. In microprogramming, a key idea is to deeply integrate automatic differentiation technology with tool chains such as language design, compiler / interpreter and even IDE, and take differentiation as the first-class feature in the language, so as to improve programming ease of use, performance and security:
- More language native features can be used, including various control flow expressions and more complex features such as OO
- Users can customize differentiation rules more freely to perform performance tuning or support "differentiation" of traditional non differentiable data types and operations
- It supports high-order differential and some corresponding performance optimization algorithms
- The compiler / interpreter provides a perfect check alarm system to identify and alarm codes that do not comply with the automatic differentiation rules of the current system
- Provide better automatic differential debugging capability, such as intermediate gradient value output, single-step debugging, etc
Next, we will take Swift for TensorFlow as an example to introduce the exploration and evolution of the above aspects in the industry.
Swift for TensorFlow
Swift for TensorFlow [7] is an open source project launched by Google in 2018. It aims to combine swift language and TensorFlow to build a next-generation machine learning development platform. One of the biggest highlights of the project is that the extension in swift language provides the native automatic differentiation feature. Unfortunately, the project was declared obsolete in 2021, but its work on native automatic differentiation of language will move into Swift's official community and continue to evolve.
Swift for TensorFlow project has made a lot of exploration on the integration of automatic differentiation and language design, and produced many excellent microprogrammable design concepts. Swift for TensorFlow abstracts the mathematical concepts in automatic differentiation, and provides the language elements formed after abstraction to users through a series of interfaces at the language level, so as to facilitate them to customize the corresponding automatic differentiation rules on demand.
Abstract element 1: differentiated protocol
In the traditional automatic differential implementation, the differentiable data types are usually limited to floating-point data types (such as float16, float32, float64, etc.) or specified floating-point data combination types (such as tensor, array, etc.). It is difficult for users to customize the required differentiable data types by using the common combined data types such as struct, record, class, etc. in the programming language.
Swift for TensorFlow abstracts the differential rules of data into the differential protocol structure in swift language [8], Then, for any data type (including user-defined data types and non differentiable types in the traditional sense, such as String), you only need to inherit and implement the interface in the differential protocol to encapsulate it as a legal differentiable data type.
public protocol Differentiable {
// Defines the gradient type corresponding to the current data type
associatedtype TangentVector: Differentiable & AdditiveArithmetic
where TangentVector == TangentVector.TangentVector
// Defines how gradient type data acts on the original data type (usually used for data update based on gradient values)
mutating func move(by offset: TangentVector)
}
// Array type inherits differential protocol and becomes a legal differentiable type
extension Array: Differentiable where Element: Differentiable {
// Gradient of Array type data or Array type
public struct TangentVector: Differentiable, AdditiveArithmetic {
public typealias TangentVector = Self
@differentiable
public var elements: [Element.TangentVector]
@differentiable
public init(_ elements: [Element.TangentVector]) { self.elements = elements }
...
}
// The gradient based data update method updates each element in the Array recursively
public mutating func move(by offset: TangentVector) {
for i in indices {
self[i].move(by: Element.TangentVector(offset.elements[i]))
}
}
}
Abstract element 2: differentiated attribute
Although in some other automatic differential implementations, The user also specifies the program fragments (usually functions) that need to be differentiated in the syntax form of annotations or attributes. However, Swift for TensorFlow integrates the @ differential attribute [9] it provides with the language type system and automatic differentiation rules, providing users with an easy-to-use and highly free programming interface:
- You can customize whether the function needs to be differentiated and which inputs of the function need to be differentiated through @ differentiated attribute
- The user can manually provide the differentiation result of the function through @ differentiated attribute to replace the built-in differentiation rules of the compiler
// Specifies that the cubed function needs to be differentiated
@differentiable
func cubed(_ x: Float) -> Float {
x * x * x
}
// Specifies that the sly function needs to be differentiated, and only the partial differentiation of input x is considered
@differentiable(wrt: x)
func silly(_ x: Float, _ n: Int) -> Float {
print("Running'silly'on \(x) and \(n)!")
return sin(cos(x))
}
extension FloatingPoint
where Self: Differentiable & AdditiveArithmetic, Self == TangentVector
{
// Manually specify the differential result of ` + ` operator function in FloatingPoint type
@transpose(of: +)
static func _(_ v: Self) -> (Self, Self) { (v, v) }
}
Abstract element 3: differentiated type
In Swift for TensorFlow, when the user uses the above interface to specify the data types and program fragments that need to be differentiated, their types will also be changed accordingly. Swift for TensorFlow extends the type system of swift language, and establishes the subtype relationship between types and differentiable types by using the concept of subtype, so as to complete some automatic differential rule checking by using the native type rule checking ability of swift language.
Take the function type as an example. When the user specifies that the function is differentiable, its type will become a differentiable function type, which is a subtype of the original function type. Furthermore, Swift for TensorFlow also subdivides differentiable function types into linear differentiable function types (Note: this definition involves a large number of differential mathematical concepts, which will not be expanded in detail in this paper. Interested readers can refer to the official Swift for TensorFlow document).
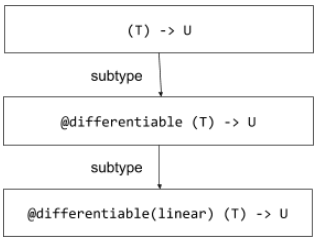
After defining the type relationship, you can check it through standard type rules, such as whether the types match, allowing any up cast between types, allowing down cast of types only under specific circumstances, and so on.
func addOne(_ x: Float) -> Float { x + 1 }
let _: @differentiable (Float) -> Float = addOne // Okay!
let _: @differentiable(linear) (Float) -> Float = addOne // Okay!
let _: @differentiable(linear) (Float) -> Float = coshf(_:)
// Error: `coshf(_:)` is from a different module and has not been marked with
// `@differentiable`.
func mySin(_ x: Float) -> Float { sin(x) * 2 }
let _: @differentiable (Float) -> Float = mySin // Okay!
let _: @differentiable(linear) (Float) -> Float = mySin
// Error: When differentiating `mySin(_:)` as a linear map, `sin` is not linear.
func addOneViaInt(_ x: Float) -> Float { Float(Int(x) + 1) }
let _: @differentiable (Float) -> Float = addOneViaInt
// Error: When differentiating `addOneViaInt(_:)`, `Int(x)` is not differentiable.
Meanwhile, Swift for TensorFlow has also done a lot of practice and exploration in the direction of OO feature support, debugging and high-order differentiation. It is recommended that interested readers further read the relevant official document chapters.
In addition, there are also excellent general or domain specific microprogrammable design schemes in the industry, including Julia zygote [10], TaiChi [11]. We will not start one by one here. Interested readers can go to the relevant official communities to learn about them.
Next Trailer
With the evolution of technology and the demand transformation in the application field, the implementation of automatic differentiation, from basic expression method to operator overloading and then to code transformation, reflects the increasing importance of differentiation in specific field programming. The concept of microprogramming came into being under this background. Although the industry has explored excellent projects such as Swift for TensorFlow, the design of microprogramming language is far from perfect, and there are still many problems to be solved. In the next section, we will focus on summarizing some current technical challenges in the field of differentiable programming and the prospect of the next work.
reference
[1] Atilim Gunes Baydin, Barak A. Pearlmutter, and Alexey AndreyevichRadul. Automatic differentiation in machine learning: a survey. CoRR, abs/1502.05767, 2015. https://arxiv.org/abs/1502.05767
[2] R. E. Wengert. A simple automatic derivative evaluation program.Commun.ACM, 7(8):463–464, August 1964. https://dl.acm.org/doi/abs/10.1145/355586.364791
[3] A. Shtof, A. Agathos, Y. Gingold, A. Shamir, and D. Cohen-Or. Geosemanticsnapping for sketch-based modeling. Computer Graphics Forum, 32(2pt2):245–253, 2013. https://doi.org/10.1111/cgf.12044
[4] AutoDiff: A .NET library that provides fast, accurate and automatic differentiation (computes derivative / gradient) of mathematical functions. https://github.com/alexshtf/autodiff
[5] Tangent: Source-to-Source Debuggable Derivatives in Pure Python. https://github.com/google/tangent
[6] Differentiable Programming - Wikipedia: https://en.wikipedia.org/wiki/Differentiable_programming
[7] Swift for TensorFlow https://www.tensorflow.org/swift/guide/overview
[8] Swift Differentiable Programming Manifesto: The Differentiable protocol. https://github.com/apple/swift/blob/main/docs/DifferentiableProgramming.md#the-differentiable-protocol
[9] Swift Differentiable Programming Manifesto: The @differentiable declaration attribute. https://github.com/apple/swift/blob/main/docs/DifferentiableProgramming.md#the-differentiable-declaration-attribute
[10] Zygote https://fluxml.ai/Zygote.jl/latest/
[11] Taichi: A High-Performance Programming Language for Computer Graphics Applications. https://github.com/taichi-dev/taichi
