All the code in this article is big root heap! The implementation language is Java

The pictures are all from the great God, and the great God's articles also give me a lot of inspiration Heap of data structures

Heap sort This video is easy to understand, from what is heap, what is heap, and then to the realization of heap sorting. It is very clear. The implementation language is C

What is a heap

1. Concept of reactor

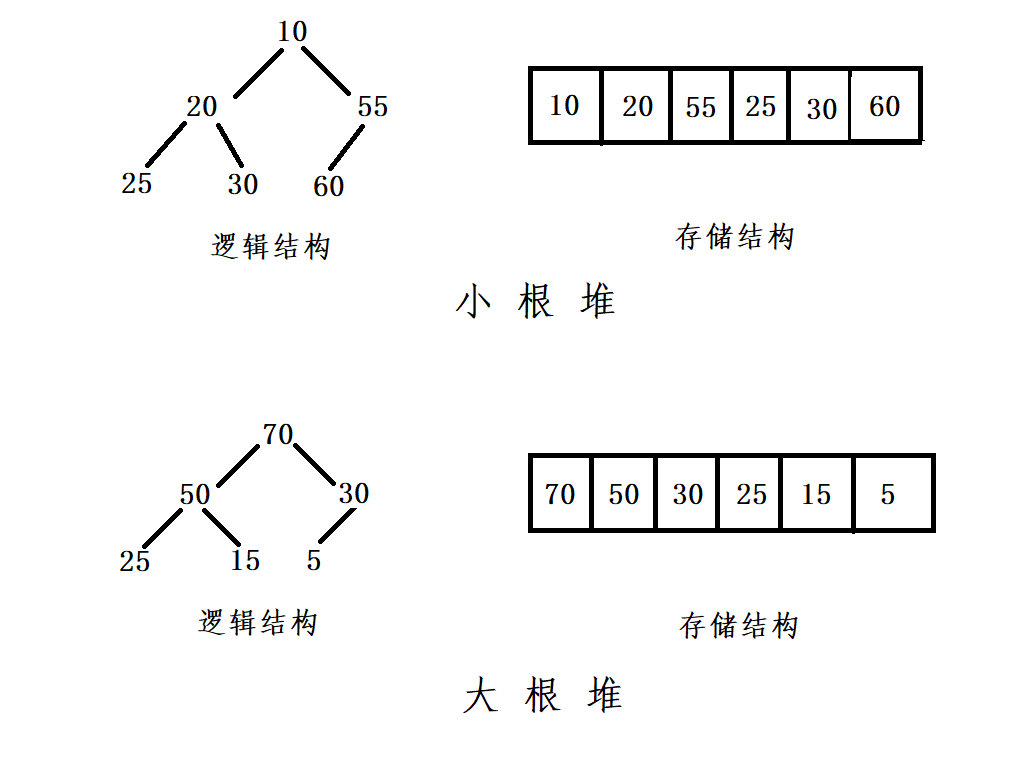
If there is a key set K = {k0, k1, k2,..., kn-1}, all its elements are stored in a one-dimensional array in the order of a complete binary tree and meet the following requirements: ki < = k2i + 1 and Ki < = k2i + 2, it is called a small heap (or a large heap).

The heap with the largest root node is called the maximum heap or large root heap, and the heap with the smallest root node is called the minimum heap or small root heap.

2. Nature

1. Heap is a complete binary tree
2. A node in the heap is not greater than or less than the value of its parent node

3. Relationship between binary tree and heap

Now that we know that the logical structure of the heap conforms to the property of a complete binary tree, the heap conforms to the property of a complete binary tree. There are two properties here. The next learning of the heap is very important!!

In the heap, if cur represents the subscript of the current node, parent represents the subscript of its parent node, and child1 and child2 represent the subscripts of its two child nodes, then

1. parent = (cur - 1) / 2
2. child1 = 2 * i + 1
3. child2 = 2 * i + 2

How to implement heap?

Knowing that the heap is composed of arrays, how can the array become the heap we want? Here is a method of heap!

heapify heap, an algorithm that converts an array into a heap! Other blogs also call it up adjustment algorithm and down adjustment algorithm.

The upward adjustment algorithm is based on the downward adjustment algorithm, so to understand the upward adjustment, you must first understand what is downward adjustment, which is also a difficulty!

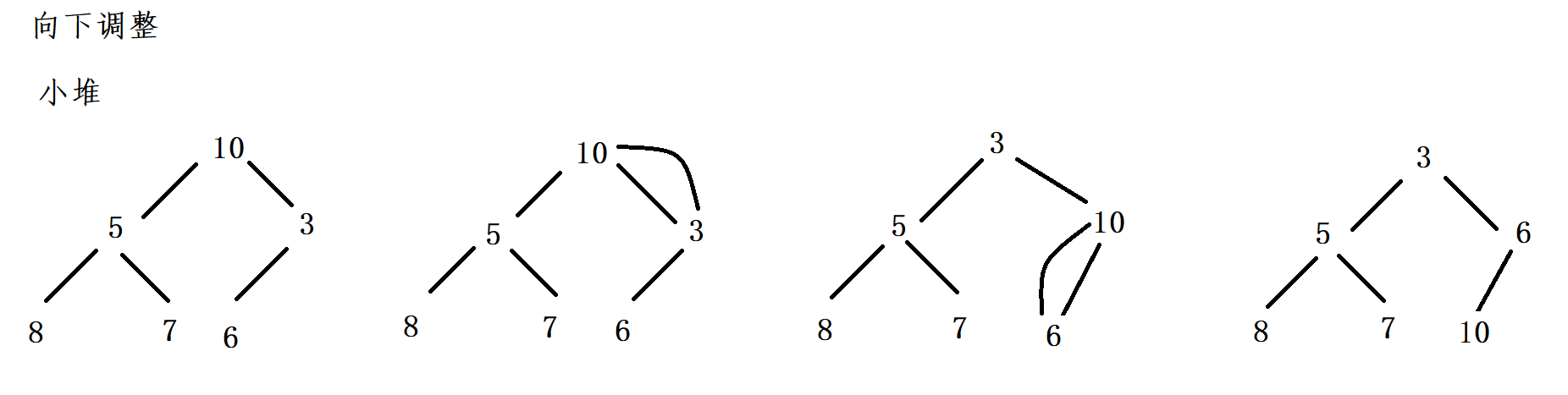
Principle of downward adjustment algorithm

1. Set the root node as the current node (obtained by subscript and marked as cur), compare the values of the left and right subtrees, find out the smaller values, and mark them with child.
2. Compare the values of child and cur. If child is smaller than cur, it does not meet the rule of small heap and needs to be exchanged.
3. If the child is larger than cur and meets the rule of small heap, no exchange is required, and the adjustment is completed.
4. After processing a node, start from the current child and cycle the previous process.

The downward adjustment algorithm is based on the original heap, which is not the heap due to the insertion of elements

The example in the figure also shows that 587 is a small root heap that meets the conditions

Principle of upward adjustment algorithm

1. First, set the penultimate leaf node as the current node (obtained by subscript and marked as cur), find its parent node and mark it with parent.
2. Compare the values of parent and cur. If cur is smaller than parent, it does not meet the rule of small heap and needs to be exchanged.
3. If the cur is larger than the parent and meets the rule of small heap, no exchange is required, and the adjustment is completed.
4. After processing a node, start from the current parent and cycle the previous process.

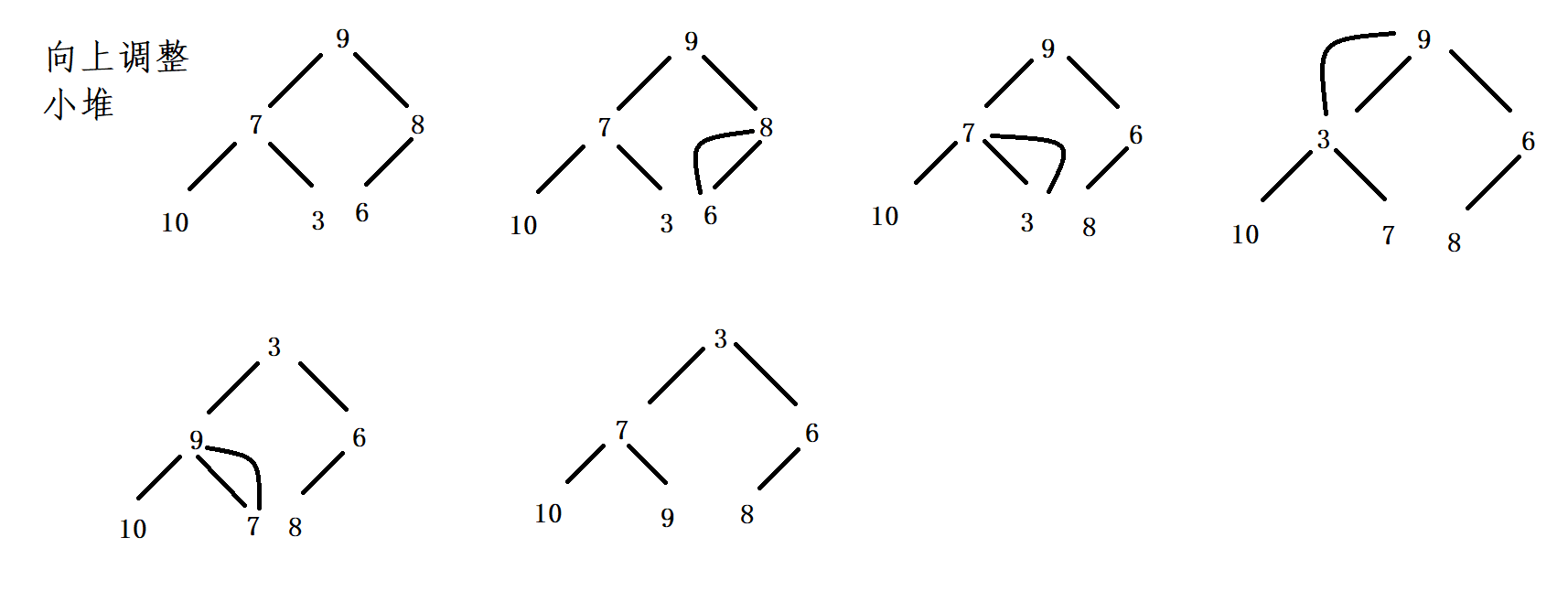
The upward adjustment algorithm mentioned above is based on the downward adjustment algorithm! Why do you say that? Because the process of upward adjustment is to divide the binary tree into minimum units (the minimum unit here refers to the minimum binary tree composed of one root node zero to two child nodes), and make a downward adjustment algorithm for each minimum binary tree from bottom to top. When the downward adjustment algorithm is completed for all the minimum binary trees, the heap is completed!

After we understand what heap is, let's start to implement it. The recursive method is used here

Recursion is a little difficult to understand here. Let me say it alone, because we pass in the array. The i traversed for the first time represents the top element of the heap, from top to bottom until it touches the leaf node

/**
     * Exchange two values. Note that bit operation cannot be used here because the first element of the array will be 0
     *
     * @param array array
     * @param i     First value
     * @param j     Second value
     */
public static void swap(int[] array, int i, int j) {
    int temp = array[i];
    array[i] = array[j];
    array[j] = temp;
}

//Heap is composed of up adjustment algorithm and down adjustment algorithm

/**
     * Downward adjustment algorithm
     *
     * @param tree The storage structure is an array and the logical structure is a complete binary tree
     * @param size Array length
     * @param i    Parent node
     */
public static void heapify(int[] tree, int size, int i) {
    //Record the parent node for subsequent exchange
    int max = i;
    //Two child nodes of the parent node
    int child1 = 2 * i + 1;
    int child2 = 2 * i + 2;
    //If the left child is larger than the parent node, record the left child node
    if (child1 < size && tree[child1] > tree[max]) {
        max = child1;
    }
    //If the right child is larger than the parent node or the left node (the left child was recorded in the previous if judgment true), the right child is recorded
    if (child2 < size && tree[child2] > tree[max]) {
        max = child2;
    }
    if (max != i) {
        swap(tree, max, i);
        heapify(tree, size, max);
    }
}

/**
     * The up adjustment algorithm builds an unordered array into a heap
     *
     * @param tree array
     * @param size Array size
     */
public static void buildHeap(int[] tree, int size) {
    //Adjust the algorithm from bottom to top, starting from the last node
    int lastNode = size - 1;
    //The parent node of this node
    int parent = (lastNode - 1) / 2;
    for (int i = parent; i >= 0; i--) {
        //Downward adjustment algorithm for each minimum unit
        heapify(tree, size, i);
    }
}

I don't understand recursion, and it doesn't matter. There are iterations here

public static void heapify(int[] tree, int size, int i) {
    //Left and right children of the current node
    int child1 = 2 * i + 1;
    int child2 = 2 * i + 2;
    //The traversal to the leaf node is over
    while (child1 < size) {
        int max = i;
        //If the left child is larger than the parent node, record the left child node
        if (child1 < size && tree[child1] > tree[max]) {
            max = child1;
        }
        //If the right child is larger than the parent node or the left node (the left child was recorded in the previous if judgment true), the right child is recorded
        if (child2 < size && tree[child2] > tree[max]) {
            max = child2;
        }
        //If the parent node index is the maximum index, it is already a large root heap, then exit the loop
        if (i == max) {
            break;
        }
        //The parent node is not the maximum value and is exchanged with the larger value in the child
        swap(tree, max, i);
        //Point the index to the index of the larger value in the child
        i = max;
        //Recalculate the index of the child after the exchange
        child1 = 2 * i + 1;
        child2 = 2 * i + 2;
    }
}

After understanding the heap (downward adjustment), I believe you feel closer and closer to the heap

Heap sort

After understanding the heap construction process, heap sorting should not be too simple. Let's directly talk about the implementation principle of the algorithm

1. Construct the sequence to be sorted into a large root heap
2. At this point, the maximum value of the whole sequence is the root node at the top of the heap.
3. Swap it with the end element, where the end is the maximum.
4. Then reconstruct the remaining n-1 elements into a heap, which will get the sub small value of n-1 elements. If you execute it repeatedly, you can get an ordered sequence.

The complete code is posted here

/**
 * Heap sort
 *
 * @author ccy
 * @version 1.0
 * @date 2021/11/20 15:11
 */
public class HeapSort {
    /**
     * Exchange two values. Note that bit operation cannot be used here because the first element of the array will be 0
     *
     * @param array array
     * @param i     First value
     * @param j     Second value
     */
    public static void swap(int[] array, int i, int j) {
        int temp = array[i];
        array[i] = array[j];
        array[j] = temp;
    }

    //Heap is composed of up adjustment algorithm and down adjustment algorithm

    /**
     * Downward adjustment algorithm
     *
     * @param tree The storage structure is an array and the logical structure is a complete binary tree
     * @param size Array length
     * @param i    Parent node
     */
    public static void heapify(int[] tree, int size, int i) {
        //Record the parent node for subsequent exchange
        int max = i;
        //Two child nodes of the parent node
        int child1 = 2 * i + 1;
        int child2 = 2 * i + 2;
        //If the left child is larger than the parent node, record the left child node
        if (child1 < size && tree[child1] > tree[max]) {
            max = child1;
        }
        //If the right child is larger than the parent node or the left node (the left child was recorded in the previous if judgment true), the right child is recorded
        if (child2 < size && tree[child2] > tree[max]) {
            max = child2;
        }
        if (max != i) {
            swap(tree, max, i);
            heapify(tree, size, max);
        }
    }

    /**
     * The up adjustment algorithm builds an unordered array into a heap
     *
     * @param tree array
     * @param size Array size
     */
    public static void buildHeap(int[] tree, int size) {
        //Adjust the algorithm from bottom to top, starting from the last node
        int lastNode = size - 1;
        //The parent node of this node
        int parent = (lastNode - 1) / 2;
        for (int i = parent; i >= 0; i--) {
            //Downward adjustment algorithm for each minimum unit
            heapify(tree, size, i);
        }
    }

    /**
     * Heap sort
     *
     * @param tree Array to be sorted
     * @param size Array length
     */
    public static void heapSort(int[] tree, int size) {
        buildHeap(tree, size);
        for (int i = size - 1; i >= 0; i--) {
            swap(tree, i, 0);
            heapify(tree, i, 0);
        }
    }

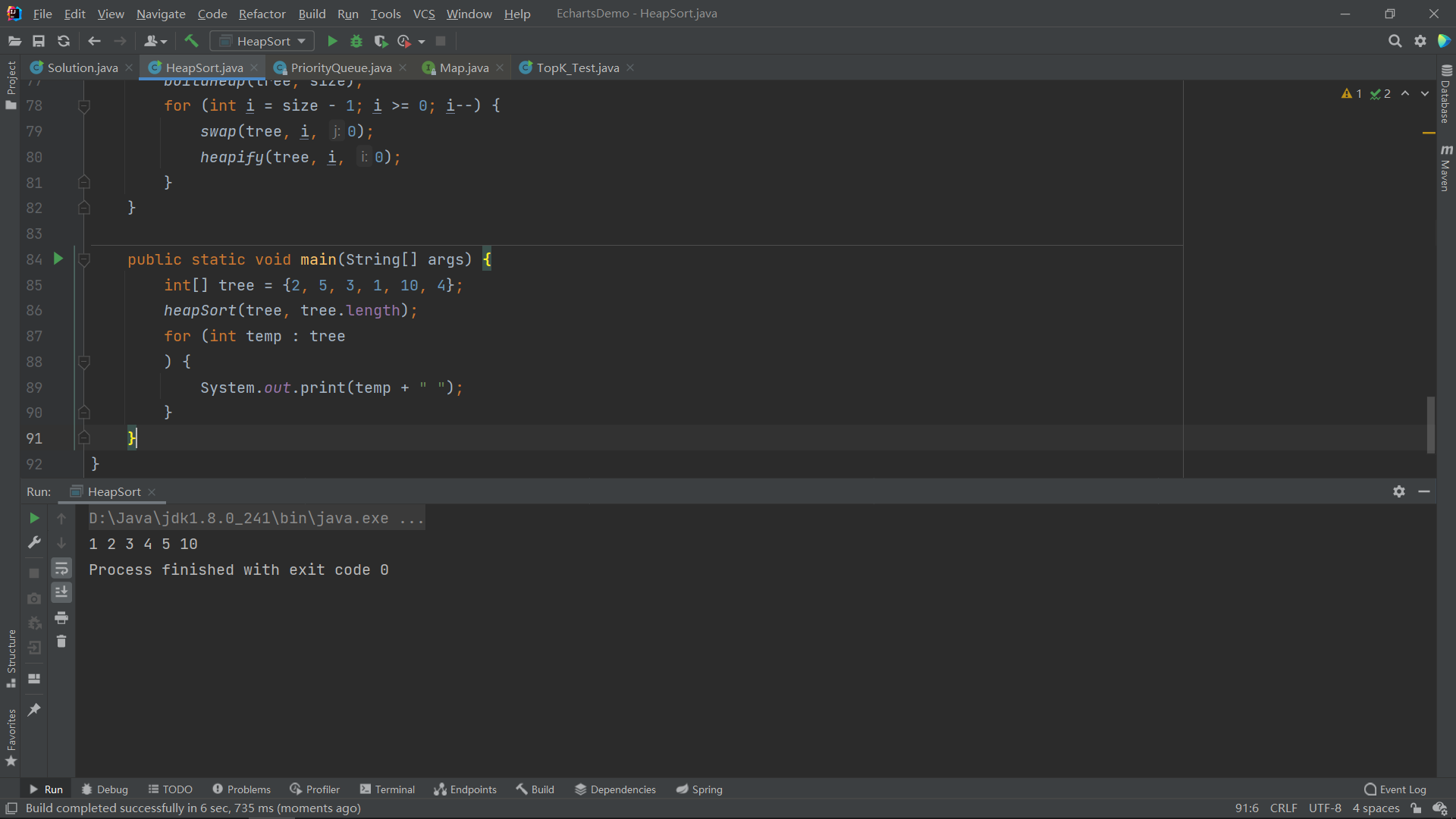
    public static void main(String[] args) {
        int[] tree = {2, 5, 3, 1, 10, 4};
        heapSort(tree, tree.length);
        for (int temp : tree
            ) {
            System.out.print(temp + " ");
        }
    }
}

Priority queue

Here, the article introduces a low-level priority queue implemented by heap, which sorts the added elements by rewriting the compare method,

PriorityQueue is an unbounded queue based on priority heap. The elements in this priority queue can be sorted naturally by default or through the provided
Comparator sorts when the queue is instantiated.

PriorityQueue does not allow null values, and does not support non comparable objects, such as user-defined classes. Priority queues require the use of Java Comparable and Comparator interfaces to sort objects, and the elements in them will be processed according to priority when sorting.

The size of PriorityQueue is unlimited, but the initial size can be specified at creation time. When we add elements to the priority queue, the queue size will increase automatically.

PriorityQueue is non thread safe, so Java provides PriorityBlockingQueue (implementing the BlockingQueue interface) for Java multithreading environment.