Writing this article stems from a previous interview and from various examples on the Internet that native sort s are faster than fast queues, because they have not written fast queues well. I was asked to write a quick line during the interview. I wrote a very concise piece of code that I read online (which I later found was in the JavaScript Description of Data Structure and Algorithms There are also in this book:

function quickSort(arr){
    if(arr.length < 1){
            return [];
    }
    var left = [],right = [],flag = arr[0];
    for(var i=1;i<arr.length;i++){
        if(arr[i] <= flag){
            left.push(arr[i]);
        }else{
            right.push(arr[i]);
        }
    }
    return quickSort(left).concat(flag,quickSort(right));
}

In this way, at first glance, it is a fast-paced idea. It puts elements smaller than principal elements in the left array, elements larger than principal elements in the right array, and then sorts the elements of left and right arrays separately, and finally splices them into new arrays.
But this is not how fast scheduling is explained in computer courses. One-time fast sorting algorithms are generally described in this way:

1. Set two variables i and j to start the sorting: i=0, j=N-1;

2. With the first array element as the key data, the key is assigned, that is, key=A[0].

3. Search forward from j, that is, search forward from back (j--), find the first value A[j], which is less than key, and exchange A[j] and A[i];

4. Search backward from i, that is, search backward from front (i++), find the first A[i] larger than the key, and exchange A[i] and A[j];

5. Repeat steps 3 and 4 until i=j.

The version implemented with js is as follows:

function quickSort_two(arr){
    function sort(start,end){
        if(start + 1 > end){
            return;
        }
        var flag = arr[start],f = start,l = end;
        while(f < l){
            while(f < l && arr[l] > flag){
                l--;
            }
            arr[f] = arr[l];
            while(f < l && arr[f] <= flag){
                f++;
            }
            arr[l] = arr[f];
        }
        arr[f] = flag;
        sort(start,f-1);
        sort(f+1,end);   
    }
    sort(0,arr.length-1);
}

Comparing the two fast-paced schemes, the time complexity is O(nlogn), but the second one uses less space. The space complexity of the first one is O(nlogn), while the space complexity of the second one is O(logn), and the operation of the array is done on the original array, which subtracts the consumption of space and time to create, and undoubtedly improves the performance more.

The following is a comparison of the three sorting algorithms:

function quickSort_one(arr){
    if(arr.length < 1){
            return [];
    }
    var left = [],right = [],flag = arr[0];
    for(var i=1;i<arr.length;i++){
        if(arr[i] <= flag){
            left.push(arr[i]);
        }else{
            right.push(arr[i]);
        }
    }
    return quickSort_one(left).concat(flag,quickSort_one(right));
}

function quickSort_two(arr){
    function sort(start,end){
        if(start + 1 > end){
            return;
        }
        var flag = arr[start],f = start,l = end;
        while(f < l){
            while(f < l && arr[l] > flag){
                l--;
            }
            arr[f] = arr[l];
            while(f < l && arr[f] <= flag){
                f++;
            }
            arr[l] = arr[f];
        }
        arr[f] = flag;
        sort(start,f-1);
        sort(f+1,end);   
    }
    sort(0,arr.length-1);
}

function quickSort_three(arr){
    arr.sort(function(a,b){
        return a-b;
    });
}

function countTime(fn,arr){
    var start = Date.now();
    fn(arr);
    var end = Date.now();
    console.log(end - start);
}

function randomVal(num){
    var arr = [];
    for(var i=0;i<num;i++){
        arr.push(Math.ceil(Math.random()*num));
    }
    return arr;
}

In the case of chrome (in the case of 100,000 arrays, new arrays are created each time because the array changes after each sorting, and the results are worth referring to if they are not the same arrays, based on 100,000 cardinals):

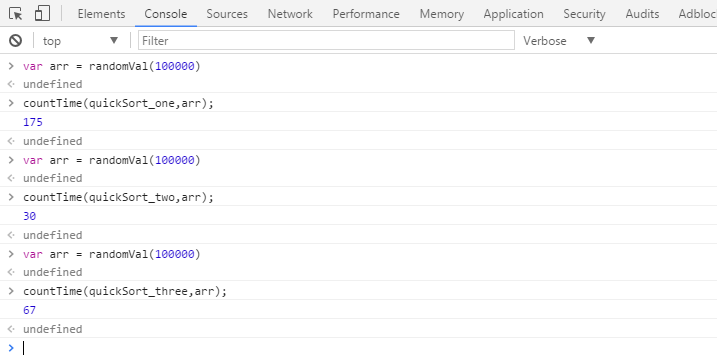
Running results under firefox:

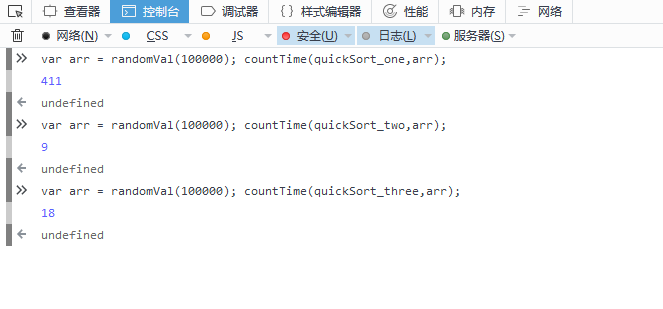
Whether it's firefox or chrome, the first sort algorithm takes the longest time, the second one is the fastest, and the native sort method is a little slower than the second one, but much faster than the first one.