Content:
- Full Permutation implementation
- Eight queens combined with full arrangement
- Optimization of eight queens backtracking method by Full Permutation
- The realization of eight queens by complete backtracking
- Summary: divide and conquer and recursion
1. Full Permutation implementation
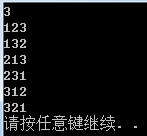
Output a 1~n permutation. For example: 1 to 3122313221321312321
Algorithm description:
- Set an array p[maxn] to store the fully arranged numbers;
- Set an array hashTable[maxn] to mark whether the element has been stored in p []. The type is bool, and the return values are true and false;
- The first loop enumerates 1 to n. when the element is not marked, that is, it is not stored in the array p, the next step is performed;
- The element is stored i n the p array, that is, p[index]=i; the variable index represents the insertion position. At this time, the outer loop 1~n has stored 1~n in p[1](index=1);
- At this time, element i needs to be marked as inserted element, that is, hashTable[x]=true;
- After processing the index bit, start processing the index+1 bit, i.e. generate P (index+1). Remember that the inserted element follows the function execution at this time;
- After dealing with index+1, element x needs to restore the state for the next step of the for loop.
#include<iostream>
using namespace std;
const int maxn = 11;
int n,p[maxn], hashTable[maxn] = { false };
void generateP(int index) {
//Recursive boundary
if (index == n + 1) {
for (int i = 1;i <= n;i++) {
cout << p[i];
}
cout << endl;
return;
}
//Enumerate 1~n to store element x in p[index]
for (int x = 1;x <= n;x++) {
if (hashTable[x] == false) {
p[index] = x;
hashTable[x] = true;
generateP(index+1);
hashTable[x] = false;
}
}
}
int main() {
cin >> n;
generateP(1);
system("pause");
return 0;
}Execution result:
2. Eight queens combined with full arrangement
Eight Queen's questions:
In an 8 * 8 chessboard, there can only be one queen in each row and column, otherwise it will be eaten by the existing queen. The queen can eat the new queen in the same row, column and diagonal.
Analysis:
After thinking, it is not difficult to find the fact that there is exactly one queen in each row and column. If the p[] array is used to represent the column number of the queen in row index, the problem becomes the problem of Full Permutation generation. The rest is to rule out the same diagonal results.
Exclude the same diagonal:
int count = 0;//Record the result of meeting the eight queens
if (index == n + 1) {
bool flag = true;
for (int i = 1;i <= n;i++) {
for (int j = i + 1;j <= n;j++) {
if (abs(i - j) == abs(p[i] - p[j])) {//The same absolute value means the same diagonal
flag = false;
}
}
}
if (flag)
count++;
return count;
}
Preliminary code implementation:
#include<iostream>
#include<stdlib.h>
#include<cmath>
using namespace std;
const int maxn = 11;
int n, p[maxn], hashTable[maxn] = { false };
int generateP(int index) {
//Recursive boundary
int count = 0;
if (index == n + 1) {
bool flag = true;
for (int i = 1;i <= n;i++) {
for (int j = i + 1;j <= n;j++) {
if (abs(i - j) == abs(p[i] - p[j])) {
flag = false;
}
}
}
if (flag)
count++;
return count;
}
//Enumerating 1~n, pre storing element x in p[index]
for (int x = 1;x <= n;x++) {
if (hashTable[x] == false) {
p[index] = x;
hashTable[x] = true;
generateP(index + 1);
hashTable[x] = false;
}
}
}
int main() {
cin >> n;
int count=generateP(1);
cout <<count<< endl;
system("pause");
return 0;
}