In fact, there are not many types of topics in dynamic programming. Here we only talk about simple DP, and the division boundary between various DP is not so obvious, so it is only a general division. It is important to learn to think.
Dynamic programming I understand: excellent state representation + no weight and no leakage state transfer. I think the most difficult thing is how to represent the state. Here is a brief introduction to some commonly used models, and then by brushing questions, I should be able to improve my level.
Time complexity of general dynamic programming = number of states * calculation amount of transfer
Knapsack model
The knapsack problem is to give you a knapsack with limited capacity, some items with certain value and will occupy a certain volume, and ask the maximum value you can get. According to the different constraints of the problem, it can be roughly divided into the following types.
01 Backpack
Example: AcWing2
As the name suggests, in the 01 knapsack problem, an item is used either 0 times or once.
We generally think about dynamic programming from two aspects: state representation + state transition.
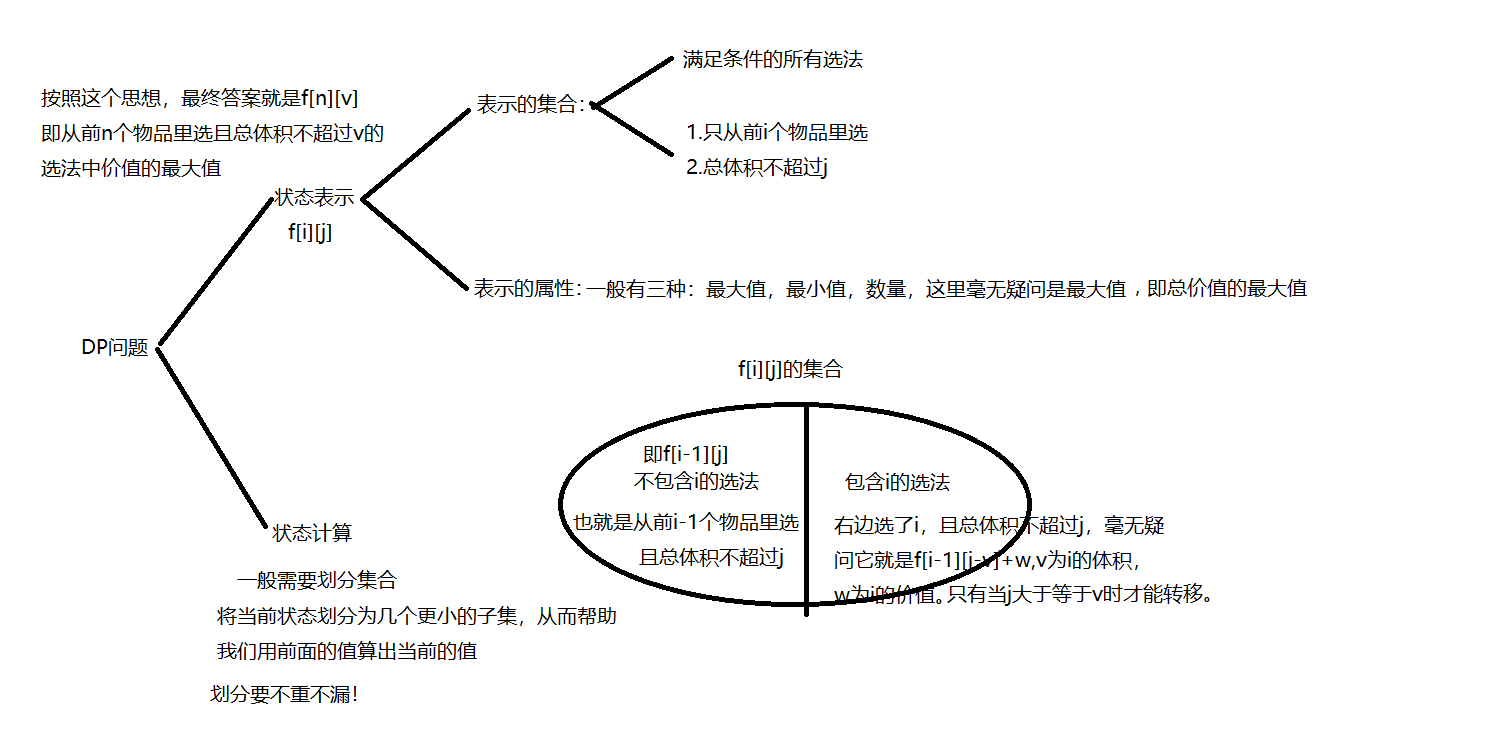
Therefore, f[i][j]=max(f[i-1][j],f[i-1][j-v]+w);
In addition, we should note that the basic situation should be considered in the dp problem. Suppose m is the total volume of the backpack, and f[0][0~m] in this question means that 0 items are considered, then it must be 0 in the end. Although there will be no error without considering this situation in this question (the global variable defaults to 0), it is likely to be wrong without considering the basic situation in some questions.
Code implementation:
#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
int v[N]; // Volume of each item
int w[N]; // Value of each item
int f[N][N]; // F [i] [J], under volume J, only the maximum value of the first I items is considered
int main() {
int n, m;
cin >> n >> m;
for(int i = 1; i <= n; i++)
cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++){
// If the i-th item cannot be loaded into the current backpack capacity, the value is equal to considering only the first i-1 item
if(j < v[i])
f[i][j] = f[i - 1][j];
// If it can be loaded, you need to make a decision whether to select the ith item
else
f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
}
cout << f[n][m] << endl;
return 0;
}
Through observation, when we calculate the ith item, we only use the attributes of i-1 item, so we can optimize it with rolling array:
#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
int v[N]; // Volume of each item
int w[N]; // Value of each item
int f[2][N]; // F [i] [J], under volume J, only the maximum value of the first I items is considered
int main() {
int n, m;
cin >> n >> m;
for(int i = 1; i <= n; i++)
cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++){
// If the i-th item cannot be loaded into the current backpack capacity, the value is equal to considering only the first i-1 item
if(j < v[i])
f[i & 1][j] = f[i - 1 & 1][j];
// If it can be loaded, you need to make a decision whether to select the ith item
else
f[i & 1][j] = max(f[i - 1 & 1][j], f[i - 1 & 1][j - v[i]] + w[i]);
}
cout << f[n & 1][m] << endl;
return 0;
}
Again, when we calculate the i-th item, we only consider the attributes of i-1 item, and when we calculate the j-volume, we use the value under the upper j-v volume. Therefore, we only use one-dimensional array, and then cycle the volume from large to small. If the volume still circulates from small to large, the j-v volume of the current layer is used to calculate the j-volume, which is wrong.
Code implementation:
#include<iostream>
using namespace std;
const int N=1e3+10;
int w[N],v[N];
int f[N];
int main(){
int n,s;
cin>>n>>s;
for(int i=1;i<=n;i++){
cin>>v[i]>>w[i];
}
for(int i=1;i<=n;i++){
for(int j=s;j>=v[i];j--){
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
cout<<f[s]<<endl;
return 0;
}
Complete Backpack
Example: AcWing3
The complete knapsack problem is similar to the 01 knapsack problem, but each item can be used unlimited times
We still think in the above way.
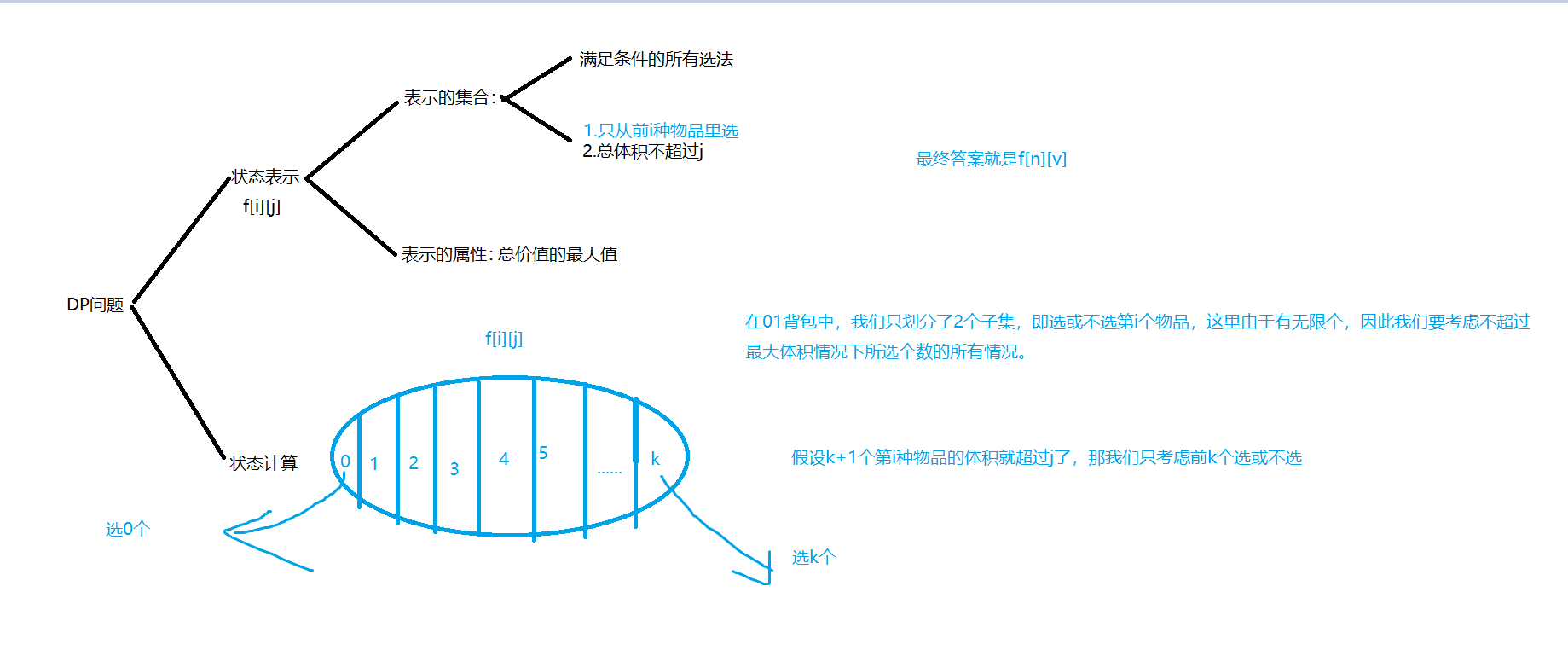
Then f[i][j]=max(f[i-1][j-x* v]+x *w),x=0,1,2... k;
In this way, our simple code can be written:
#include<iostream>
using namespace std;
const int N = 1010;
int f[N][N];
int v[N],w[N];
int main(){
int n,m;
cin>>n>>m;
for(int i = 1 ; i <= n ;i ++){
cin>>v[i]>>w[i];
}
for(int i = 1 ; i<=n ;i++){//Consider the first i items
for(int j = 0 ; j<=m ;j++){//Consider all volumes
for(int k = 0 ; k*v[i]<=j ; k++)//Consider choosing k items
f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
}
}
cout<<f[n][m]<<endl;
}
There is no doubt that the time complexity of this triple loop will be tle, so we consider optimization.
We found that:
f[i][j]=max(f[i-1][j-x* v]+x w),x=0,1,2...k;
f[i][j-v]=max(f[i-1][j-x v]+x *w),x=1,2...k;
Therefore, f[i][j]=max(f[i-1][j],f[i][j-v]+w);
Then we find that our space can also be optimized in one dimension, because we deduce the final state transition equation, which only uses the value of the same volume of the previous layer and the value of the smaller volume of the current layer. The final code:
#include<iostream>
using namespace std;
int n,s;
const int N=1010;
int v[N],w[N];
int f[N];
int main(){
cin>>n>>s;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
for(int i=1;i<=n;i++){
for(int j=v[i];j<=s;j++){
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
cout<<f[s]<<endl;
return 0;
}
Multiple backpack 1
Example: AcWing4
In the multiple knapsack problem, the number of each item is limited. You may feel: isn't it simpler? In fact, it is more complicated, but we will feel this complexity later, because the data range of this topic is not large. Analysis diagram:
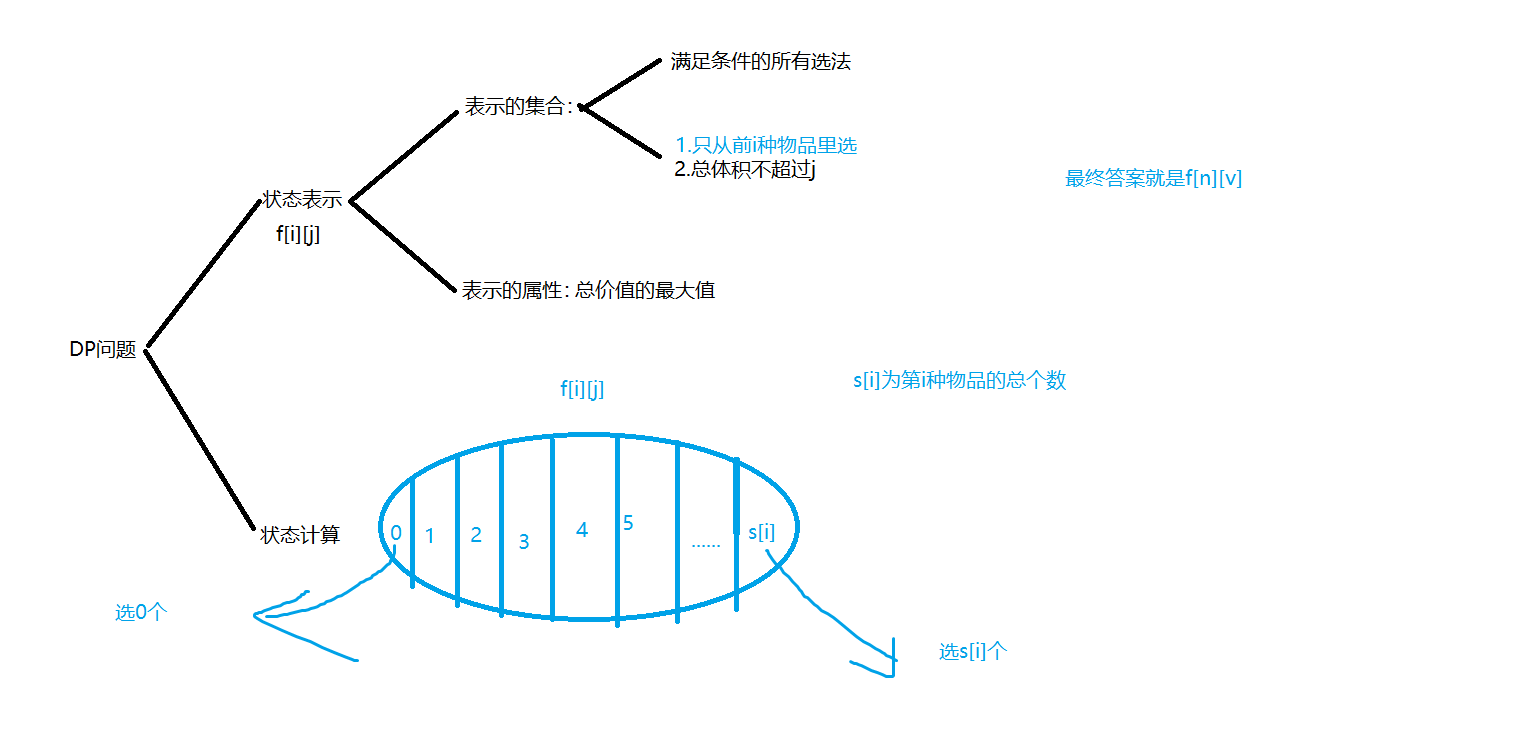
We found that this is not a simple version of the complete backpack?
Code implementation:
#include<iostream>
using namespace std;
int n,m;
const int N=110;
int v[N],w[N],s[N];//s represents the quantity of various items
int f[N][N];
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i]>>s[i];
for(int i=1;i<=n;i++){//Consider the first i items
for(int j=1;j<=m;j++){//If the volume is 0, it must be 0. It doesn't matter
for(int k=0;k<=s[i]&&k*v[i]<=j;k++){//There are at most s[i] and the volume cannot exceed
f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
}
}
}
cout<<f[n][m]<<endl;
return 0;
}
Here we can still scroll array optimization, so I won't repeat it. However, we cannot adopt the same optimization as the previous question. The reasons are as follows:

Compared with the complete knapsack, f[i][j-v] has one more item at the end, so we can't use the optimization method of the complete knapsack, but we found that we can subtract an offset and then use the sliding window to optimize, which will be in the multiple knapsack 3 (wait for my dynamic programming to be raised first, it's estimated to take a long time...)
Multiple backpack 2
Example: AcWing4
The data range of this problem is large, and the timeout is determined by the above method. Therefore, we consider optimization. We think that we can select 0~s[i] times for the i-th item. Then we use binary optimization to press multiple i-th items into one and ensure that it can be selected 0~s[i] times. Then our time complexity will become O(nvlog s), and we can pass it. For example, If 16 items can be selected for the first item, then we treat 1 item as an item, 2 items as an item, 4 items as an item, 8 items as an item, and the rest as an item. In this way, we can combine arbitrarily, that is, divide a number into the power of 2, which starts from 0 and increases continuously, If you can't divide them, the rest will be divided into one. Finally, you can get any number of combinations of the items. Next, we can directly make 01 backpack.
Code implementation:
#include<iostream>
using namespace std;
int n,m;
const int N=12010,M=2010;//Each item has a maximum of 2000 items and is divided into 11 items at most. Here, 12 items are calculated for insurance, so N is 12 * 1000
int v[N],w[N];
int f[M];
int main(){
cin>>n>>m;
int cnt=0;
for(int i=1;i<=n;i++){
int a,b,s;
cin>>a>>b>>s;
int k=1;
while(k<=s){
cnt++;
v[cnt]=a*k;
w[cnt]=b*k;
s-=k;
k*=2;
}
if(s){
cnt++;
v[cnt]=s*a;
w[cnt]=s*b;
}
}
n=cnt;
for(int i=1;i<=n;i++){//01 Backpack
for(int j=m;j>=v[i];j--){
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
cout<<f[m]<<endl;
return 0;
}
Group Backpack
Example: AcWing9
There are several groups of items in this question, and the v and w of items in each group may be different. At most one item can be selected in each group, which is similar to the previous problem.
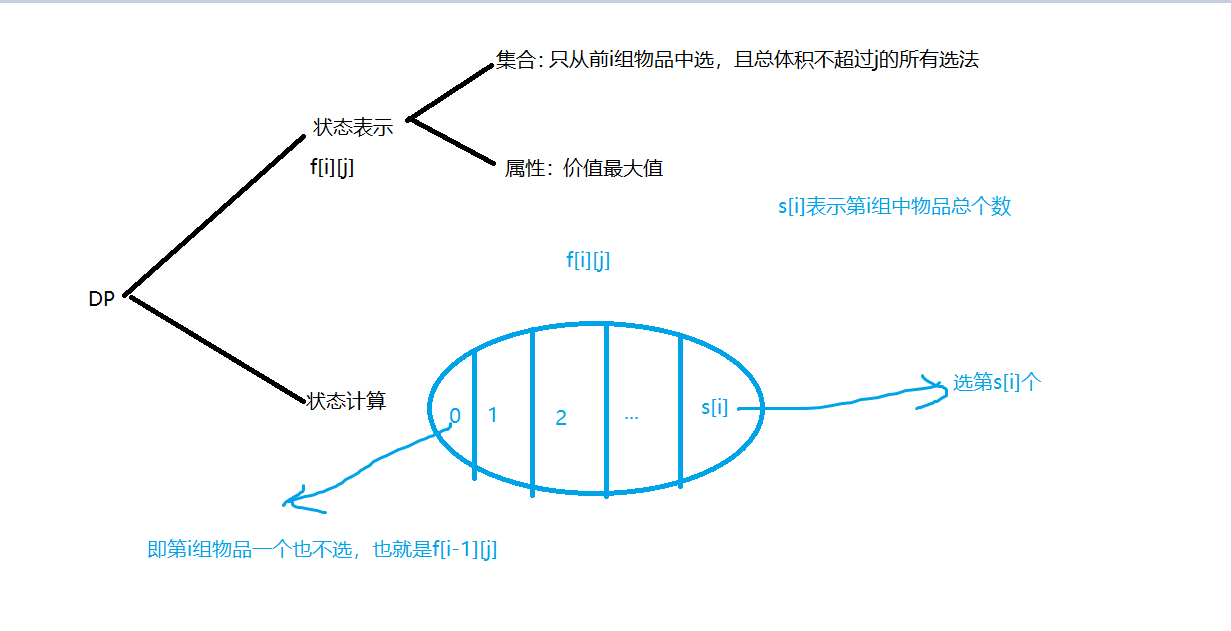
It can also be optimized into one dimension here. I'll write one dimension directly
Code implementation:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int n, m;
int v[N][N], w[N][N], s[N];
int f[N];
int main(){
cin >> n >> m;
for (int i = 1; i <= n; i ++ ){
cin >> s[i];
for (int j = 0; j < s[i]; j ++ )
cin >> v[i][j] >> w[i][j];
}
for (int i = 1; i <= n; i ++ )
for (int j = m; j >= 1; j -- )//You can't enumerate k and then J here, because the previous item has changed the front of the f array when enumerating the next item, so it can't be optimized into one dimension. However, if you only use the rolling array to optimize or don't optimize the space, you can enumerate k and j first
for (int k = 0; k < s[i]; k ++ )
if (v[i][k] <= j)
f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
cout << f[m] << endl;
return 0;
}
Linear DP
As the name suggests, linear DP mainly refers to the linearity of the state transition equation. For example, it should be easy to think about it line by line (I hope so...)
Digital triangle
A classic question. Example: AcWing898
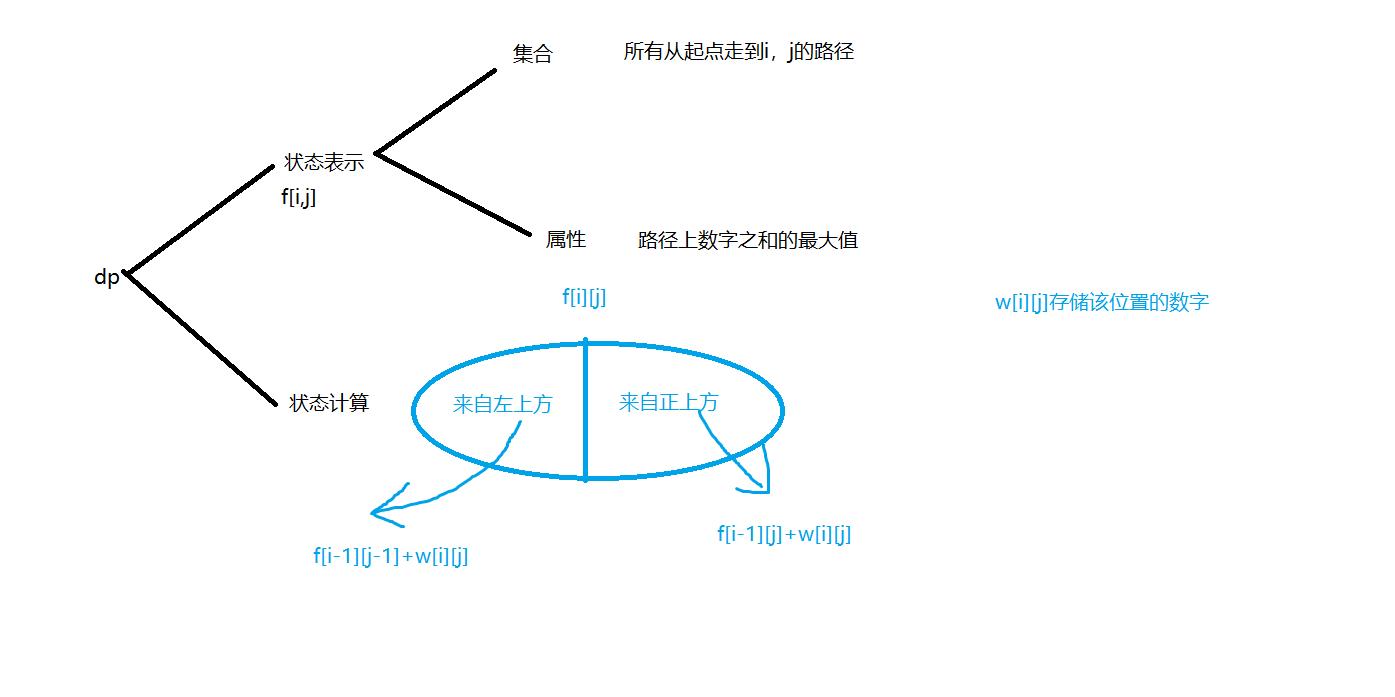
However, it should be noted that there are negative numbers in this problem, so we first initialize all the arrays to a very small value. Here is a trick, which can be initialized to a very small negative number with memset(dp,128,sizeof 128). In addition, considering that dp[1][1] is transferred from dp[0][0] and dp[0][1], these two numbers are initialized to 0.
Code implementation:
#include<iostream>
#include<cstring>
using namespace std;
int n;
const int N=510;
int a[N][N];//That is, the w array in the figure
int dp[N][N];//That is, the f array in the figure
int main(){
cin>>n;
memset(dp,128,sizeof(dp));
dp[0][1]=dp[0][0]=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){
cin>>a[i][j];
dp[i][j]=max(dp[i-1][j],dp[i-1][j-1])+a[i][j];
}
}
int res=-1e9;
for(int i=1;i<=n;i++) res=max(res,dp[n][i]);
cout<<res<<endl;
return 0;
}
Longest ascending subsequence 1
It is also a very classic question. For example: AcWing895
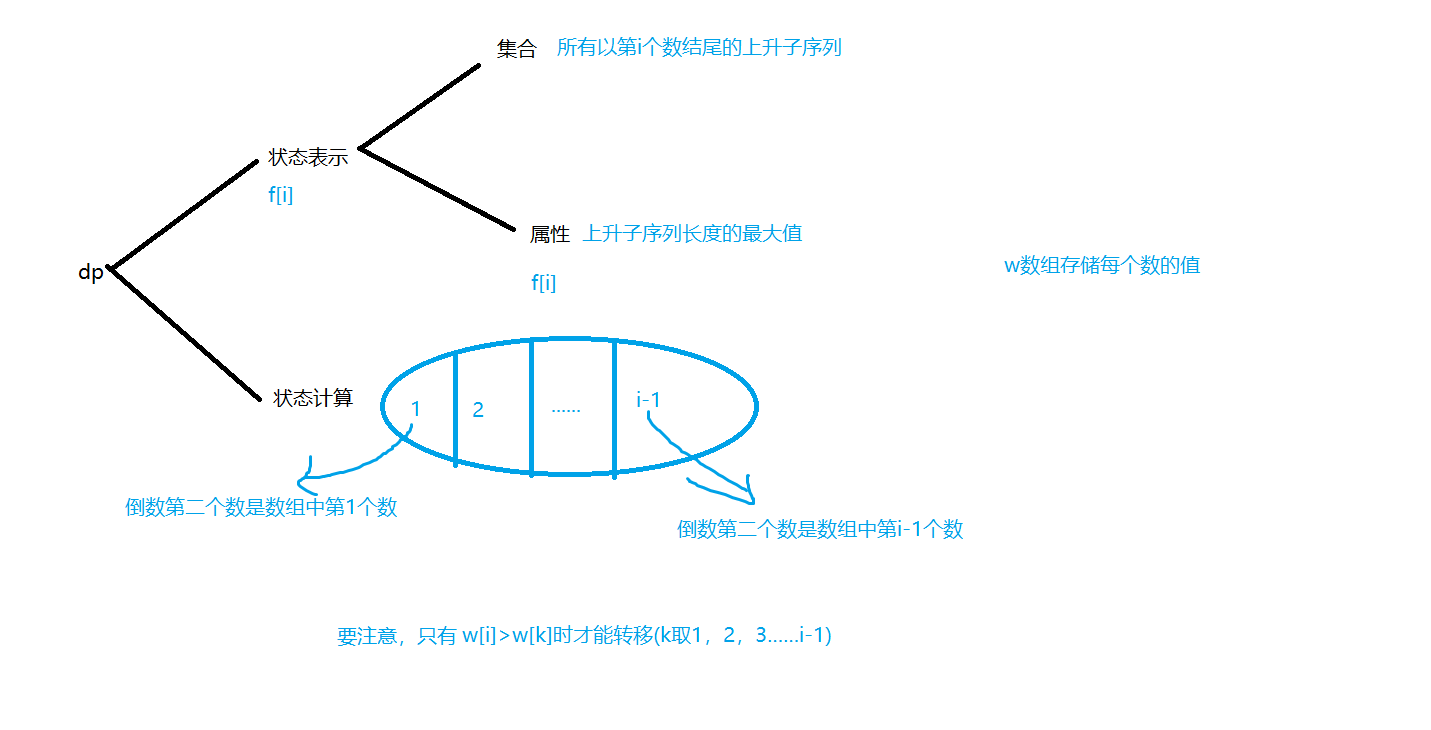
In addition, if it can be transferred, f[i] can be regarded as the rising subsequence length ending with the j-th number + 1. (J is the order of the selected numbers)
Code implementation:
#include<iostream>
using namespace std;
int n;
const int N=1e4+10;
int a[N];
int f[N];
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",a+i);
for(int i=1;i<=n;i++){
f[i]=1;//At least it is also 1, that is, there is only a[i]
for(int j=1;j<i;j++){//Enumerate the 1~i-1 number as the penultimate number
if(a[j]<a[i]){//It can only be transferred when it rises
f[i]=max(f[i],f[j]+1);
}
}
}
int res=0;//Record maximum
for(int i=1;i<=n;i++) res=max(res,f[i]);//Find the longest
printf("%d",res);
return 0;
}
If we want to record the longest sequence, we just need to open an additional array and modify the code slightly.
#include<iostream>
using namespace std;
int n;
const int N=1e4+10;
int a[N];
int f[N];
int g[N];//g[i] indicates the subscript of the previous number of the sequence ending with I
void print(int k){
if(k==0){//k is 0, indicating that the recursion is completed
return ;
}
print(g[k]);//Recursion to the last layer
printf("%d ",a[k]);//Print
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",a+i);
for(int i=1;i<=n;i++){
f[i]=1;
g[i]=0;//The sequence has only one number, and the previous number is 0
for(int j=1;j<i;j++){
if(a[j]<a[i]){
if(f[i]<f[j]+1){
f[i]=f[j]+1;
g[i]=j;//The subscript of the first number in the sequence ending with i is j
}
}
}
}
int res=1;//res record the subscript of the maximum value
for(int i=1;i<=n;i++){
if(f[i]>f[res]){
res=i;
}
}
printf("%d\n",f[res]);//Maximum output
print(res);//Recursive printing, because if we print normally, it is in reverse order, so recursive printing
return 0;
}
Longest ascending subsequence 2
Example: AcWing896
The data range of this problem is relatively large. The previous method must not work. Optimization should be considered.
We classify the ascending subsequence by the length. For each ascending subsequence of length, we only record the one with the smallest ending value (with more ascending space). Similar to a greedy thought. We can get that the value at the end of the sequence with length 6 must be greater than the value at the end of the sequence with length 5 (think about it carefully, you can use the idea of backstepping). In this way, when enumerating each a[i], we will connect it to the end of the largest less than a[i]. It can be divided into two cases. If a[i] is greater than the end value of the longest sequence, we will add a[i] to the end. Otherwise, we will find the first value greater than or equal to a[i] and change it to a[i].
Super easy code implementation:
Time complexity O(n*log n)
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
int n;
vector<int> ans;
int main(){
scanf("%d",&n);
int tmp;
scanf("%d",&tmp);
ans.push_back(tmp);//Just put one in first
for(int i=1;i<n;i++){
scanf("%d",&tmp);
if(tmp>ans.back()) ans.push_back(tmp);
else *(lower_bound(ans.begin(),ans.end(),tmp))=tmp;
}
printf("%d",ans.size());//Size is the longest length
return 0;
}
Longest common subsequence
Example: AcWing897
The set division of this problem is actually something.
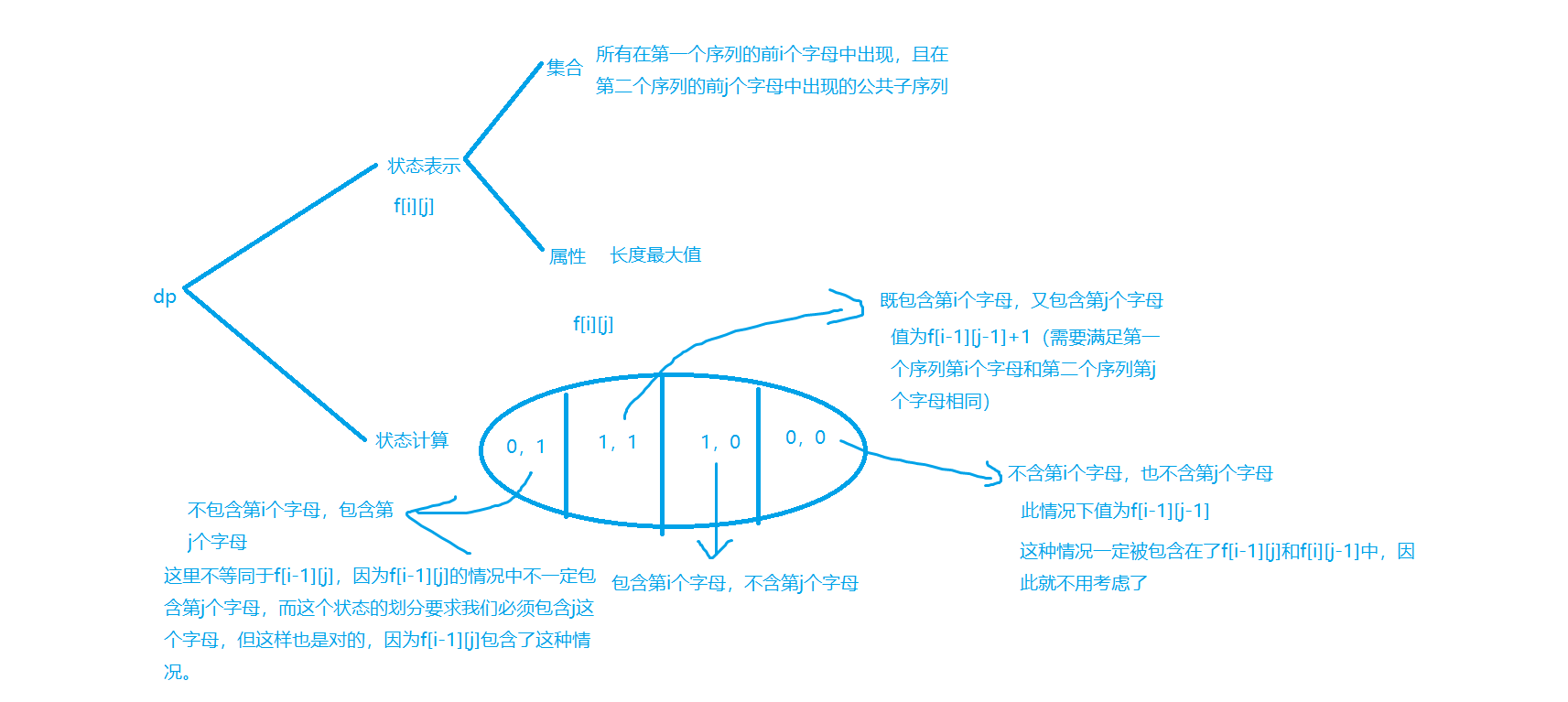
#Include < iostream > / / the code is easy
using namespace std;
const int N=1010;
int n,m;
char a[N],b[N];
int f[N][N];
int main(){
scanf("%d%d%s%s",&n,&m,a+1,b+1);
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
f[i][j]=max(f[i-1][j],f[i][j-1]);
if(a[i]==b[j]) f[i][j]=max(f[i][j],f[i-1][j-1]+1);
}
}
printf("%d",f[n][m]);
return 0;
}
Interval DP
I feel there are still templates to follow, but I'm still a vegetable and can't write
Example: AcWing282
be careful! Only two adjacent piles of stones can be merged here, so it is not the greed of Huffman tree.
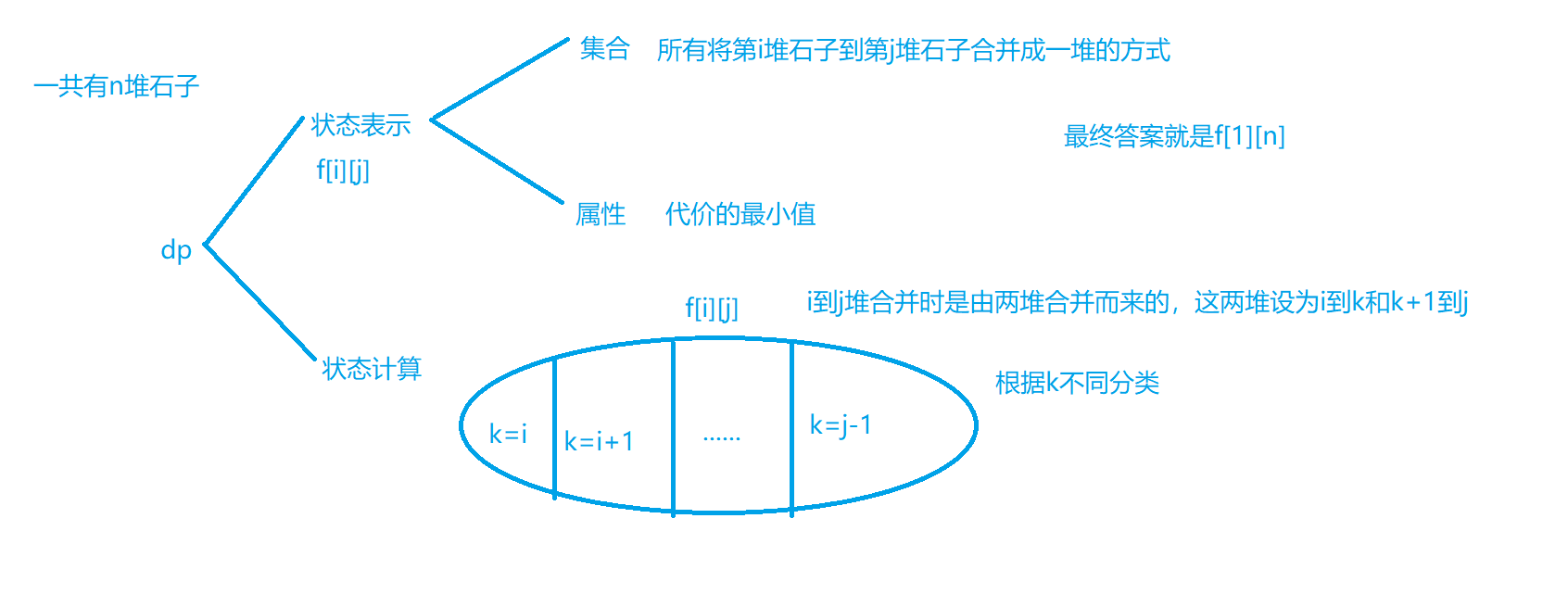
Therefore, f [i] [j] = min (the total weight of all stones from F [i] [k] + F [K + 1] [j] + I to j (calculated by prefix sum)) K can be taken as i~j-1
We first enumerate the length of the interval, then the starting point of the interval, and then the dividing point (interval dp is generally like this). We can deduce the answer according to the state transition equation. When the interval length is 1, there is no need to merge and enumeration.
Code implementation:
#include<iostream>
using namespace std;
int n;
const int N=310;
int s[N];
int dp[N][N];
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>s[i];
s[i]+=s[i-1];
}
for(int len=2;len<=n;len++){//The price of length 1 is 0, never mind
for(int i=1;i+len-1<=n;i++){//Right boundary < = n
int j=i+len-1;
dp[i][j]=1e9;//First initialize to a larger value, and then iteratively find the minimum value
for(int k=i;k<j;k++){
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+s[j]-s[i-1]);
}
}
}
cout<<dp[1][n];
return 0;
}
State compression DP
State compression dp generally includes chessboard and other types. I find it very difficult. I mainly use binary to represent the state, and then transfer the state.
Generally, when you see that the data range of the subject is very small, you can consider whether to use state compression.
chessboard
Example 1: AcWing291
A very classic question.
We are asked to count all the schemes placed. We found that as long as we put all the horizontal ones, the vertical ones can only be filled (pay attention to whether the special judgment is feasible). Therefore, we only ask for the number of legal schemes placed horizontally. In fact, it is relatively simple to judge whether it is legal. We only need to enumerate each column and judge the number of continuously empty squares in each column. If there are even bits, it is legal.
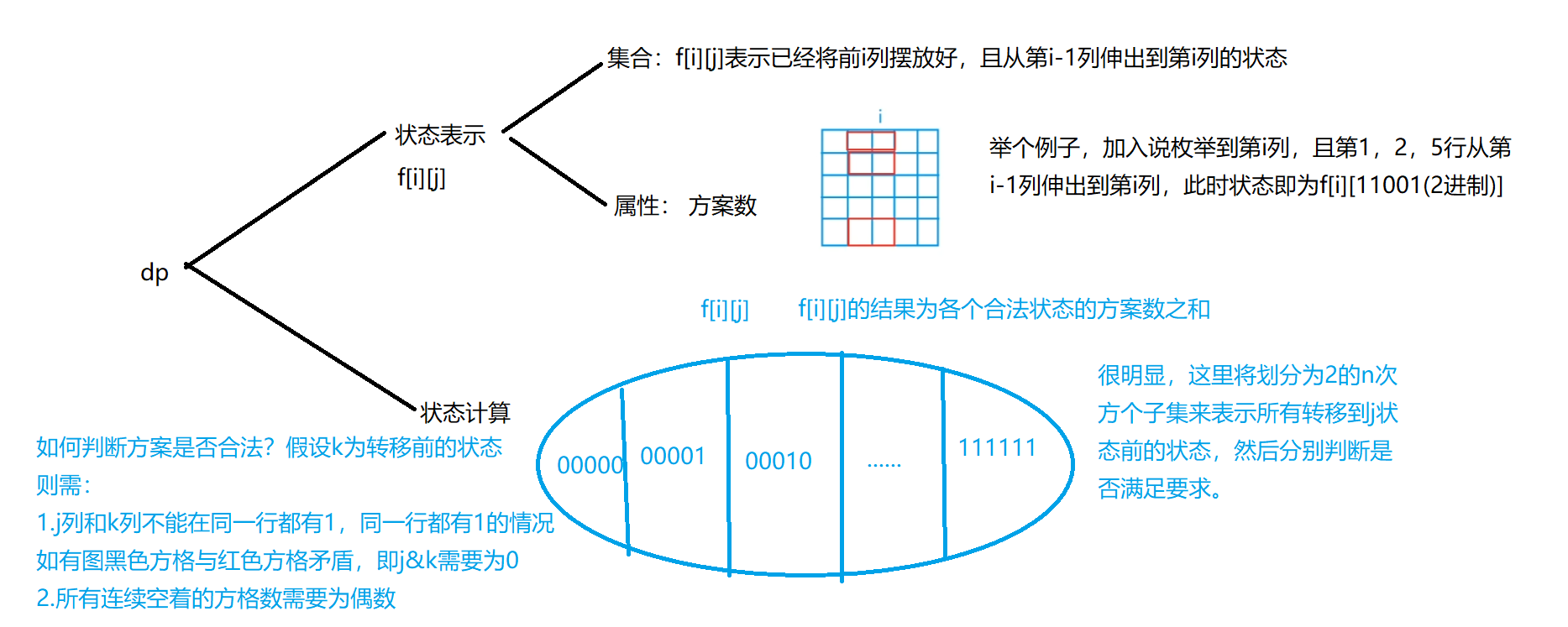
In addition, for this problem, we can also regard the process of state transition as i-1 line standing upright and being broken straight, which is also easier to understand.
In addition, the final answer to this question is f[m][0]. Suppose there are m columns in total, and the subscript starts from 0, f[m][0] means that column 0~m-1 has been arranged, and column m-1 has no square, and the number of schemes extending to column m is the number of schemes that just fill column 0~m-1. This problem can be calculated 11 * 211 * 211 times at most. Because there are multiple groups of test data, it is possible tle to optimize them without optimization. Therefore, we can preprocess them first. For each state, all the states that can be transferred to it, and then preprocess whether each state meets the continuous empty grid number is an even number, and then use these states to cycle and judge.
Code implementation:
#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
int n,m;//n is row and m is column
const int N=12,M=1<<N;//Because we have to calculate lines 0 ~ 11, N is open to 12
typedef long long LL;
LL dp[N][M];
vector<int> state[M];
bool st[M];
int main(){
while(cin>>n>>m,n|m){
int cnt;
memset(dp,0,sizeof dp);
for(int i=0;i<1<<n;i++){
st[i]=true;
cnt=0;
for(int j=0;j<n;j++){
if(i>>j&1){//If 1 is encountered
if(cnt&1){//Judge the number of the first 0
st[i]=false;//If it is an odd number, this state is unqualified
}
cnt=0;//empty
}
else cnt++;//Otherwise cnt++
}
if(cnt&1) st[i]=false;//Judge the last set of spaces (if any)
}
for(int i=0;i<1<<n;i++){//Enumerate all States of a column
state[i].clear();
for(int j=0;j<1<<n;j++){//Find the state j that can be transferred to i
if((i&j)==0&&st[i|j]){//i. j cannot have a row of horizontal pendulum at the same time, and the number of consecutive spaces must be even after j is transferred to I
state[i].push_back(j);
}
}
}
dp[0][0]=1;//Initialization, row 0 can only be placed vertically. It's a scheme. Even if there are only odd numbers in the first column, it doesn't matter. They can be transferred correctly
for(int i=1;i<=m;i++){//Calculate to column m for better output
for(int j=0;j<1<<n;j++){//Enumerate all States
for(auto k:state[j]){//Traverse the state that can be transferred to j state
dp[i][j]+=dp[i-1][k];
}
}
}
cout<<dp[m][0]<<endl;
}
return 0;
}
Collection class
Example: AcWing91
A very classic question. Commonly known as the traveling salesman problem.
Do you feel familiar with this problem? Yes, this is the last question in group A of last year's Blue Bridge Cup provincial competition (almost)!
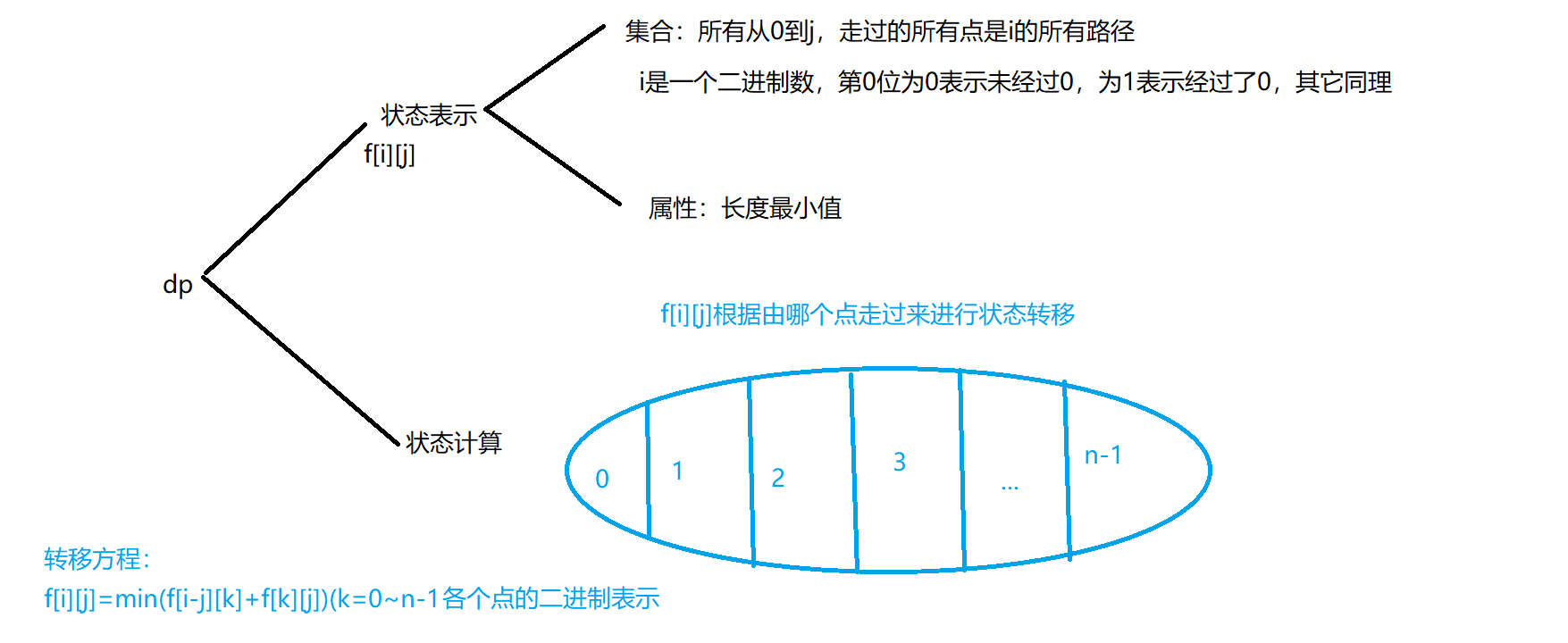
Code implementation:
#include<iostream>
#include<cstring>
using namespace std;
const int N=20,M=1<<N;
int n;
int d[N][N];
int f[M][N];
int main(){
scanf("%d",&n);
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
scanf("%d",&d[i][j]);
}
}
memset(f,0x3f,sizeof f);//Initialize to positive infinity
f[1][0]=0;//The distance from 0 to 0 and passing through 0 point (the first number from right to left is regarded as bit 0, bit 0 is 1, indicating that passing through 0 point) is 0
for(int i=0;i<1<<n;i++){//Enumerate the status of all paths
for(int j=0;j<n;j++){//Enumeration to the end of
if(i>>j&1){//Only if the state represented by i contains j
for(int k=0;k<n;k++){//Enumerate transit sites
if((i-(1<<j))>>k&1){//After i goes to point j, if k is included, it will be updated
f[i][j]=min(f[i][j],f[i-(1<<j)][k]+d[k][j]);
//If you walk through all points contained in the I state except J and the sum of the distance of the landing point at k and the distance from k to j is less than f[i][j], it will be updated
}
}
}
}
}
cout<<f[(1<<n)-1][n-1]<<endl;//The final result is the answer that goes through all points and ends in n-1
return 0;
}
Tree DP
Example: AcWing285 This question is extremely true
In fact, this problem is also a state machine model. I'll write it when I improve dynamic programming.
If we look at this question directly, we may have no clue and do not know how to express and transfer the state. In fact, we only need to discuss it by category.
We use f[i][0] to represent the maximum value of the sum of everyone's happy values in the subtree rooted by the ith person when he doesn't go to the ball
f[i][1] represents the maximum value of the sum of the happy values of all people in the subtree with him as the root when the ith person goes to the ball
Code implementation:
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 6010;
int n;
int h[N], e[N], ne[N], idx;//Chained forward star storage tree
int happy[N];//Everyone's happy value
int f[N][2];//state
bool has_fa[N];//Record whether each point has a parent node
void add(int a, int b){
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u){
f[u][1] = happy[u];
for (int i = h[u]; ~i; i = ne[i]){//~i is equal to i=- one
int j = e[i];
dfs(j);//First calculate the state of the subtree
f[u][1] += f[j][0];//If a man goes, his son cannot go
f[u][0] += max(f[j][0], f[j][1]);//Or my son won't go
}
}
int main(){
scanf("%d", &n);
for (int i = 1; i <= n; i ++ ) scanf("%d", &happy[i]);
memset(h, -1, sizeof h);
for (int i = 0; i < n - 1; i ++ ){
int a, b;
scanf("%d%d", &a, &b);
add(b, a);
has_fa[a] = true;
}
int root = 1;
while (has_fa[root]) root ++ ;//Find root node (i.e. point without parent node)
dfs(root);
printf("%d\n", max(f[root][0], f[root][1]));//The maximum value is one of the two
return 0;
}
Digital DP
Digital dp also basically has rules to follow, and the difficulty is generally no higher than that of primary school digital Olympiad (I am waste), which is basically the idea of classified discussion.
Example: AcWing338
To find the number of occurrences of each number from a to b, you can subtract the number of occurrences of each number from 1 ~a-1 by the number of occurrences of each number from 1~b. many digits dp we encounter are based on this idea.
We directly implement a function cnt(n,x) to find the number of times x appears in 0 or 1~n, and then it is easy to find it down, so the focus is the implementation of cnt function.
Drawing classification:

Code implementation:
#include<iostream>
#include<vector>
using namespace std;
int a,b;
int get(vector<int> num,int l,int r){
int res=0;
for(int i=l;i>=r;i--){
res=res*10+num[i];
}
return res;
}
int pow10(int x){
int res=1;
while(x--){
res*=10;
}
return res;
}
int cnt(int n,int x){
if(!n) return 0;//If n is 0, it returns 0 directly
vector<int> num;//num stores every bit of n
while(n){
num.push_back(n%10);
n/=10;
}
n=num.size();//Waste reuse, number of records
int res=0;
//Enumerate from the highest order
for(int i=n-1-!x;i>=0;i--){//If you count the number of 0, you can't put 0 in the highest position (set it as n-1 bit, and the lowest position is 0), because if n-1 bit is 0, in fact, the whole number has no n-1 bit
if(i<n-1){//This is not the case at the highest level
//The get function finds an integer from n-1 to i+1 digits
//pow function to find the i-th power of 10
res+=get(num,n-1,i+1)*pow10(i);
if(!x) res-=pow10(i);//If it's 0, subtract 10 to the power of i
}
if(num[i]==x){//If equal, add the number composed of all subsequent bits + 1
res+=get(num,i-1,0)+1;
}
else if(num[i]>x){//Otherwise, add 10 to the power of i
res+=pow10(i);
}
}
return res;
}
int main(){
while(cin>>a>>b,a|b){
if(a>b)swap(a,b);
for(int i=0;i<10;i++){
cout<<cnt(b,i)-cnt(a-1,i)<<" ";
}
puts("");
}
return 0;
}
In fact, it seems that it is not difficult, but it is also difficult to distinguish all the situations.
Memory search
Example: AcWing901
As soon as we look at the questions, we can think of searching, but if we search every point, we will tle. We find that we have updated the answers of other points when searching some points, so we can use this to complete the memory search.
Code implementation:
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 310;
int n, m;
int g[N][N];//g array records the answer. When - 1, it means it has not been searched
int f[N][N];
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
int dp(int x, int y){
int &v = f[x][y];
if (v != -1) return v;//Search and return directly
v = 1;//Initialize to 1
for (int i = 0; i < 4; i ++ ){//Four directions
int a = x + dx[i], b = y + dy[i];
if (a >= 1 && a <= n && b >= 1 && b <= m && g[x][y] > g[a][b])//To meet the meaning of the topic
v = max(v, dp(a, b) + 1);//to update
}
return v;
}
int main(){
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
scanf("%d", &g[i][j]);
memset(f, -1, sizeof f);
int res = 0;
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
res = max(res, dp(i, j));
printf("%d\n", res);
return 0;
}
Count class DP
Example: AcWing900
Isn't this the complete knapsack problem? Each number k in 1~n is regarded as an item occupying K volume, and each item can be used indefinitely to find all options that just reach n volume.
Strike hard:
#include <iostream>
using namespace std;
const int N = 1010, mod = 1e9 + 7;
int n;
int f[N];
int main(){
cin >> n;
f[0] = 1;
for (int i = 1; i <= n; i ++ )
for (int j = i; j <= n; j ++ )
f[j] = (f[j] + f[j - i]) % mod;
cout << f[n] << endl;
return 0;
}
DP is killing me. It's great to learn DP!