GBDT gradient lifting iterative decision tree

It is an integrated model. The base classifier adopts CART regression tree. GBDT is an algorithm to classify or regress data by using additive model and continuously reducing the residual generated in the training process.
Intuitive understanding: there is a residual between each round of prediction and the actual value. The next round will make prediction according to the residual, and finally add all predictions to get the result.
GBDT generates a weak classifier through multiple rounds of iterations, and each classifier is trained based on the residuals of the previous round of classifiers.

Intuitively understand through examples:

Assuming that the ages of the three people are 5, 6 and 7 respectively, the average age of the three people is 6, so the constant of 6 is used to predict the ages of the three people, i.e. [6, 6, 6]. The residual of each person's age = age - predicted value = [5, 6, 7] - [6, 6, 6], so the residual is [- 1, 0, 1]
Next, in order to make the model more accurate, it is necessary to reduce the residual, so establish a regression tree for the residual, and then predict the accurate residual. Assuming that the residual error of this tree is [- 0.9, 0, 0.9], sum the predicted value of the previous round with the predicted value of this round. Everyone's age = [6, 6, 6] + [- 0.9, 0, 0.9] = [5.1, 6, 6.9], which is obviously closer to the real value [5, 6, 7]. At this time, the residual error of age becomes [- 0.1, 0, 0.1], and the accuracy of prediction has been improved.

Specific ideas

Let's assume that our prediction iterates for three rounds: [5, 6, 7]

Round 1 forecast: [6, 6, 6] (average)

Round 1 residual: [- 1, 0, 1]

Round 2 prediction: [6, 6, 6] (average) + [- 0.9, 0, 0.9] (the first regression tree) = [5.1, 6, 6.9]

Round 2 residual: [- 0.1, 0, 0.1]

Round 3 prediction: [6, 6, 6] (average) + [- 0.9, 0, 0.9] (the first regression tree) + [- 0.08, 0, 0.07] (the second regression tree) = [5.02, 6, 6.97]

Residual error of the third round: [- 0.08, 0, 0.03]

The residual error is getting smaller and smaller. This prediction method is GBDT algorithm.

code implementation

1. Build test data and do simple linear regression

def create_data():
    X = []
    for i in range(100):
        x = 2 * i
        y = 3 * i
        z = i
        l = x + y + z + np.random.rand() * 10
        X.append([x,y,z,l])
    return np.array(X)
 
data = create_data()

2. Construct CART regression tree, calculate mean square error and find the best cut-off point

def calc_mse(data):
    if len(data) == 0:
        return 0
    label = data[:,-1]
    return np.var(label) * len(label)	#np.var calculation variance

def select_split(data):
    min_gini = np.inf
    best_feat = None
    best_val = None
    left = None
    right = None
    data_type = 'continuity'
    for i in range(data.shape[1]-1):
        c_set = set(data[:, i])
        for val in c_set:
            arr1,arr2 = split_data(data,i,val,data_type)
            g1 = calc_mse(arr1)		#calculation error
            g2 = calc_mse(arr2)
            # g = len(arr1) / len(data) * g1 + len(arr2) / len(data) * g2 #Gini for classification
            g = g1 + g2 # Obtain the remaining minimum mean square error
            # print(i,val,g)
            if min_gini > g:
                min_gini = g
                best_feat = i
                best_val = val
                left = arr1
                right = arr2
    return best_feat,best_val,left,right

3. Construct GBDT regression tree

def create_gbdt(dataset,n_estimators,lr):
    '''
    :param data: input data
    :param n_estimators: Number of weak classifiers
    :param lr: Learning rate, also known as residual learning rate
    :return:
    '''
    data = copy.copy(dataset)
    tree_list = []
    tree_list.append(np.mean(data[:, -1]))
    data[:, -1] = data[:, -1] - np.mean(data[:, -1])
    tree_list.append(create_tree(data))
    for i in range(1,n_estimators):
        data[:,-1] = (1 - lr) * data[:,-1] # Residual error
        tree_list.append(create_tree(data))
    return tree_list

4. Construct the prediction function and use the recursive function to construct

# Forecast single tree
def predict_one(tree,X):
    if type(tree) != dict:
        return tree
    for key in tree:
        if X[key[0]] < key[1]:
            r = tree[(key[0],key[1],'left')]
        else:
            r = tree[(key[0], key[1], 'right')]
        return predict_one(r, X)
# forecast
def predict(tree_list,X,lr):
    result = tree_list[0]
    for tree in tree_list[1:]:
        result += lr * predict_one(tree,X)
    return result

5. Test and build five trees

n_estimators = 5 
gbdt_tree = create_gbdt(data,n_estimators,0.1)
print("create gbdt:",predict(gbdt_tree,data[0,:-1]))

XGBoost decision tree algorithm based on pre sorting method

The model corresponding to XGBoost is a pile of CART trees. Continuously add trees and continuously split features to grow a tree. Adding one tree at a time is actually learning a new Han Shu f(x) to fit the residual of the last prediction. When k trees are obtained after training, the score of a sample should be predicted. In fact, according to the characteristics of the sample, each tree will fall to a corresponding leaf node, and each leaf node corresponds to a score. Finally, only the corresponding scores of each tree need to be added up to be the predicted value of the sample.

Intuitive understanding

To predict the family's preference for video games, considering that young people are more likely to like video games than old people, and men prefer video games than women, children and adults are distinguished according to age, and then men and women are distinguished by gender, and each person is graded on the preference for video games one by one, as shown in the figure below:

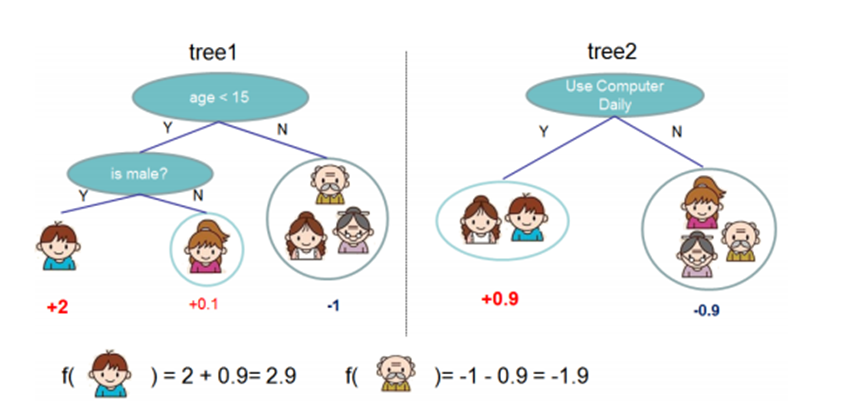
Two trees tree1 and tree2 are trained. Similar to the principle of GBDT before, the sum of the conclusions of the two trees is the final conclusion. Therefore, the child's prediction score is the sum of the scores of the nodes where the child falls in the two trees: 2 + 0.9 = 2.9 Grandpa's prediction score is the same: - 1 + (- 0.9) = - 1.9

code implementation

import xgboost as xgb
from xgboost import plot_importance
from matplotlib import pyplot as plt

# Set model parameters
params = {
    'booster': 'gbtree',
    'objective': 'multi:softmax',   
    'num_class': 3,     
    'gamma': 0.1,
    'max_depth': 2,
    'lambda': 2,
    'subsample': 0.7,
    'colsample_bytree': 0.7,
    'min_child_weight': 3,
    'silent': 1,
    'eta': 0.001,
    'seed': 1000,
    'nthread': 4,
}

plst = params.items()

dtrain = xgb.DMatrix(X_train, y_train)	#Using native xgboost library to read libsvm data
num_rounds = 200
model = xgb.train(plst, dtrain, num_rounds)

# Predict the test set
dtest = xgb.DMatrix(X_test)
y_pred = model.predict(dtest)

# Calculation accuracy
accuracy = accuracy_score(y_test, y_pred)
print ("Accuracy:", accuracy)
# Drawing feature importance
plot_importance(model)
plt.show();

result

Accuracy: 0.9166666666666666