General idea of the topic

given n ∗ m n*m The start state and target state of n * m. The state contains only three characters R, B and G. two operations are given, respectively:
1. Select one 2 ∗ 2 2*2 2 * 2, rotate the matrix clockwise 90 ° 90° 90° .
2. Select one 2 ∗ 2 2*2 For the submatrix of 2 * 2, change the matrix R into B, B into G, and G into R.
Find the minimum number of operations that can change the starting state into the target state.

Input & Output

Data range

2 ≤ n , m ≤ 4 2 \le n,m \le 4 2≤n,m≤4

thinking

The maximum number of grids in the title is 16 16 16, and each grid can be put down R , G , B R,G,B R. G, B total 3 3 3, so the total number of States is 3 16 = 43046721 3^{16}=43046721 316 = 43046721, the status can be recorded in barrels.
So we have a classic idea: starting from the starting point b f s bfs bfs search and transfer are two operations. See the minimum number of steps when reaching the target state.
But it will T L E 50 TLE 50 TLE50 .
Take another look at the topic and find that the starting state and target state are given, so we can consider two-way wide search (DBFS), that is, search from the starting point and the end point at the same time (Note: the search from the end point should be operated in the reverse direction, that is, counterclockwise and color reverse). At the same time, record the minimum steps reached by each state. If the states of the starting point and the end point coincide, You can output the answer, and the time complexity is more than twice as fast!
then T L E 90 TLE90 TLE90 .
I'm also confused...
Later, find it when transferring 2 ∗ 2 2*2 The corresponding compressed number of the matrix of 2 * 2, if the time complexity of the violent solution is O ( n ∗ m ) O(n*m) O(n * m), we have one O ( 1 ) O(1) Solution of O(1):
Suppose we are asking for coordinates ( x , y ) (x,y) (x,y), the original state is S S S. As shown in the figure:

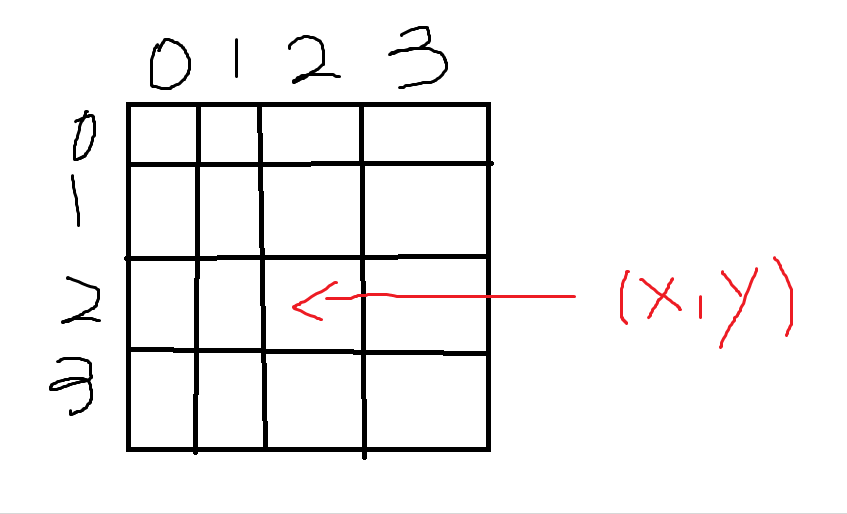
According to the order of pressure potential, we can find ( x , y ) (x,y) The bit represented by (x,y) is ( x ∗ m + y ) (x*m+y) (x * m+y) (recorded as l l l).
Then we will ( x , y ) (x,y) (x,y) move to the front, i.e S = S / 3 l S=S/3^{l} S=S/3l, last S m o d    3 S\mod 3 Smod3 is the desired color.
Ask for each grid, only need 4 4 4 times, greatly saving time and complexity, and then you can AC happily ΦωΦ.

AC code

#include<cstring>
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<map>
using namespace std;
int n,m,tot,st,en;
int a[10][10],f[1000800],p[19];
int d[10][10];
int num[10][10];
bool bz[43100400];
int to[43100400];
bool pd(int x,int y,int i,int j)
{
	if(i>=x&&j>=y&&i-x<=1&&j-y<=1)
	return 1;
	return 0;
}
int updata(int x,int y)
{
	return d[x][y]*num[x][y]+d[x+1][y]*num[x+1][y]+d[x][y+1]*num[x][y+1]+d[x+1][y+1]*num[x+1][y+1];
}
void find(int T,int x,int y)
{
	if(T==0) d[x][y]=0,d[x][y+1]=0;
	else if(T==1) d[x][y]=1,d[x][y+1]=0;
	else if(T==2) d[x][y]=2,d[x][y+1]=0;
	else if(T==3) d[x][y]=0,d[x][y+1]=1;
	else if(T==4) d[x][y]=1,d[x][y+1]=1;
	else if(T==5) d[x][y]=2,d[x][y+1]=1;
	else if(T==6) d[x][y]=0,d[x][y+1]=2;
	else if(T==7) d[x][y]=1,d[x][y+1]=2;
	else if(T==8) d[x][y]=2,d[x][y+1]=2;
	return;
}
int del(int S,int x,int y)
{
	int l=(x-1)*m+(y-1);
	int T=(S/p[l])%9;
	find(T,x,y);
	l=x*m+(y-1);
	T=(S/p[l])%9;
	find(T,x+1,y);
	return updata(x,y);
}
void chan(int x,int y,int id)
{
	if(d[x][y]==0)
	if(id==1)
	d[x][y]=1;
	else
	d[x][y]=2;
	else if(d[x][y]==1)
	if(id==1) 
	d[x][y]=2;
	else
	d[x][y]=0;
	else if(d[x][y]==2)
	if(id==1) 
	d[x][y]=0;
	else
	d[x][y]=1;
}

int change1(int S,int x,int y,int id)
{
    int de=del(S,x,y);
    int T=S-de;
    if(id==1)
    {
    	int t=d[x][y];    
		d[x][y]=d[x+1][y];
        d[x+1][y]=d[x+1][y+1];
        d[x+1][y+1]=d[x][y+1];
        d[x][y+1]=t;
	}
	else
	{
		int t=d[x][y];
		d[x][y]=d[x][y+1];
		d[x][y+1]=d[x+1][y+1];
		d[x+1][y+1]=d[x+1][y];
		d[x+1][y]=t;
	}
    T+=updata(x,y);
    return T;
}
int change2(int S,int x,int y,int id)
{
	int de=del(S,x,y);
	int T=S-de;
	chan(x,y,id),chan(x+1,y,id),chan(x,y+1,id),chan(x+1,y+1,id);
	T+=updata(x,y);
	return T;
}
int bfs()
{
	int h=0,t=1;
	f[t]=st; 
	t++;
	f[t]=en;
	bz[st]=1;
	bz[en]=0;
	to[st]=0;
	to[en]=0;
	while(h!=t)
	{
		h=(h+1)%1000000;
		int S=f[h];
		for(register int i=1;i<n;i++)
		 for(register int j=1;j<m;j++)
		 {
		 	    int T=S;
	            T=change1(T,i,j,bz[S]);
	            if(to[S]!=-1&&to[T]!=-1&&bz[S]!=bz[T])
	            return to[S]+to[T]+1;
		 	    if(to[T]==-1)
		 	    {
		 	      bz[T]=bz[S];
		 		  t=(t+1)%1000000;
		 		  f[t]=T;
		 		  to[T]=to[S]+1;
			    }		 		
			    T=change2(S,i,j,bz[S]);	 
	            if(to[S]!=-1&&to[T]!=-1&&bz[S]!=bz[T])
	            return to[S]+to[T]+1;	
			    if(to[T]==-1)
			    {
			       bz[T]=bz[S];
				   t=(t+1)%1000000;
				   f[t]=T;
				   to[T]=to[S]+1;
			    }
		 }
	}
	return -1;
}
int main()
{
	p[0]=1;
	for(int i=1;i<=16;i++)
	p[i]=p[i-1]*3;
	while(1)
	{
		scanf("%d",&n);
		if(n==0)
		return 0;
		memset(bz,0,sizeof(bz));
		memset(to,-1,sizeof(to));
		st=0,en=0;
		scanf("%d",&m);
		int lst=0;
		num[1][1]=1,lst=1;
		for(int i=1;i<=n;i++)
		 for(int j=1;j<=m;j++)
		 if(!(i==1&&j==1))
		 num[i][j]=lst*3,lst=num[i][j];
		for(register int i=1;i<=n;i++)
		 for(register int j=1;j<=m;j++)
		 {
		 	char ch=getchar();
		 	while(ch!='R'&&ch!='B'&&ch!='G')
		 	ch=getchar();
		 	if(ch=='R') st=st+num[i][j]*0;
		 	if(ch=='B') st=st+num[i][j]*1;
		 	if(ch=='G') st=st+num[i][j]*2;
		 }
		for(register int i=1;i<=n;i++)
		 for(register int j=1;j<=m;j++)
		 {
		 	char ch=getchar();
		 	while(ch!='R'&&ch!='B'&&ch!='G')
		 	ch=getchar();
		 	if(ch=='R') en=en+num[i][j]*0;
		 	if(ch=='B') en=en+num[i][j]*1;
		 	if(ch=='G') en=en+num[i][j]*2;
		 }
		printf("%d\n",bfs());
	}
}