Problem surface

There is a game in which a lattice of m rows and n columns is given on the plane. There are obstacles on some grids, and there may be English letters on grids without obstacles. Now it is required to establish a path on the empty grid, so that there is a letter at both ends of each path, and the letters at both ends are different from each other, and all letters are connected with another letter through the path. Each empty grid can be used for at most one path, and each path is one of the following six clock forms.

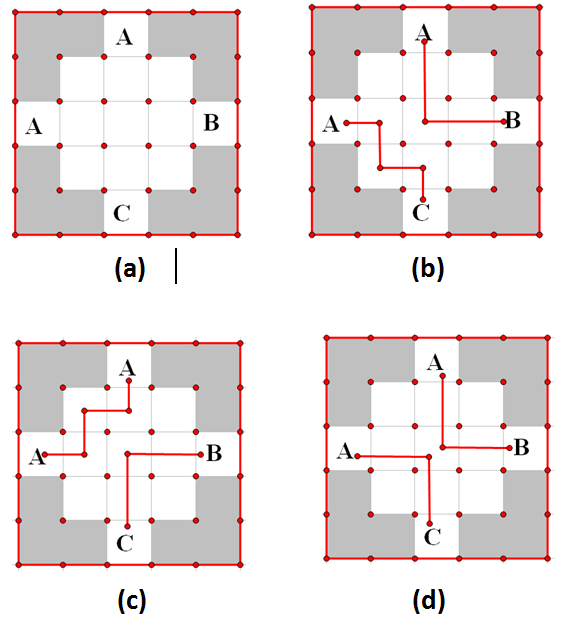
For example, in the following figure, the shaded grid represents the grid with obstacles, the white grid represents the empty grid, and the figure given at the beginning is figure (a). Figure (b) is a legal solution, which contains two paths, path AC and path AB. Figure (c) is an illegal solution because both ends of one path are the same two letters a. Graph (d) is also an illegal solution because one of the lattices is used in two paths.

Now, given an initial graph, ask at least how many grids need to establish paths to complete the above tasks.

Data range

For 30% of the data, there is at most only 4 4 Four letters, and each is different.

For 50% of the data, the letters on the plane are different.

For 100% data, T does not exceed 3 3 3， m m m and n n n not more than 16 16 16. The number of letters is positive even and no more than 8 8 8. At most two letters are the same.

Problem solution

A very good network flow problem.

find n , m ≤ 16 n,m \le 16 n. M ≤ 16, violence cannot run.
find n ∗ m n*m n * m 256 256 256, the matrix can be transformed into a graph, and the network flow solution can be considered.
First, the starting point and ending point of the point can be searched and enumerated (the total number of letters is not greater than) 8 8 8).
Because each point will only pass through once, consider splitting a point into two points. One point is responsible for inflow and one point is responsible for outflow, and then a flow is connected between the two points 1 1 1. The price is 0 0 0, which ensures that each point can be passed at most once. After dividing the start point and the end point, you can flow the source point to the flow direction s s s end flow direction t t t just run through the expense flow (note that the graph must be rebuilt every time the enumeration is completed, because the information of the graph has changed).
Both of them are forced to control the same starting point or ending point.

The idea is to convert the matrix into a graph. When there is a matrix with small data in the future, you can try to convert it into a graph and use network flow to solve the problem.

AC code

//White_gugu's code
#include<cstring>
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
struct node{
	int wz,id;
}let[20];
int head[200200],to[200200],nxt[200200],val[200200],flo[200200],sa1,sa2;
int T,n,m,cnt,nod,pop,too[22][22],fx[8]={0,0,1,-1},fy[8]={1,-1,0,0},s,t,ans1,ans2,ans=21000000;
char a[22][22];
bool bz[22],vis[20020];
int lst[200200],dep[200200],sp[200200],dl[2000100],flow[200200],num[200200];
void xx(int u,int v,int w,int s)
{
	to[cnt]=v;
	val[cnt]=w;
	flo[cnt]=s;
	nxt[cnt]=head[u];
	head[u]=cnt;
	cnt++;
}
void lian()
{	  
    memset(head,-1,sizeof(head)),cnt=0;
    for(int x=1;x<=n;x++)
	   for(int y=1;y<=m;y++)
	   {
	   	  xx(too[x][y],too[x][y]+n*m,0,1),xx(too[x][y]+n*m,too[x][y],0,0); 
	   	  if(a[x][y]=='#')
	   	  continue;
	      for(int k=0;k<4;k++)
	      {
	    	int tx=fx[k]+x,ty=fy[k]+y;
	    	if(tx>=1&&tx<=n&&ty>=1&&ty<=m&&a[tx][ty]!='#')
	    	xx(too[x][y]+n*m,too[tx][ty],(a[tx][ty]=='.'),1),xx(too[tx][ty],too[x][y]+n*m,-(a[tx][ty]=='.'),0);
		  }	   	
	   }
	for(int i=1;i<=pop;i++)
	{
		if(bz[i]==0)
		xx(s,let[i].wz,0,1),xx(let[i].wz,s,0,0);
		else
		xx(let[i].wz+n*m,t,0,1),xx(t,let[i].wz+n*m,0,0); 
	}
	return;
}
bool spfa()
{
	memset(sp,127/3,sizeof(sp));
	memset(flow,127/3,sizeof(flow));
	lst[t]=-1;
	int h=0,ti=1;
	dl[ti]=s;
	vis[s]=1;
	sp[s]=0;
	while(h<ti)
	{
		h++;
		int x=dl[h];
//		printf("%d %d\n",x,sp[x]);
		vis[x]=0;
		for(int i=head[x];i!=-1;i=nxt[i])
		{
			int y=to[i];
			if(flo[i]>0&&sp[y]>sp[x]+val[i])
			{
				sp[y]=sp[x]+val[i];
				lst[y]=x;
				num[y]=i;
				flow[y]=min(flow[x],flo[i]);
				if(!vis[y])
				ti++,dl[ti]=y,vis[y]=1;
			}
		}
	} 
	return lst[t]!=-1;
}
void wll()
{
	ans1=0,ans2=0;
	while(spfa())
	{
		ans1+=flow[t];
		ans2+=sp[t];
		int now=t;
		while(now!=s)
		{
			flo[num[now]]-=flow[t];
			flo[num[now]^1]+=flow[t];
			now=lst[now];
		}
	}
}
void dfs(int x,int y)
{
	if(y>pop/2)
	return;
	if(x==n+1)
	{
		if(y!=pop/2)
		return;
		if(bz[sa1]!=bz[sa2])
		return;
		
		lian();
		wll();
		if(ans1==pop/2)
		ans=min(ans,ans2);
		head[s]=-1,head[t]=-1;
		return;
	}
	bz[x]=1;
	dfs(x+1,y+1);
	bz[x]=0;
	dfs(x+1,y);
}
int main()
{
   scanf("%d",&T);
   while(T--)
   {
   	  ans=21000000;
   	  pop=0,nod=0,sa1=0,sa2=0;
      scanf("%d %d",&n,&m);
      s=0,t=2*n*m+1;
	  for(int i=1;i<=n;i++)
	   for(int j=1;j<=m;j++)
	   {
	      cin>>a[i][j];
	      nod++,too[i][j]=nod;
	      if(a[i][j]>='A'&&a[i][j]<='Z')
	      pop++,let[pop].wz=nod,let[pop].id=a[i][j]-'A';
	   }
	  for(int i=1;i<=pop;i++)
	   for(int j=1;j<=pop;j++)
	   if(let[i].id==let[j].id&&i!=j)
	   {
	      sa1=i,sa2=j;
	   	  break;
	   }
	   dfs(1,0);
	   if(ans==21000000)
	   printf("-1\n");
	   else
	   printf("%d\n",ans);
   }	
}