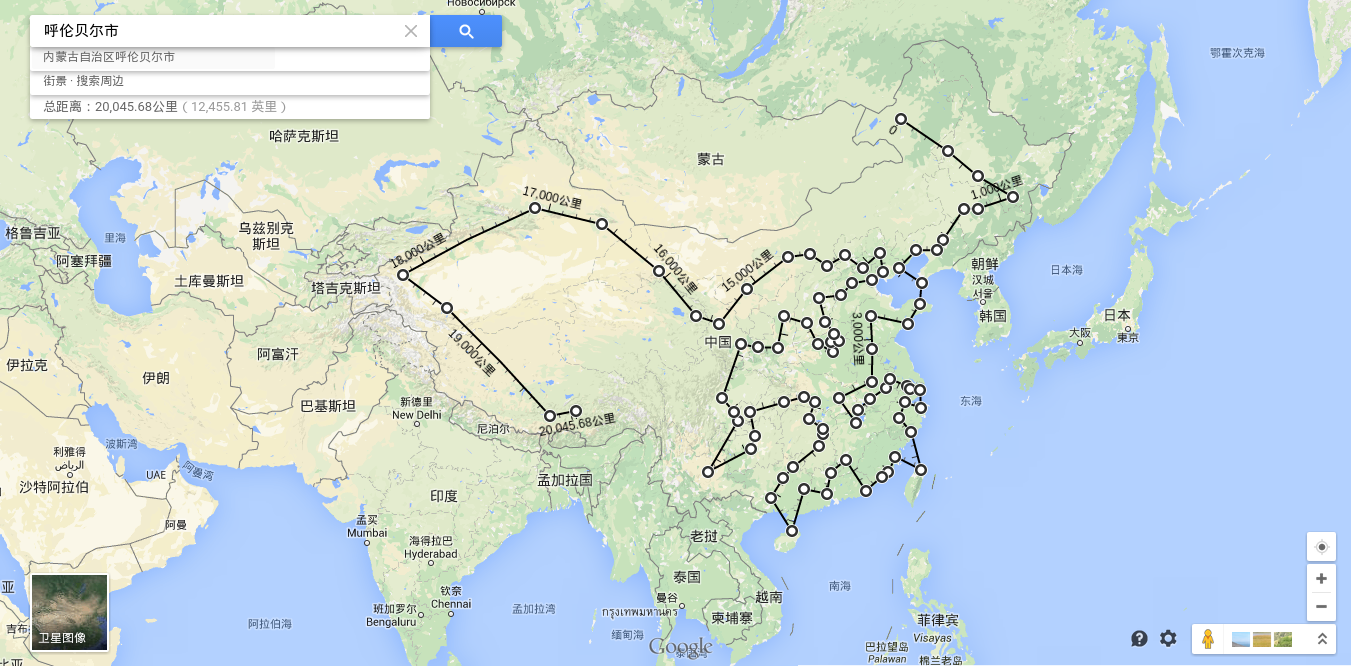
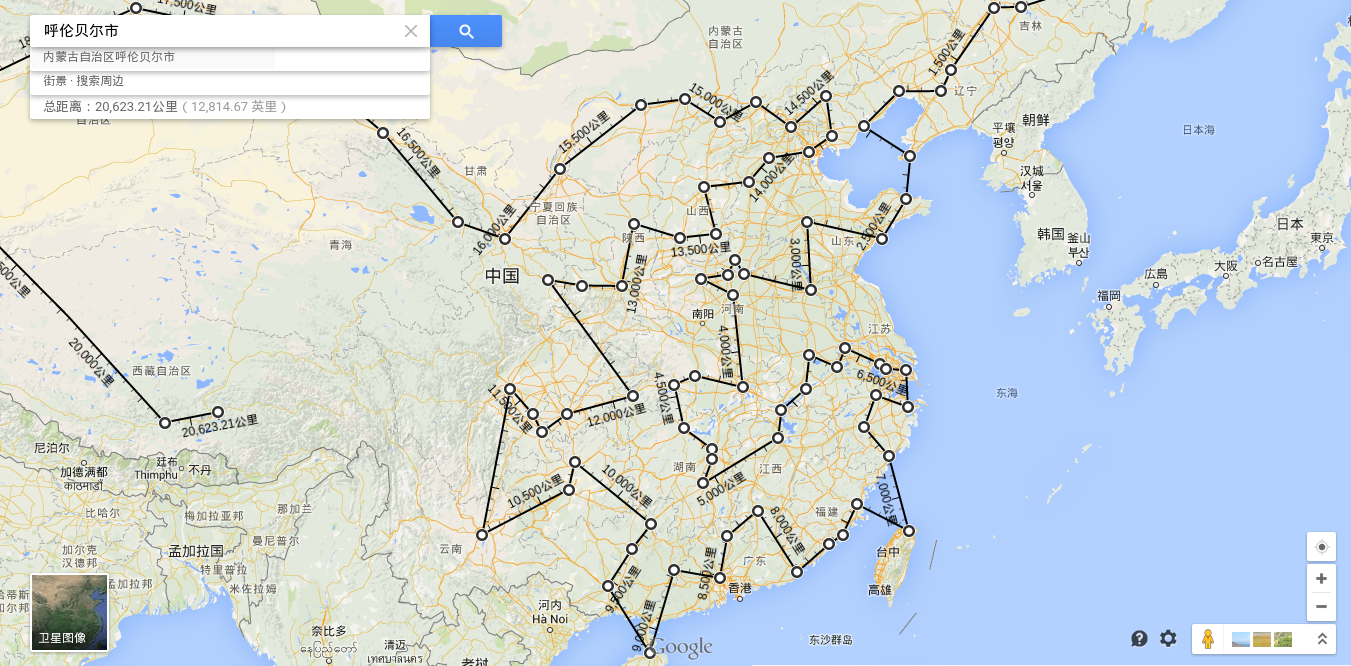
Nothing to do, I want to find a topic to practice genetic algorithm.Then it comes to the idea that genetic algorithms can be used to find the shortest path across a given city.Some Chinese cities were searched from the Internet. The distance between each city is taken as the straight line distance between them. Each city has a number, and then the arrangement of all the numbers is a solution. Each solution will get a corresponding total distance.The problem becomes one of finding the best arrangement.
A genetic algorithm is used to solve this problem. First, a random set of initial solutions is generated as the initial population.Each solution can be proliferated and varied as an individual, then the number of populations increases, and then a portion of individuals that are more satisfied with the requirements can be selected to proliferate with a higher probability through a filter function, which can evolve over generations in order to obtain the solution with the shortest total distance possible.Write the program tests and find that the results are good.
The following are explanations of some of the problems in the program.One step in the genetic algorithm is to require two individuals to cross and mutate to produce a new individual that mimics the sexual reproduction of an organism.But I really don't know how to cross the two 12345 or 31452 arrays.So the program only mutates the original permutation, but it does not cross between the two permutations.
There are many ways to mutate, here to improve the speed of the program, the mutation is divided into two exchange points and exchange between two sequences, where sequence exchange can be flipped.
In the process of running the program, it is found that the population evolves slowly. Some excellent individuals will be eliminated because of randomness, so rules to keep the best individuals are added to the program.Although this may reduce the diversity of the population and the "traversality" of the algorithm to all solutions, practice has found that a better solution can be obtained and that the optimization speed is much faster.When the optimal individual is not retained, the optimization speed will be slower, or even no further optimization, as the optimization approaches the extreme value.Maybe it's because the selection pressure is too low at this time, and perhaps a better way is to provide a variable selection pressure instead of retaining the best individual.
As for the filter function, I don't know how to do it as well as possible, so I simply choose the distance average multiplied by a factor as the filter criterion.In order to prevent the occurrence of large and small years, a second screening was carried out.
To improve the quality of the sequence, the subsequences of the sequence were optimized, and the four adjacent values were rearranged to minimize the corresponding length of the new subsequence.
For simplicity, the matrix of distances between cities and the city name needed by the program are written directly in the program, and it is easy to read from the file instead.
The code is as follows:
1 #include <iostream> 2 #include <algorithm> 3 #include <list> 4 #include <random> 5 #define NUM 37 6 7 double dis_mat[NUM][NUM] = {{0.00,101.26,543.55,624.38,270.58,408.52,421.60,618.75,457.61,855.97,1052.50,1066.24,897.04,1050.24,1341.21,1884.46,2287.62,2051.23,1522.09,1462.87,1024.61,1124.39,1206.52,1377.53,898.06,1564.50,1726.42,1248.46,362.94,1718.93,2417.35,1328.53,1185.95,917.73,2090.88,2575.17,1735.43} 8 ,{101.26,0.00,442.45,581.22,268.00,427.52,505.13,601.62,386.93,857.93,1065.92,966.74,804.46,985.11,1280.91,1816.36,2229.02,2003.83,1521.70,1444.72,926.52,1028.59,1107.84,1282.31,813.68,1474.14,1640.55,1171.72,278.25,1623.61,2502.20,1374.80,1223.32,915.77,2073.10,2608.50,1704.83} 9 ,{543.55,442.45,0.00,617.67,566.63,717.80,920.76,690.41,335.80,970.23,1199.59,550.96,468.91,821.97,1117.58,1585.54,2037.59,1874.12,1622.44,1474.56,527.26,646.97,697.39,897.52,546.73,1119.76,1311.45,920.28,301.46,1232.26,2897.35,1655.67,1480.03,1055.27,2079.11,2815.16,1665.86} 10 ,{624.38,581.22,617.67,0.00,374.61,361.57,698.60,1152.84,844.16,1425.05,1640.78,821.18,556.95,461.60,730.30,1286.82,1669.30,1426.87,1008.78,885.79,749.88,784.81,914.64,996.41,461.14,1106.84,1220.35,703.70,369.87,1314.75,2448.23,1092.94,905.93,441.65,1509.29,2201.37,1126.66} 11 ,{270.58,268.00,566.63,374.61,0.00,166.63,389.01,869.08,633.73,1119.95,1321.31,994.58,774.86,826.65,1104.36,1658.56,2043.48,1793.95,1256.65,1192.29,938.06,1014.70,1120.55,1257.41,736.12,1412.72,1552.72,1050.21,276.53,1594.22,2331.46,1125.98,966.09,650.88,1820.34,2345.77,1467.15} 12 ,{408.52,427.52,717.80,361.57,166.63,0.00,337.38,1023.15,800.08,1264.37,1457.52,1098.63,858.07,820.85,1073.64,1634.38,1992.72,1722.71,1116.61,1076.41,1035.97,1097.63,1214.46,1328.76,793.72,1459.84,1580.80,1065.20,418.00,1657.76,2190.94,959.58,799.73,516.59,1700.25,2181.53,1368.71} 13 ,{421.60,505.13,920.76,698.60,389.01,337.38,0.00,987.11,878.93,1173.66,1330.62,1382.60,1162.70,1158.18,1406.02,1967.04,2311.62,2026.95,1318.04,1332.96,1326.93,1402.90,1509.54,1643.36,1115.27,1788.37,1915.69,1401.75,656.00,1977.98,1997.27,969.74,860.07,766.65,1937.12,2235.80,1646.09} 14 ,{618.75,601.62,690.41,1152.84,869.08,1023.15,987.11,0.00,354.93,282.49,510.81,1191.46,1158.81,1483.23,1784.60,2273.73,2719.84,2534.78,2122.56,2034.63,1189.05,1316.28,1335.14,1554.70,1232.31,1792.40,1992.59,1608.16,790.12,1872.38,2905.84,1939.59,1803.11,1516.90,2661.05,3192.79,2276.35} 15 ,{457.61,386.93,335.80,844.16,633.73,800.08,878.93,354.93,0.00,636.02,865.14,856.45,804.63,1136.29,1436.51,1919.09,2367.11,2190.09,1843.57,1729.35,846.15,971.18,1002.69,1215.62,877.98,1447.06,1643.36,1253.51,474.37,1542.04,2871.80,1757.05,1599.79,1246.32,2349.41,2977.03,1951.37} 16 ,{855.97,857.93,970.23,1425.05,1119.95,1264.37,1173.66,282.49,636.02,0.00,229.38,1454.15,1437.28,1765.40,2066.86,2555.06,3002.22,2816.23,2376.46,2301.38,1457.33,1585.66,1594.98,1818.31,1513.98,2060.56,2264.18,1889.49,1067.34,2127.68,2997.08,2142.22,2019.46,1770.83,2929.28,3405.84,2551.05} 17 ,{1052.50,1065.92,1199.59,1640.78,1321.31,1457.52,1330.62,510.81,865.14,229.38,0.00,1679.15,1666.61,1991.71,2293.36,2784.24,3230.47,3040.85,2573.83,2510.29,1684.25,1812.82,1818.68,2043.19,1742.99,2286.99,2491.73,2118.66,1288.47,2348.69,3059.36,2299.04,2187.82,1970.20,3138.77,3565.77,2767.42} 18 ,{1066.24,966.74,550.96,821.18,994.58,1098.63,1382.60,1191.46,856.45,1454.15,1679.15,0.00,269.60,680.39,887.38,1201.33,1675.07,1596.81,1656.10,1438.49,75.92,160.69,146.97,364.15,401.49,610.52,821.95,603.48,730.77,685.79,3266.39,1903.85,1713.65,1218.13,1957.10,2910.99,1521.19} 19 ,{897.04,804.46,468.91,556.95,774.86,858.07,1162.70,1158.81,804.63,1437.28,1666.61,269.60,0.00,450.20,706.81,1124.68,1585.55,1454.09,1403.56,1198.82,195.21,240.44,359.60,484.87,143.27,671.19,849.75,465.45,537.44,825.11,3005.10,1634.55,1444.21,948.68,1749.11,2653.79,1316.76} 20 ,{1050.24,985.11,821.97,461.60,826.65,820.85,1158.18,1483.23,1136.29,1765.40,1991.71,680.39,450.20,0.00,301.74,834.75,1247.09,1054.07,982.01,758.10,607.41,560.72,699.48,676.50,310.79,705.30,779.80,262.02,717.61,940.04,2764.34,1335.73,1146.42,649.19,1299.62,2239.44,869.08} 21 ,{1341.21,1280.91,1117.58,730.30,1104.36,1073.64,1406.02,1784.60,1436.51,2066.86,2293.36,887.38,706.81,301.74,0.00,561.03,948.18,756.74,899.12,637.78,823.51,739.42,861.29,757.16,583.10,677.61,662.39,295.01,1017.40,924.34,2841.44,1398.80,1221.00,772.66,1073.88,2132.83,638.48} 22 ,{1884.46,1816.36,1585.54,1286.82,1658.56,1634.38,1967.04,2273.73,1919.09,2555.06,2784.24,1201.33,1124.68,834.75,561.03,0.00,474.36,508.55,1236.25,977.40,1162.31,1041.42,1110.31,910.61,1041.59,686.67,504.99,665.58,1543.36,859.33,3280.12,1857.52,1697.86,1304.10,1095.79,2327.33,764.08} 23 ,{2287.62,2229.02,2037.59,1669.30,2043.48,1992.72,2311.62,2719.84,2367.11,3002.22,3230.47,1675.07,1585.55,1247.09,948.18,474.36,0.00,357.42,1327.91,1117.50,1634.41,1514.88,1584.40,1381.40,1490.85,1147.99,947.70,1120.69,1964.64,1289.97,3366.79,2013.16,1883.41,1583.86,946.83,2201.49,805.65} 24 ,{2051.23,2003.83,1874.12,1426.87,1793.95,1722.71,2026.95,2534.78,2190.09,2816.23,3040.85,1596.81,1454.09,1054.07,756.74,508.55,357.42,0.00,972.50,773.57,1543.23,1437.89,1533.95,1362.49,1337.68,1167.34,1006.69,999.46,1754.84,1361.10,3009.60,1661.52,1538.23,1276.31,627.13,1885.96,451.91} 25 ,{1522.09,1521.70,1622.44,1008.78,1256.65,1116.61,1318.04,2122.56,1843.57,2376.46,2573.83,1656.10,1403.56,982.01,899.12,1236.25,1327.91,972.50,0.00,268.40,1581.17,1542.73,1681.23,1631.38,1261.18,1576.72,1542.06,1161.95,1372.27,1823.43,2055.13,695.37,600.88,605.98,637.04,1257.47,522.55} 26 ,{1462.87,1444.72,1474.56,885.79,1192.29,1076.41,1332.96,2034.63,1729.35,2301.38,2510.29,1438.49,1198.82,758.10,637.78,977.40,1117.50,773.57,268.40,0.00,1365.29,1314.17,1449.71,1382.61,1055.62,1314.50,1274.19,911.58,1255.48,1560.51,2304.01,900.79,766.02,568.35,628.49,1499.21,332.15} 27 ,{1024.61,926.52,527.26,749.88,938.06,1035.97,1326.93,1189.05,846.15,1457.33,1684.25,75.92,195.21,607.41,823.51,1162.31,1634.41,1543.23,1581.17,1365.29,0.00,129.01,183.56,370.68,325.57,603.53,808.13,545.36,680.23,705.69,3196.88,1829.74,1639.36,1143.00,1889.92,2835.64,1454.30} 28 ,{1124.39,1028.59,646.97,784.81,1014.70,1097.63,1402.90,1316.28,971.18,1585.66,1812.82,160.69,240.44,560.72,739.42,1041.42,1514.88,1437.89,1542.73,1314.17,129.01,0.00,140.77,254.28,328.59,476.24,679.22,449.76,770.35,595.13,3230.17,1840.28,1649.01,1146.84,1812.69,2800.15,1376.78} 29 ,{1206.52,1107.84,697.39,914.64,1120.55,1214.46,1509.54,1335.14,1002.69,1594.98,1818.68,146.97,359.60,699.48,861.29,1110.31,1584.40,1533.95,1681.23,1449.71,183.56,140.77,0.00,228.27,465.01,481.77,697.89,567.09,863.78,539.35,3362.50,1978.64,1787.46,1285.97,1934.86,2938.69,1499.76} 30 ,{1377.53,1282.31,897.52,996.41,1257.41,1328.76,1643.36,1554.70,1215.62,1818.31,2043.19,364.15,484.87,676.50,757.16,910.61,1381.40,1362.49,1631.38,1382.61,370.68,254.28,228.27,0.00,537.11,254.64,472.05,471.03,1021.15,341.40,3420.71,2006.15,1815.48,1312.74,1812.43,2881.79,1383.82} 31 ,{898.06,813.68,546.73,461.14,736.12,793.72,1115.27,1232.31,877.98,1513.98,1742.99,401.49,143.27,310.79,583.10,1041.59,1490.85,1337.68,1261.18,1055.62,325.57,328.59,465.01,537.11,0.00,676.84,828.46,376.36,536.05,864.23,2902.18,1513.90,1322.80,822.46,1610.35,2512.86,1179.67} 32 ,{1564.50,1474.14,1119.76,1106.84,1412.72,1459.84,1788.37,1792.40,1447.06,2060.56,2286.99,610.52,671.19,705.30,677.61,686.67,1147.99,1167.34,1576.72,1314.50,603.53,476.24,481.77,254.64,676.84,0.00,217.86,449.20,1202.04,247.17,3466.87,2031.26,1844.40,1353.13,1669.68,2802.95,1257.00} 33 ,{1726.42,1640.55,1311.45,1220.35,1552.72,1580.80,1915.69,1992.59,1643.36,2264.18,2491.73,821.95,849.75,779.80,662.39,504.99,947.70,1006.69,1542.06,1274.19,808.13,679.22,697.89,472.05,828.46,217.86,0.00,520.08,1363.94,354.77,3500.60,2058.04,1876.97,1405.06,1552.62,2732.91,1163.18} 34 ,{1248.46,1171.72,920.28,703.70,1050.21,1065.20,1401.75,1608.16,1253.51,1889.49,2118.66,603.48,465.45,262.02,295.01,665.58,1120.69,999.46,1161.95,911.58,545.36,449.76,567.09,471.03,376.36,449.20,520.08,0.00,894.24,690.53,3017.76,1582.46,1395.27,904.96,1367.82,2410.77,933.02} 35 ,{362.94,278.25,301.46,369.87,276.53,418.00,656.00,790.12,474.37,1067.34,1288.47,730.77,537.44,717.61,1017.40,1543.36,1964.64,1754.84,1372.27,1255.48,680.23,770.35,863.78,1021.15,536.05,1202.04,1363.94,894.24,0.00,1362.13,2605.16,1356.31,1183.16,782.44,1877.49,2533.80,1486.56} 36 ,{1718.93,1623.61,1232.26,1314.75,1594.22,1657.76,1977.98,1872.38,1542.04,2127.68,2348.69,685.79,825.11,940.04,924.34,859.33,1289.97,1361.10,1823.43,1560.51,705.69,595.13,539.35,341.40,864.23,247.17,354.77,690.53,1362.13,0.00,3704.38,2272.42,2084.47,1589.23,1894.22,3045.55,1490.66} 37 ,{2417.35,2502.20,2897.35,2448.23,2331.46,2190.94,1997.27,2905.84,2871.80,2997.08,3059.36,3266.39,3005.10,2764.34,2841.44,3280.12,3366.79,3009.60,2055.13,2304.01,3196.88,3230.17,3362.50,3420.71,2902.18,3466.87,3500.60,3017.76,2605.16,3704.38,0.00,1442.74,1624.64,2115.18,2491.22,1598.96,2571.40} 38 ,{1328.53,1374.80,1655.67,1092.94,1125.98,959.58,969.74,1939.59,1757.05,2142.22,2299.04,1903.85,1634.55,1335.73,1398.80,1857.52,2013.16,1661.52,695.37,900.79,1829.74,1840.28,1978.64,2006.15,1513.90,2031.26,2058.04,1582.46,1356.31,2272.42,1442.74,0.00,191.33,694.82,1288.98,1266.79,1209.62} 39 ,{1185.95,1223.32,1480.03,905.93,966.09,799.73,860.07,1803.11,1599.79,2019.46,2187.82,1713.65,1444.21,1146.42,1221.00,1697.86,1883.41,1538.23,600.88,766.02,1639.36,1649.01,1787.46,1815.48,1322.80,1844.40,1876.97,1395.27,1183.16,2084.47,1624.64,191.33,0.00,503.59,1228.00,1389.70,1089.40} 40 ,{917.73,915.77,1055.27,441.65,650.88,516.59,766.65,1516.90,1246.32,1770.83,1970.20,1218.13,948.68,649.19,772.66,1304.10,1583.86,1276.31,605.98,568.35,1143.00,1146.84,1285.97,1312.74,822.46,1353.13,1405.06,904.96,782.44,1589.23,2115.18,694.82,503.59,0.00,1185.74,1760.44,879.99} 41 ,{2090.88,2073.10,2079.11,1509.29,1820.34,1700.25,1937.12,2661.05,2349.41,2929.28,3138.77,1957.10,1749.11,1299.62,1073.88,1095.79,946.83,627.13,637.04,628.49,1889.92,1812.69,1934.86,1812.43,1610.35,1669.68,1552.62,1367.82,1877.49,1894.22,2491.22,1288.98,1228.00,1185.74,0.00,1259.87,436.01} 42 ,{2575.17,2608.50,2815.16,2201.37,2345.77,2181.53,2235.80,3192.79,2977.03,3405.84,3565.77,2910.99,2653.79,2239.44,2132.83,2327.33,2201.49,1885.96,1257.47,1499.21,2835.64,2800.15,2938.69,2881.79,2512.86,2802.95,2732.91,2410.77,2533.80,3045.55,1598.96,1266.79,1389.70,1760.44,1259.87,0.00,1574.69} 43 ,{1735.43,1704.83,1665.86,1126.66,1467.15,1368.71,1646.09,2276.35,1951.37,2551.05,2767.42,1521.19,1316.76,869.08,638.48,764.08,805.65,451.91,522.55,332.15,1454.30,1376.78,1499.76,1383.82,1179.67,1257.00,1163.18,933.02,1486.56,1490.66,2571.40,1209.62,1089.40,879.99,436.01,1574.69,0.00} 44 }; 45 46 unsigned int order[24][4] = { 47 {0,1,2,3},{0,1,3,2},{0,2,1,3} 48 ,{0,2,3,1},{0,3,1,2},{0,3,2,1} 49 ,{1,0,2,3},{1,0,3,2},{1,2,0,3} 50 ,{1,2,3,0},{1,3,0,2},{1,3,2,0} 51 ,{2,0,1,3},{2,0,3,1},{2,1,0,3} 52 ,{2,1,3,0},{2,3,0,1},{2,3,1,0} 53 ,{3,0,1,2},{3,0,2,1},{3,1,0,2} 54 ,{3,1,2,0},{3,2,0,1},{3,2,1,0}}; 55 //Individual, randomly generating an initial sequence 56 struct unit{ 57 unsigned int path[NUM]; 58 inline unit(){ 59 for( unsigned int i = 0; i < NUM; ++i) 60 path[i] = i; 61 std::random_shuffle(path, path+NUM); 62 } 63 inline unit(const unit & val){ 64 for( unsigned int i = 0; i < NUM; ++i) 65 path[i] = val.path[i]; 67 } 68 inline unit operator = (const unit & val){ 69 for(unsigned int i = 0; i < NUM; ++i) 70 path[i] = val.path[i]; 71 return *this; 72 } 76 inline double distance(){ 77 double dis = 0.0; 78 for(unsigned int i = 1; i < NUM; ++i) 79 dis += dis_mat[path[i-1]][path[i]]; 80 return dis; 81 } 82 }; 83 //Optimize at the left end of the sequence, returning the number corresponding to the rearrangement order 84 unsigned int shortest_path4l(unit & theone){ 85 unsigned int reti = 0; 86 double shortdis = 0.0; 87 for(unsigned int j = 0; j < 3; ++j) 88 shortdis += dis_mat[theone.path[order[0][j]]][theone.path[order[0][j+1]]]; 89 shortdis += dis_mat[theone.path[order[0][3]]][theone.path[4]]; 90 for( unsigned int i = 1; i < 24; ++i){ 91 double dis = 0.0; 92 for(unsigned int j = 0; j < 3; ++j){ 93 dis += dis_mat[theone.path[order[i][j]]][theone.path[order[i][j+1]]]; 94 } 95 dis += dis_mat[theone.path[order[i][3]]][theone.path[4]]; 96 if(dis < shortdis){ 97 shortdis = dis; 98 reti = i; 99 } 100 } 101 return reti; 102 } 103 //Optimized function corresponding to right endpoint 104 unsigned int shortest_path4r(unit & theone, unsigned int o){ 105 unsigned int reti = 0; 106 double shortdis = 0.0; 107 shortdis += dis_mat[theone.path[o-1]][theone.path[o+order[0][0]]]; 108 for( unsigned int j = 0; j < 3; ++j) 109 shortdis += dis_mat[theone.path[o+order[0][j]]][theone.path[o+order[0][j+1]]]; 110 for(unsigned int i = 1; i < 24; ++i){ 111 double dis = dis_mat[theone.path[o-1]][theone.path[o+order[i][0]]]; 112 for(unsigned int j = 0; j < 3; ++j) 113 dis += dis_mat[theone.path[o+order[i][j]]][theone.path[o+order[i][j+1]]]; 114 if(dis < shortdis){ 115 shortdis = dis; 116 reti = i; 117 } 118 } 119 return reti; 120 } 121 //Optimized functions in general 122 unsigned int shortest_path4(unit & theone, unsigned int o){ 123 unsigned int reti = 0; 124 double shortdis = dis_mat[theone.path[o-1]][theone.path[o+order[0][0]]]; 125 for(unsigned int j = 0; j < 3; ++j) 126 shortdis += dis_mat[theone.path[o+order[0][j]]][theone.path[o+order[0][j+1]]]; 127 shortdis += dis_mat[theone.path[o+order[0][3]]][theone.path[o+4]]; 128 for(unsigned int i = 1; i < 24; ++i){ 129 double dis = dis_mat[theone.path[o-1]][theone.path[o+order[i][0]]]; 130 for( unsigned int j = 0; j < 3; ++j) 131 dis += dis_mat[theone.path[o+order[i][j]]][theone.path[o+order[i][j+1]]]; 132 dis += dis_mat[theone.path[o+order[i][3]]][theone.path[o+4]]; 133 if(dis < shortdis){ 134 shortdis = dis; 135 reti = i; 136 } 137 } 138 return reti; 139 } 140 //Reorder Subsequences 141 void ch_order( unit & theone, unsigned int o, unsigned int i){ 142 unsigned int ach[4]; 143 for(unsigned int j = 0; j < 4; ++j) 144 ach[j] = theone.path[o+order[i][j]]; 145 for(unsigned int j = 0; j < 4; ++j) 146 theone.path[o+j] = ach[j]; 147 } 148 //Optimize function, call the above four functions, to optimize the entire sequence 149 void optimize(unit & theone){ 150 ch_order(theone, 0, shortest_path4l(theone)); 151 for( unsigned int i = 1; i < NUM - 5; ++i) 152 ch_order(theone, i, shortest_path4(theone, i)); 153 ch_order(theone, NUM-4, shortest_path4r(theone,NUM-4)); 154 } 155 156 std::random_device rd; 157 std::mt19937 mt(rd()); 158 std::bernoulli_distribution witera(0.5); //Whether to iterate 159 std::bernoulli_distribution wch(0.5); //Is Variation 160 std::bernoulli_distribution porl(0.5);//Selection point or sequence variation 161 std::bernoulli_distribution wrev(0.5);//Is it flipped 162 std::uniform_int_distribution<> startpoint(0, NUM-1);//Start or end of point or sequence variation 163 //Variogram, choosing the direction of variation with a certain probability 164 unit ch_unit( const unit & theone){ 165 unit ret(theone); 166 if(wch(mt)){ 167 if(porl(mt)){ 168 auto start1 = startpoint(mt); 169 auto start2 = startpoint(mt); 170 if( start1 != start2){ 171 auto temp = ret.path[start1]; 172 ret.path[start1] = ret.path[start2]; 173 ret.path[start2] = temp; 174 } 175 } 176 else {//Selective Sequence Variation 177 decltype(startpoint(mt)) cutpoint[4]; 178 do{//Select where the two variant sequences begin and end 179 for(unsigned int i1 = 0; i1 < 4; ++i1) 180 cutpoint[i1] = startpoint(mt); 181 for(unsigned int i1 = 0; i1 < 3; ++i1) 182 for( unsigned int i2 = i1+1; i2 < 4; ++i2) 183 if(cutpoint[i1] > cutpoint[i2]) 184 std::swap(cutpoint[i1], cutpoint[i2]); 185 } 186 while(cutpoint[1] == cutpoint[2]); 188 unsigned int tmp[NUM]; 189 unsigned int pos = 0; 190 for(unsigned int i3 = 0; i3 < cutpoint[0]; ++i3) 191 tmp[pos++] = ret.path[i3]; 192 if(wrev(mt)){ 193 for(unsigned int i3 = cutpoint[3]; i3 >= cutpoint[2]; --i3) 194 tmp[pos++] = ret.path[i3]; 195 } 196 else{ 197 for(unsigned int i3 = cutpoint[2]; i3 <= cutpoint[3]; ++i3) 198 tmp[pos++] = ret.path[i3]; 199 } 200 for(unsigned int i3 = cutpoint[1]+1; i3 < cutpoint[2]; ++i3) 201 tmp[pos++] = ret.path[i3]; 202 if(wrev(mt)){ 203 for(int i3 = cutpoint[1]; i3 >= cutpoint[0]; --i3) 204 tmp[pos++] = ret.path[i3]; 205 } 206 else{ 207 for(unsigned int i3 = cutpoint[0]; i3 <= cutpoint[1]; ++i3) 208 tmp[pos++] = ret.path[i3]; 209 } 210 for(unsigned int i3 = cutpoint[3]+1; i3 < NUM; ++i3) 211 tmp[pos++] = ret.path[i3]; 212 for(unsigned int i3 = 0; i3 < NUM; ++i3) 213 ret.path[i3] = tmp[i3]; 214 } 215 } 216 if(witera(mt)) 217 return ch_unit(ret); 218 else 219 return ret; 220 } 221 //Proliferative function 222 void add_unit( std::list<unit> & conti){ 223 const unsigned int SIZE = conti.size(); 224 unsigned int i = 0; 225 auto itr = conti.begin(); 227 while(i < SIZE){ 228 conti.push_back(ch_unit(*itr)); 229 ++itr; 230 ++i; 232 } 233 } 234 //The multiplication factor used in the filter function satisfies the normal distribution, so that good or bad individuals have a certain probability of being selected and eliminated, in order to increase randomness, traversal and reduce the possibility of obtaining local minimum values 235 std::normal_distribution<double> normald(1., 0.25); 236 237 void select(std::list<unit> & conti ) 238 auto thekeep = *(conti.begin());//Keep the Optimal Individual 239 for(auto itk = conti.begin(); itk != conti.end(); ++itk) 240 if(thekeep.distance() > itk->distance()) 241 thekeep = *itk; 242 double av_dis = 0.0; 243 auto SIZE = conti.size(); 244 for(auto itr = conti.begin(); itr != conti.end(); ++itr) 245 av_dis += itr->distance(); 246 av_dis /= conti.size(); 247 std::list<unit> tmp_conti; 248 auto itr = conti.begin(); 249 while(itr != conti.end()){ 250 if(normald(mt) * itr->distance() > av_dis*2000./SIZE){ 251 tmp_conti.push_back(*itr); 252 itr = conti.erase(itr); 253 } 254 else{ 255 ++itr; 256 } 257 } 258 conti.push_back(thekeep); 259 unsigned int looplimit = 0; 260 while(conti.size() < 2000*0.5){//Secondary screening to avoid large-and-small-year phenomenon 261 auto back_num = 2000 - conti.size(); 262 auto itb = tmp_conti.begin(); 263 auto TMPSIZE = tmp_conti.size(); 264 while(itb != tmp_conti.end()){ 265 if(normald(mt) * itb->distance() < av_dis*back_num/TMPSIZE){ 266 conti.push_back(*itb); 267 itb = tmp_conti.erase(itb); 268 } 269 else{ 270 ++itb; 271 } 272 } 273 if(++looplimit < 10) 274 break; 275 } 276 } 277 278 void print_city(unsigned int order[NUM]){ 279 std::vector<std::string> cityname = { 280 "Beijing","Tianjin", "Qingdao", "Zhengzhou", "Shijiazhuang","Taiyuan","Hohhot","Shenyang", "Dalian", "Changchun", "Harbin","Shanghai","Nanjing","Wuhan", "Changsha", "Guangzhou", "Haikou", "Nanning", "Chengdu", "Chongqing", "Suzhou", "Hangzhou", "Ningbo","Wenzhou", "Hefei", "Fuzhou", "Xiamen", "Nanchang", "Jinan", "Taipei", "Urumchi","Xining", "Lanzhou", "Xi'an", "Kunming", "Lhasa", "Guiyang"}; 281 for(unsigned int i = 0; i < NUM; ++i) 282 std::cout << cityname[order[i]] << std::endl; 283 } 284 285 int main(){ 286 std::list<unit> conti; 287 for( unsigned int i = 0; i < 10000; ++i){ 288 conti.push_back(unit()); 289 } 290 // std::cout << "biaozhi 1" << std::endl; 291 //Algebra of reproduction 292 for(unsigned int i = 0; i < 100000; ++i){ 293 add_unit(conti); 294 std::cout << "Population Number:" << conti.size() << std::endl; 295 for(auto itr = conti.begin(); itr != conti.end(); ++itr) 296 optimize(*itr); 297 select(conti); 298 auto itr = conti.begin(); 299 auto dis = itr->distance(); 300 while(itr != conti.end()){ 301 if(dis > itr->distance()) 302 dis = itr->distance(); 303 ++itr; 304 } 305 std::cout << "distance = " << dis << std::endl; 306 } 307 auto itr = conti.begin(); 308 auto dis = itr->distance(); 309 auto theone = *itr; 310 while(itr != conti.end()){ 311 if(dis > itr->distance()){ 312 dis = itr->distance(); 313 theone = *itr; 314 } 315 ++itr; 316 } 317 std::cout << "short distance " << dis << std::endl; 318 print_city(theone.path); 319 return 0; 320 }
The resulting path looks good as shown in the diagram.
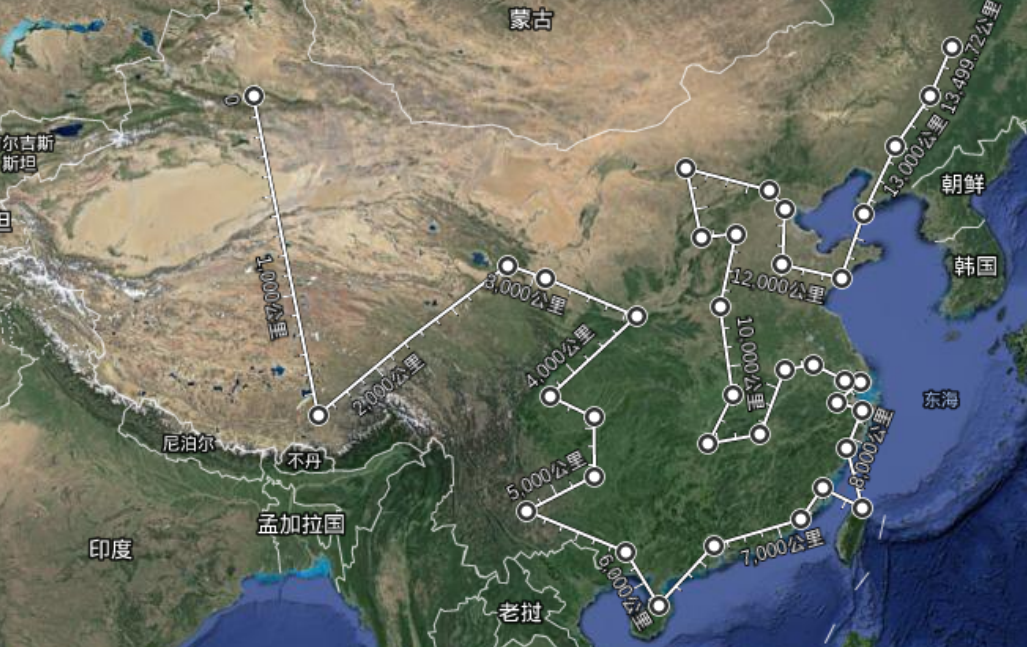
Later, 88 cities were used, and the resulting routes were as follows: better routes obtained by keeping the best individual and better routes obtained by not keeping the best individual: