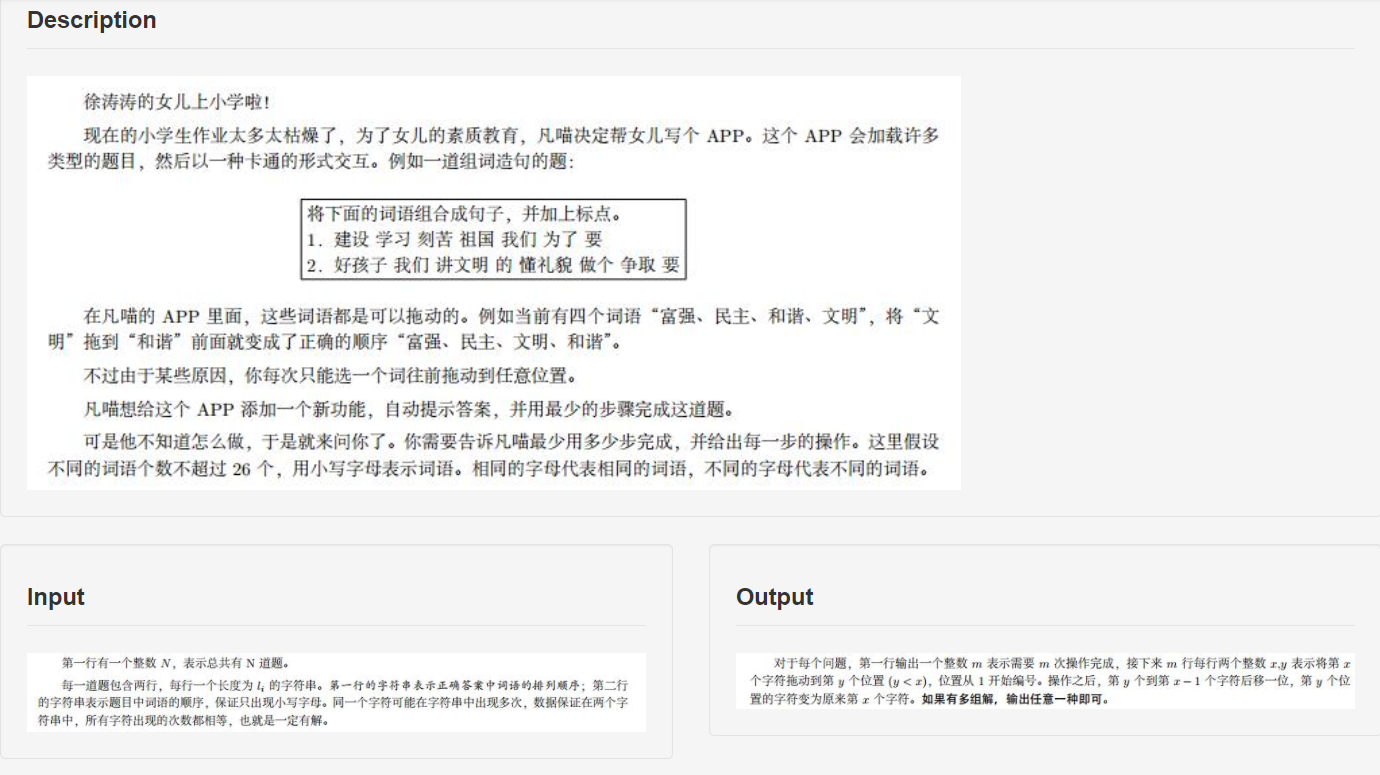
Idea:
First of all, it is easy to think that each character must be moved only once, which is the best.
Then, the most important thing is that if we move the b string (target string) to match the bits from the back of the a string, we don't need to disturb the matched bits, so we can think of reversing dp.

Let f[i][j] mean that the a string i~n is matched, and the b string uses j~n (some may not move, some may be pulled out)

Consider how to transfer:

1. f[j][k]=f[j+1][k+1], that is to say, the current position a[i]=b[j] can not be moved. The above situation does not need to be pulled out (no contribution + 1), so update the status first, otherwise there will be problems

2. f[i][j]=f[i+1][j], that is to say, I can be filled out. Then judge whether the number of characters of b string (j+1 ~ n) is larger than that of a string (i+1 ~ n).

3. f[i][j]=f[i][j+1] means that b[j+1] will give up legal matching, but match with a position in a previous a where legal matching cannot be carried out. However, this transfer must be conditional. You can't give up if you want to give up. The premise is that there is a position in a that can make an illegal match with it

We also require mobile solutions.

First find the points that don't move:
Record which state each state is pushed from. If f[i][j] is pushed from f[i + 1] [j+1], it is obvious that Bj and Ai will not move.

Then we directly simulate it again, from the left to the right of string A (target string). For each Ai, if it is moved, we can directly find any one in string B that has not been moved and needs to be moved. Here, we can directly move string B to the right, which is O anyway( n 2 n^2 n2)

#include <cstdio>
#include <iostream>
#include <cstring>

using namespace std;

const int N = 2e3 + 10;
char s[N], t[N];
int m, n, bz[N], bz2[N], sum1[30][N], sum2[30][N], f[N][N], g[N][N][2], len;

int main()
{
	freopen("chinese.in", "r", stdin);
	freopen("chinese.out", "w", stdout);
	scanf("%d", &m);
	while(m--)
	{
		memset(g, 0, sizeof(g));
		memset(bz, 0, sizeof(bz)),memset(bz2, 0, sizeof(bz2));
		memset(sum1, 0, sizeof(sum1)), memset(sum2, 0, sizeof(sum2));
		memset(f, 127 / 3, sizeof(f));
		scanf("%s%s", s + 1, t + 1);
		n = strlen(s + 1);
		for(int i = n; i >= 1; i--)
		{
			for(int j = 0; j <= 25; j++)
				sum1[j][i] = sum1[j][i + 1], sum2[j][i] = sum2[j][i + 1];
			sum1[s[i] - 'a'][i]++; sum2[t[i] - 'a'][i]++;	
		}
		for(int i = 1; i <= n + 1; i++)
		{
			f[n + 1][i] = n - i + 1, 
			g[n + 1][i][0] = n + 1, g[n + 1][i][1] = i + 1;
		}
		for(int i = n; i >= 1; i--)
		{
			for(int j = i; j >= 1; j--)
			{	
				if(sum2[s[i] - 'a'][j] >= sum1[s[i] - 'a'][i] && f[i][j] > f[i + 1][j])
				{
					f[i][j] = f[i + 1][j];
					g[i][j][0] = i + 1, g[i][j][1] = j;
				}
				if(s[i] == t[j] && f[i + 1][j + 1] < f[i][j])
                    f[i][j] = f[i + 1][j + 1], g[i][j][0] = i + 1, g[i][j][1] = j + 1;
                if(f[i][j + 1] + 1 < f[i][j])
                    f[i][j] = f[i][j + 1] + 1, g[i][j][0] = i, g[i][j][1] = j + 1;
			}
		} 
		printf("%d\n", f[1][1]);
		int x = 1, y = 1;
		while(x <= n && y <= n)
		{
			int xx = g[x][y][0], yy = g[x][y][1];
            if(x + 1 == xx && y + 1 == yy)
                bz[x] = 1, bz2[y] = 1;
            x = xx; y = yy;
		}
		for(int i = 1; i <= n; i++)
		 if(!bz[i]) 
		 {
            for(int j = i; j <= n; j++)
			 if(!bz2[j] && s[i] == t[j])
			 {
                for(int k = j; k >= i + 1; k--)
                    bz2[k] = bz2[k - 1], t[k] = t[k - 1];
                printf("%d %d\n", j, i);
                break;
             }
        }
	}
	return 0;
}