Full code: https://github.com/abmcar/ACM/tree/master/OpenjudgeNow/Codeforces/Good%20Bye%202021-2022%20is%20NEAR

Better reading experience: http://www.abmcar.top/archives/goodbye20212022isneara-d-ti-jie

A. Integer Diversity

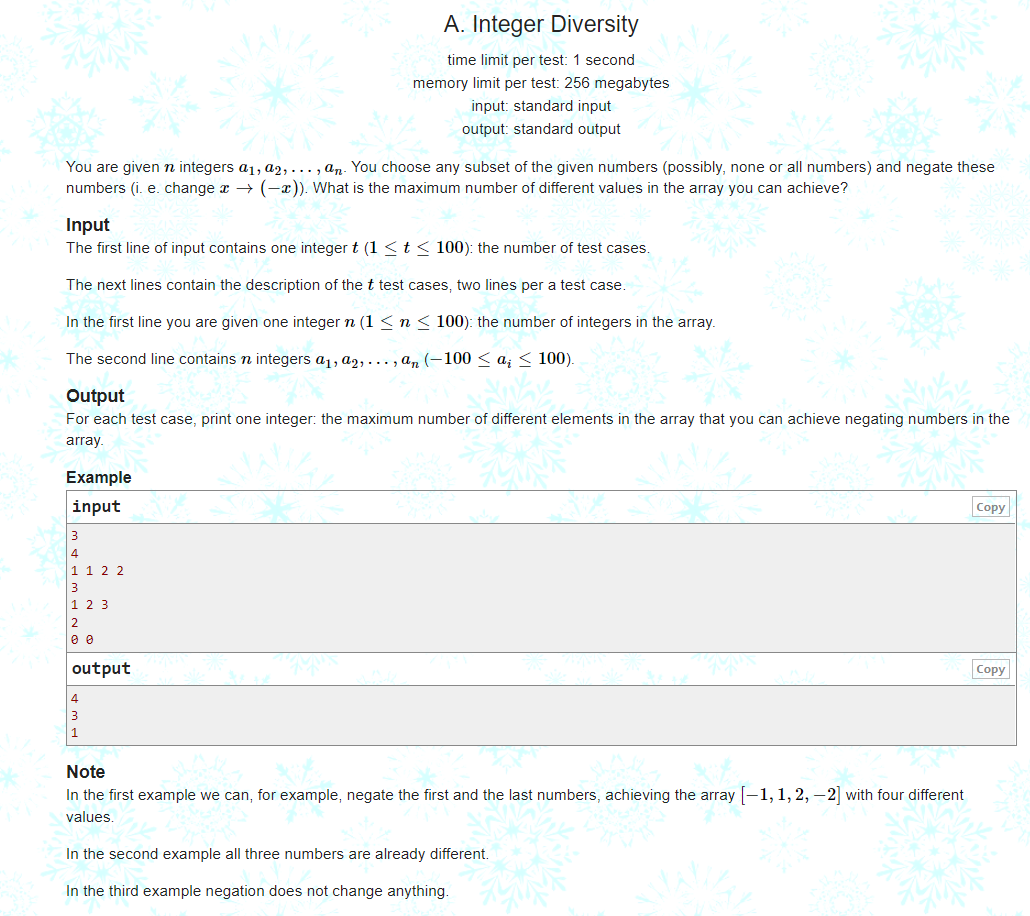
Give you n numbers, you can choose any number to multiply by - 1, and ask how many different numbers you can get at most
Idea: use map to record the number of occurrences of each number and traverse the map. If a number occurs more than twice and it is multiplied by - 1, the answer is + 2, otherwise the answer is + 1
Pit point: pay attention to skip it Second = = 0

void work()
{
    cin >> n;
    map<int,int> M;
    int ans = 0;
    for (int i = 1; i <= n; i++)
    {
        int temp;
        cin >> temp;
        M[temp]++;
    }
    for (auto it : M)
    {
        // cout << it.first << " " << it.second << endl;
        // if (it.second == 0)
        //     continue;
        if (it.second >= 2 && M[it.first * -1] == 0)
            ans += 2;
        else
            ans++;
    }
    cout << ans << endl;
}

B. Mirror in the String

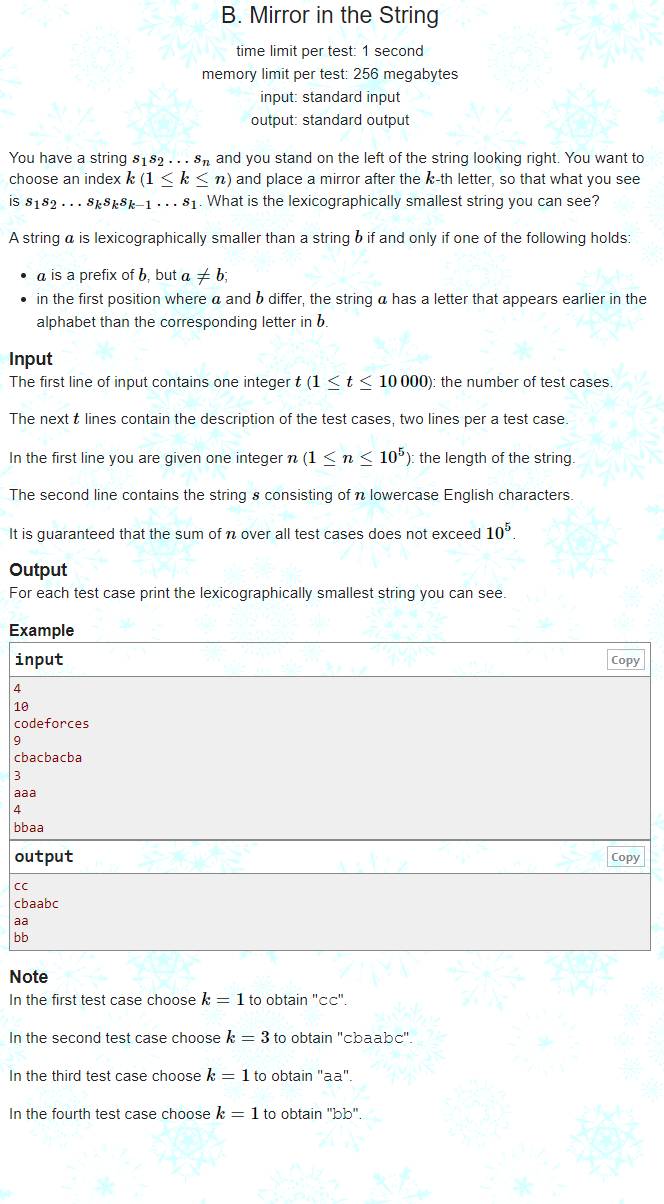
Give you a string s1s2s3s4... sn, you can choose a k to form a new string t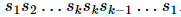, the dictionary order is small t
Idea: the newly constructed string we sent is a palindrome string and requires the smallest dictionary order. Imagine how much k should be taken if the first character of s is a?
In fact, the s1-sk we are looking for must be in descending order, otherwise the dictionary order is not optimal
Pit point: try to calculate the answers of baa and bba, and find that it needs to be judged that the initials are equal
code:

void work()
{
    string nowS;
    cin >> n >> nowS;
    int cnt = n - 1;
    for (int i = 0; i + 1 < n; i++)
        if (nowS[i] < nowS[i + 1] || (i == 0 && nowS[i] == nowS[i + 1]))
        {
            cnt = i;
            break;
        }
    string ans = nowS;
    ans = ans.substr(0, cnt + 1);
    reverse(ans.begin(), ans.end());
    ans = nowS.substr(0, cnt + 1) + ans;
    cout << ans << endl;
}

C. Representative Edges

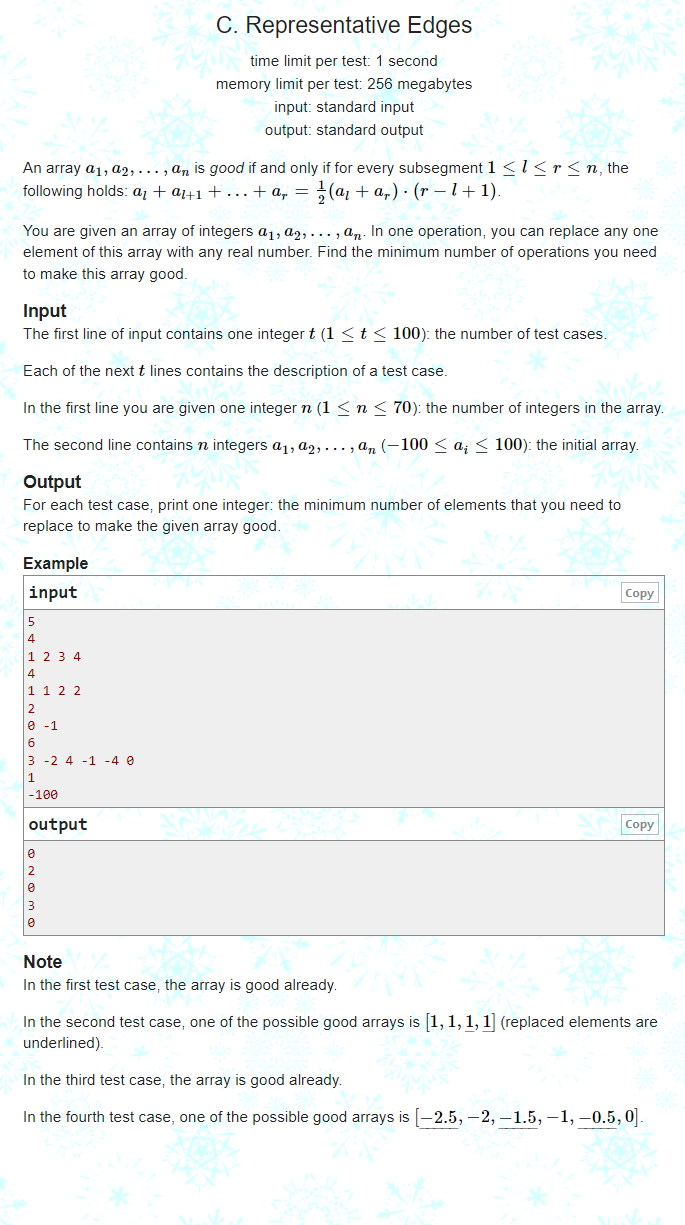
Main idea of the topic: if the array satisfies any 1 ≤ l ≤ r ≤ n, and al+al+1 +... + ar=12(al+ar) ⋅ (r − l+1), the array is called a good array. Now I give you an array arr, you can modify any number, and ask the minimum number to make it a good number group

Idea: we found that the good array for the problem is the arithmetic sequence. If an array arithmetic sequence, it must be a good array. You can enumerate all possible tolerances and record the number of corresponding numbers of each tolerance to get the minimum answer

Pit: remember that the statistical tolerance is 0

code:

void work()
{
    cin >> n;
    map<int, int> M;
    vector<int> V(n + 1);
    for (int i = 1; i <= n; i++)
        cin >> V[i], M[V[i]]++;
    int cnt = 1e9;
    for (int i = 1; i <= n; i++)
        for (int j = i + 1; j <= n; j++)
        {
            double nowD = (V[j] - V[i]) * 1.0 / (j - i);
            int nowAns = n;
            for (int k = 1; k <= n; k++)
            {
                if (abs(V[k] - (V[i] + nowD * (k - i))) < 1e-2)
                    nowAns--;
                // cout << V[k] << " " << V[i]+nowD*(k-i) << " " << nowD << " " << nowAns << endl;
            }
            cnt = min(cnt, nowAns);
        }
    for (int i = 1; i <= n; i++)
        cnt = min(cnt,n-M[V[i]]);
    cout << cnt << endl;
}

D. Keep the Average High

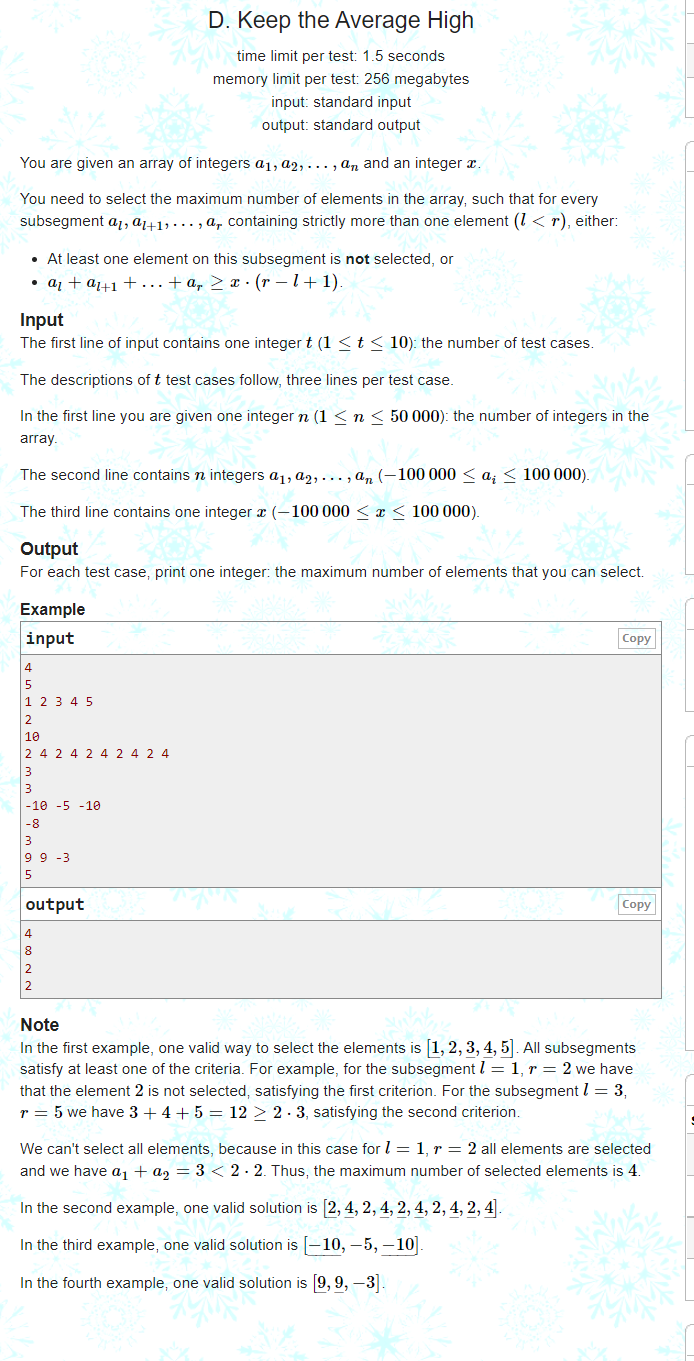
Give you an array A and a number x, let you select ans elements, so that it is satisfied for any continuous sub segment with length greater than or equal to 2
One of the elements is not selected
Sub segment and > = x * sub segment length
Find the maximum x
Idea:
For each continuous sub segment with length greater than or equal to 2, either one element is not selected, or its average number is greater than x
It can be seen that if the inter cells are satisfied, the large interval must be satisfied, so we can only judge the sub segments with length < = 3
Use dp[0][i] to represent the number selected from 0-i. at this time, the ith number is not selected
Use dp[1][i] to represent the number selected from 0-i. at this time, the ith number is selected
Use dp[2][i] to represent the number selected from 0-i. at this time, I and i-1 are selected
dp[3][i] is used to represent the number selected from 0-i. at this time, I, i-1 and i-2 are selected
It can be seen that dp[0][i] can be obtained from dp[0-3][i-1], and dp[1][i] = dp[0][i-1] + 1 (because the sub segment length required by the topic is greater than if a [i] + a [I-1] > = 2 * x)
Then dp[2][i] = max(dp[0][i - 2] + 2, dp[1][i - 1] + 1). Similarly, the transfer equation satisfied by the sub segment with length 3 can be constructed. It is not listed here, which is too difficult to write
code:

void work()
{
    for (int i = 0; i <= 3; i++)
        dp[i].clear();
    cin >> n;
    vector<int> V(n + 1);
    for (int i = 1; i <= n; i++)
        cin >> V[i];
    cin >> x;
    for (int i = 1; i <= n; i++)
    {
        dp[0][i] = max(dp[0][i - 1], dp[1][i - 1]);
        dp[0][i] = max(dp[0][i], dp[2][i - 1]);
        dp[0][i] = max(dp[0][i], dp[3][i - 1]);
        dp[1][i] = dp[0][i - 1] + 1;
        if (i >= 2 && V[i] + V[i - 1] >= 2 * x)
            dp[2][i] = max(dp[0][i - 2] + 2, dp[1][i - 1] + 1);
        if (i >= 3 && (V[i] + V[i - 1] >= 2 * x) && (V[i - 1] + V[i - 2] >= 2 * x) && (V[i - 2] + V[i - 1] + V[i] >= 3 * x))
        {
            dp[3][i] = max(dp[2][i - 1] + 1, dp[1][i - 2] + 2);
            dp[3][i] = max(dp[3][i], dp[0][i - 3] + 3);
            dp[3][i] = max(dp[3][i], dp[3][i - 1] + 1);
        }
    }
    int ans = 0;
    ans = max(dp[0][n], dp[1][n]);
    ans = max(ans, dp[2][n]);
    ans = max(ans, dp[3][n]);
    cout << ans << endl;
}