Path: a sequence of vertices consisting of contiguous edges

Path length: the sum of the number / weight of edges or arcs on the path

Loop (loop): the first vertex and the last vertex are the same path

Simple path: a path with different vertices except that the start and end points of the path can be the same

Simple loop (simple loop): a path with different vertices except that the start and end points of the path are the same

Connected graph: any two vertices in an undirected graph have paths

Strongly connected graph: any two vertices in a directed graph have paths

Minimal connected subgraph: This subgraph is a connected subgraph of G. delete any edge in this subgraph and the subgraph is no longer connected

Spanning tree: a minimal connected subgraph containing all vertices of undirected graph G

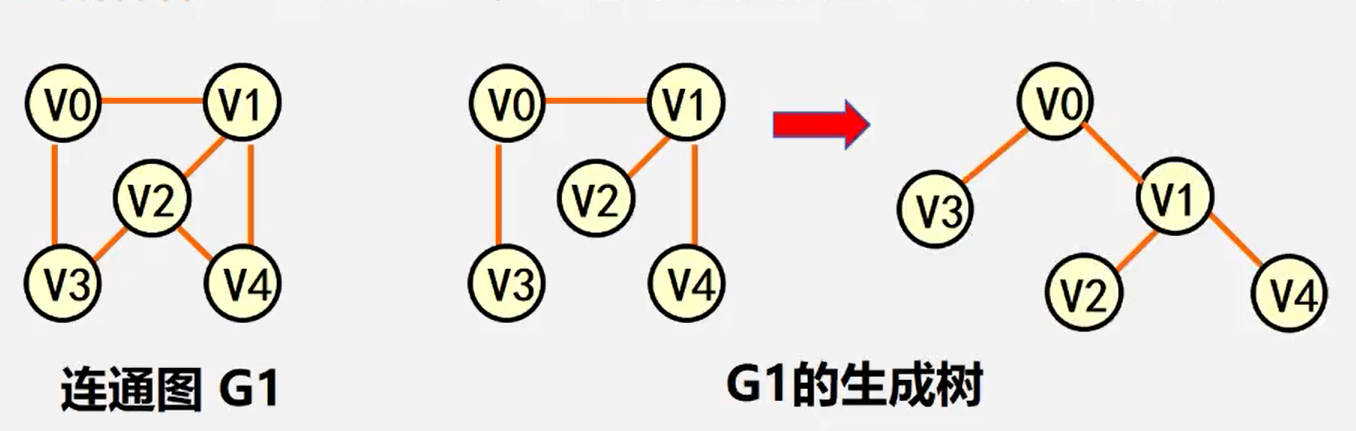
Spanning forest: for a non connected graph, a set of spanning trees composed of each connected component

Type definition of drawing:

  Storage structure of the diagram:

Logical structure of graph: many to many

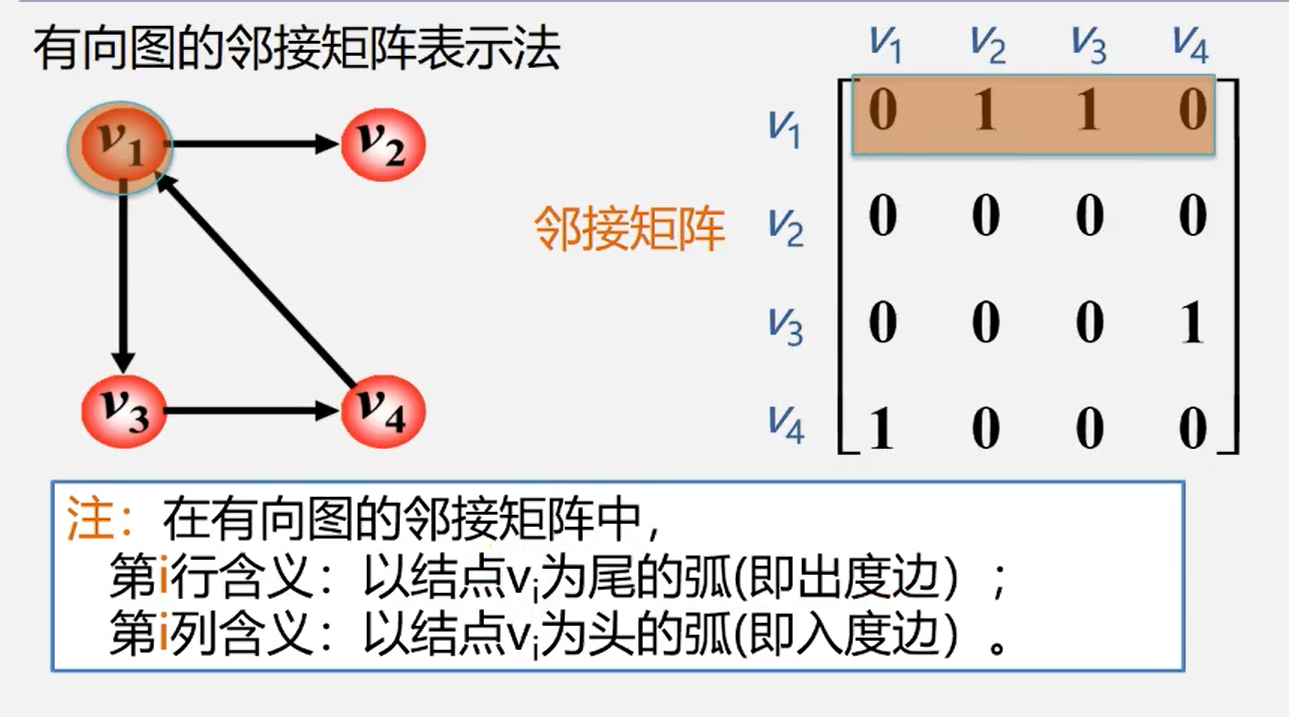
Array representation (adjacency matrix)

  The adjacency matrix of an undirected graph is symmetric

#define MVNum 100 / / maximum number of vertices
typedef char VerTexType;//Set the data type of vertices to character type
typedef int ArcType;//Assume that the weight type of the edge is integer

typedef struct
{
VerTexType vexs[MVNum];//Vertex table
ArcType arcs[MVNum][MVNum];//adjacency matrix 
int vexnum ,arcnum;//Current number of points and edges of a graph

}AMGraph;

The adjacency matrix is used to represent the undirected network:

Algorithm idea:

1. Enter the total number of fixed points and the total number of edges
2. The information of one input point is stored in the vertex table
3. Initialize the adjacency matrix so that each weight is initialized to a maximum value
4. Construct adjacency matrix

Status CreateUDN(AMGraph &G)
{
cin>>G.vexnum>>G.arcnum;//Enter the total number of vertices. Total number of sides
for(i=0;i<G.vexnum;++i)
cin>>G.vexs[i];//Enter the information of the points in turn
for(i=0;i<G.vexnum;++i)//Initialize adjacency matrix
 for(j=0;j<G.vexnum;++j)
    G.arcs[i][j] = MaxInt//The weights of the edges are set to the maximum
for(k=0;k<G.arcnum;++k)
{//Construct adjacency matrix
cin>>v1>>v2>>w;//Enter the vertex to which an edge is attached and the weight of the edge
i=LocateVex(G,v1) ;
j=LocateVex(G,v2) ;//Exactly where v1 and v2 are in G
G.arcs[i][j]=w;//Set the weight of the edge to w
G.arcs[j][i]=G.arcs[i][j]//Set the same weights for symmetrical edges
}
return OK;
}

int LocateVex(AMGraph G,VertexType u)
{//Find vertex u in Figure G, if it exists, return the subscript in the vertex table, otherwise return - 1
int i;
for(i=0;i<G.vexnum;i++)
   if(u==G.vexs[i] return i;
return -1;

}

  Advantages of adjacency matrix storage:

• Intuitive, simple and easy to understand
• It is convenient to check whether there are edges between any pair of vertices
• It is convenient to find all "critical points" of any vertex
• It is convenient to calculate the "degree" of any vertex

Disadvantages:

• Inconvenient to add and delete

• Waste of space - store sparse graphs with a large number of invalid elements

• Waste of time -- count the total number of edges in a sparse graph

Adjacency table storage graph

• Vertex: stores vertex data in a one-dimensional array in numbered order
• Edges associated with the same vertex (arc with vertex as tail): stored in a linear linked list  

Undirected graph:

characteristic:

• Adjacency table is not unique
• If an undirected graph has n vertices and e edges, its adjacency table needs n head nodes and 2e cousin points. It is suitable for storing sparse graphs  
• The degree of the vertex in the undirected graph is the number of nodes in the ith single training table

Directed graph:

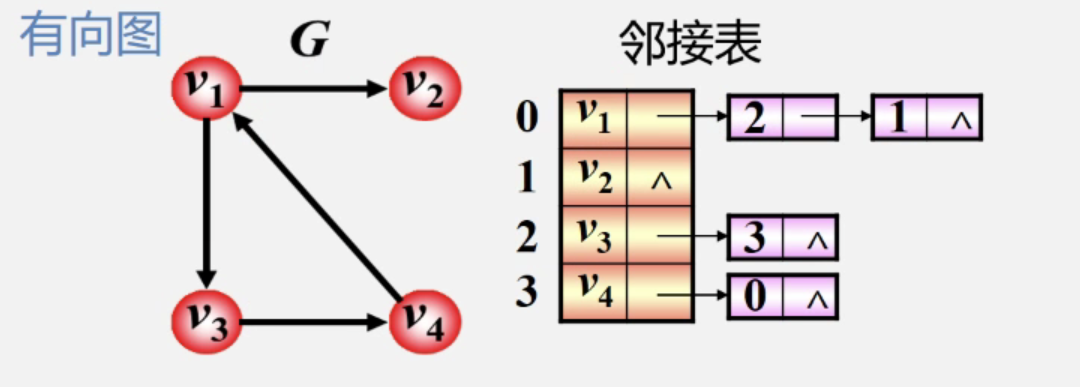  characteristic:

• The output of vertex I is the number of nodes in the i-th song solo table
• The penetration of vertex i is the number of nodes with the value of adjacent point field i-1 in the whole single training table

  Adjacency table:

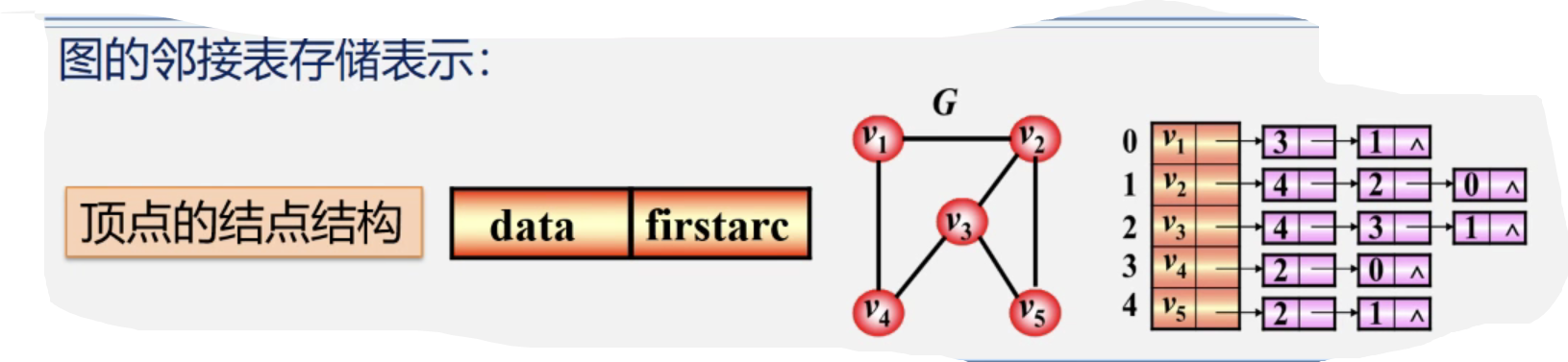
typedef struct VNode
{
VerTexType data; // Vertex information
ArcNde *firstarc; //Pointer to the first edge attached to the vertex
}VNode，AdjList[MVNum];//AdjList represents the adjacency table type

Storage representation of adjacency table of graph:

#define MVNum 100 / / maximum number of vertices
typedef struct ArcNode
{
int adjvex; //The position of the vertex that the edge points to
struct ArcNode *nextarc; // Pointer to the next edge
OtherInfo info; //Edge related information
}ArcNode;

Create an undirected network using adjacency table representation:

Algorithm idea:

• Enter the total number of vertices and edges
• Establish a vertex table. Input the information of points in turn and store it in the vertex table to initialize the pointer field of each header node to NULL
• Create an adjacency table. Enter the two vertices attached to each edge in turn, but the sequence numbers i and j of those two vertices, establish an edge node, and insert this edge node into the heads of the two edge linked lists corresponding to Vi and Vj respectively

Status CreateUDG(ALGraph &G)//Using adjacency table representation, undirected graph G is created
{
cin>>G.vexnum>>G.arcnum;//Enter the total number of vertices and edges
for(i=0;i<G.vexnum;++i))
{
cin>>G.vertices[i].data;//Enter vertex value
G.vertices[i].firstarc=NULL;//Initializes the pointer field of the header node
}//for
for(k=0;k<G.arcnum;++k)
{//Enter each edge to construct an adjacency table
cin>>v1>>v2;//Enter the two vertices to which an edge is attached
i=LocateVex(G,v1);
j=LocateVex(G,v2);
p1=new ArcNode;//Generate a new boundary point
p1->adjvex=j;//Critical point serial number is j
=1->nextarc=G.vertices[i].firstarc;
G.vertices[i].firstarc=p1;//Insert the new node p1 into the edge table header of vertex vi
p2=new ArcNode;//Generate another symmetrical new edge node p2
p2->adjvex=i;//The temporary contact number is i
p2->nextarc=G.vertices[j].firstarc;
G.vertices[j].firstarc=p2;//Insert the new node p2 into the edge table header of vertex vj
}
return OK;
}

  Adjacency table features:

• It is convenient to find all adjacent points of any vertex
• Save the space of sparse graph: N header pointers + 2E nodes (at least 2 fields per node)

Relationship between adjacency matrix and adjacency table representation:

difference:

• For any definite undirected graph, the adjacency matrix is unique (the row and column number is consistent with the vertex number), but the adjacency table is not unique (the link order is independent of the vertex number)
• The spatial complexity of adjacency matrix is the square of N, and the spatial complexity of two adjacency table is n+e

Purpose:

  Adjacency matrix is mostly used in dense graphs, while adjacency table is mostly used in sparse graphs

Cross linked list - for directed graphs:

Cross linked list is another linked storage structure of directed graph. We can also call it a linked list formed by combining the adjacency list and inverse adjacency list of directed graph

Each arc in a directed graph corresponds to an arc node in the cross linked list. At the same time, each vertex in a directed graph corresponds to a node in the cross linked list, which is called a vertex node

Traversal of graph:

Traversal definition:

Starting from a given vertex in a connected graph, visiting all the vertices in the graph along some, and making each vertex visited only once, is called graph traversal, which is the basic operation of the graph

How to avoid repeated access:

• Set the auxiliary array to mark each accessed vertex
• The initial state is 0
• When accessed, it becomes 1 to prevent multiple accesses

Depth first traversal (DFS):

method:

• After accessing a starting vertex v in the graph, V starts to access its   Any critical vertex w1

• Starting from w1, access the vertex w2 adjacent to w1 but not yet accessed

• Then start from w2 and make a similar visit

• This continues until all adjacent stores have been visited

• Then, step back to the vertex that has just been visited before to see if there are other adjacent vertices that have not been visited

• If yes, access this vertex, and then start from this vertex to access similar to the above

• If not, go back and search again. Repeat the appeal process until all vertices in the connected graph have been accessed

  Implementation of undirected graph depth traversal represented by adjacency matrix:

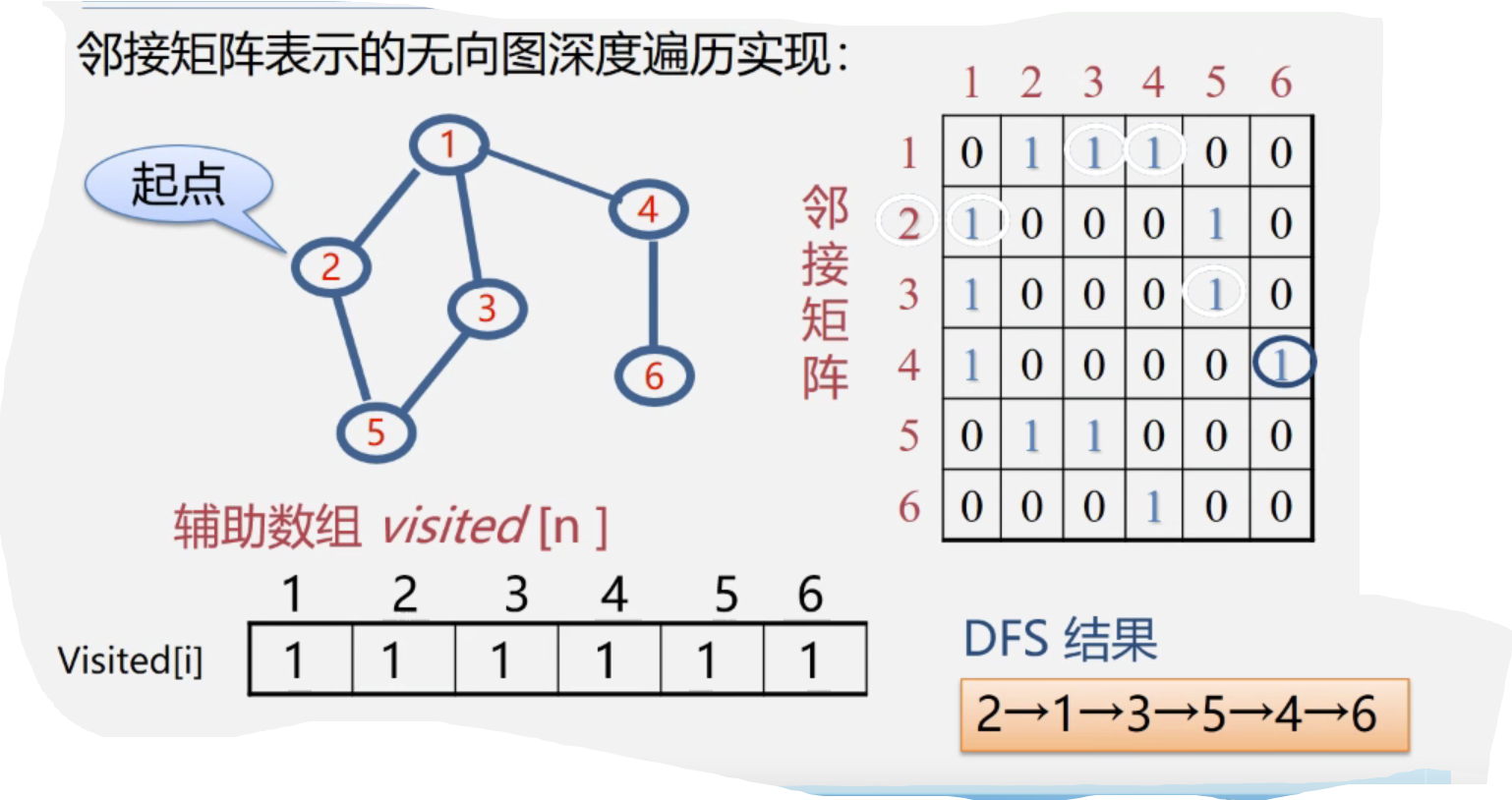
void DFS(AMGraph G,int v){//Figure G shows the type of adjacency matrix
cout<<v;visited[v]=true;//Access the v-th vertex
for(w=0;w<G.vexnum;w++)//Check the row of adjacency matrix v in turn
if((G.arcs[v][w]!=0)&&(!visited[w]))
DFS(G,w);//w is the critical point of v. if w is not accessed, DFS is called recursively
}

DFS algorithm efficiency analysis:

The graph is represented by adjacency matrix, and the time complexity is n*n

The time complexity of adjacency table representation graph is n+e

Breadth first traversal (BFS):
 

method:

Starting from a node of the graph, first access all the adjacent points v1,v2... Of the node in turn, and then access all the unreachable vertices adjacent to them in the order in which these vertices are accessed. Repeat this process to know that all vertices are accessed

 

void BFS(Graph G,int v)//Non recursive traversal of connected graph G by breadth first
{
cout<<v;visited[v]=ture;//Access the v-th vertex
InitQueue(Q);//Auxiliary queue Q initialization, null
EnQueue(Q,v);//v join the team
while(!QueueEmpty(Q))//Queue is not empty
{
DeQueue(Q,u);//The team head element is out of the team and set to u
for(w=FistAdjVex(G,u);w>=0;w=NextAdjVex(G,u,w))
 if(!visited[w]){//Adjacent vertices not yet accessed with w as u
cout<<w;visited[w]=ture;EnQueue(Q,w);//w into the team
}//if
}//while
}//BFS

Efficiency analysis:

If adjacency matrix is used, BFS will cycle a whole row for each accessed vertex. Time complexity: n*n

If adjacency table is used, the time complexity is n+e

Comparison of DFS and BFS algorithm efficiency:

The space complexity is the same, which is n,

The time complexity is only related to the storage structure, not the search path