1, AcWing 1125 Cattle travel
[Title Description]
Farmer John's farm has many pastoral areas, and some paths connect some specific pastoral areas.
A pastoral area with all the connections is called a pasture.
But for now, you can see that at least two pastoral areas are not connected.
Now, John wants to add a path to the farm (note that there is exactly one).
The diameter of a pasture is the distance between the two farthest pastoral areas in the pasture (all the distances mentioned in this topic refer to the shortest distance).
Consider the following two pastures, each of which has its own coordinates:
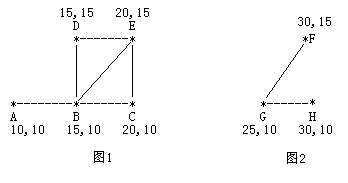
chart
1
1
1 yes
5
5
For pastures in 5 pastoral areas, the pastoral area is represented by * and the path is represented by a straight line.
chart
1
1
The diameter of the pasture shown in 1 is about
12.07106
12.07106
12.07106, the two farthest pastoral areas are
A
A
A and
E
E
E. The shortest path between them is
A
−
B
−
E
A-B-E
A−B−E.
chart
2
2
2 is another ranch.
Both pastures are on John's farm.
John will choose a pastoral area from each of the two pastures, and then connect it with a path to make the new and larger pastures have the smallest diameter after connection.
Note that if two paths intersect halfway, we don't think they are connected.
Only when two paths intersect in the same pastoral area, we think they are connected.
Now please find out a path connecting two different pastures by programming, so that after connecting this path, the diameter of the pastures with the largest diameter among all pastures (generated new pastures and original pastures) is as small as possible.
Output the smallest possible value of this diameter.
[input format]
The first
1
1
Line 1: an integer
N
N
N. Indicates the number of pastoral areas;
The first
2
2
2 to
N
+
1
N+1
N+1 line: two integers per line
X
,
Y
X,Y
10. Y, denotes
N
N
Coordinates of N pastoral areas. The coordinates of each pastoral area are different.
The first
N
+
2
N+2
Line N+2 to
2
∗
N
+
1
2*N+1
2 * N+1 line: each line includes
N
N
N numbers(
0
0
0 or
1
1
1) Represents a symmetric adjacency matrix.
For example, the matrices of the two pastures in the title description are described as follows:
A B C D E F G H A 0 1 0 0 0 0 0 0 B 1 0 1 1 1 0 0 0 C 0 1 0 0 1 0 0 0 D 0 1 0 0 1 0 0 0 E 0 1 1 1 0 0 0 0 F 0 0 0 0 0 0 1 0 G 0 0 0 0 0 1 0 1 H 0 0 0 0 0 0 1 0
The input data includes at least two disconnected pastoral areas.
[output format]
Only one line, including a real number, represents the answer.
The number retains six decimal places.
[data range]
1
≤
N
≤
150
1≤N≤150
1≤N≤150
0
≤
X
,
Y
≤
105
0≤X,Y≤105
0≤X,Y≤105
[input example]
8 10 10 15 10 20 10 15 15 20 15 30 15 25 10 30 10 01000000 10111000 01001000 01001000 01110000 00000010 00000101 00000010
[output example]
22.071068
[analysis]
Firstly, the shortest distance between any two points is obtained by Floyd algorithm d i s [ i ] [ j ] dis[i][j] dis[i][j], using arrays m a x d [ i ] maxd[i] maxd[i] represents and i i i connected and distance i i i the distance of the farthest point. For the diameter of the graph after edging, there are two cases:
- r e s res res for all m a x d [ i ] maxd[i] The maximum value in maxd[i], that is, the diameter of the new connected block formed by adding an edge between two non connected blocks is not larger than that of the original connected block;
- Enumerate which two points to add an edge between, i , j i,j i. J satisfied d i s [ i ] [ j ] ≥ I N F dis[i][j] \ge INF dis[i][j] ≥ INF, i.e i , j i,j i. J is not connected, and the diameter of the new connected block formed after edge addition is m a x d [ i ] + m a x d [ j ] + i And j of between of distance leave Maxd [i] + maxd [J] + distance between I and j Maxd [i] + maxd [J] + distance between I and j, r e s res res is the minimum value in all cases of edging.
[Code]
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
typedef pair<int, int> PII;
const int N = 160;
const double INF = 1e20;
char g[N][N];
double dis[N][N], maxd[N];//maxd[i] represents the distance from the point connected to I and farthest from I
PII q[N];
int n;
//Find the distance between two points
double get_dist(PII u, PII v)
{
return sqrt(pow(u.first - v.first, 2) + pow(u.second - v.second, 2));
}
int main()
{
cin >> n;
for (int i = 0; i < n; i++) cin >> q[i].first >> q[i].second;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
{
cin >> g[i][j];
if (i != j)
if (g[i][j] == '1') dis[i][j] = get_dist(q[i], q[j]);
else dis[i][j] = INF;
}
//Floyd algorithm calculates the distance between any two points
for (int k = 0; k < n; k++)
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
//Find maxd array
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
if (dis[i][j] < INF) maxd[i] = max(maxd[i], dis[i][j]);
double res = INF;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
if (dis[i][j] >= INF)//Judge the case of adding an edge between two unconnected points
res = min(res, maxd[i] + maxd[j] + get_dist(q[i], q[j]));
for (int i = 0; i < n; i++) res = max(res, maxd[i]);//Judge whether the diameter of each connected block is larger than the edge
printf("%lf\n", res);
return 0;
}