In graph theory search, single source BFS and multi-source BFS search distance.

1. BFS graph theory search question in leetcode

leetcode link: 1162. Map analysis

You now have a grid with a size of n x n, and each cell on it is marked with 0 and 1. Where 0 represents the ocean and 1 represents the land. Please find an ocean cell. The distance from the ocean cell to the nearest land cell is the largest. If there is only land or sea on the grid, return - 1.

The distance we are talking about here is the Manhattan Distance: the distance between the two cells (x0, y0) and (x1, y1) is | x0 - x1| + |y0 - y1|.

Example 1:

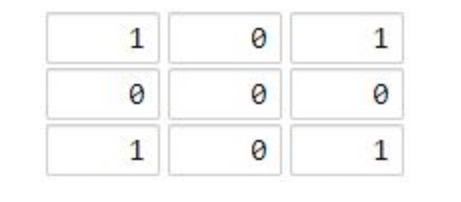
Input: grid = [[1,0,1],[0,0,0],[1,0,1]]
Output: 2
 Explanation: 
Ocean cell (1, 1) The distance between and all land cells is the maximum, and the maximum distance is 2.

Example 2:

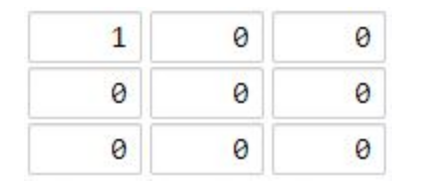
Input: grid = [[1,0,0],[0,0,0],[0,0,0]]
Output: 4
 Explanation: 
Ocean cell (2, 2) The distance from all land cells is the maximum, and the maximum distance is 4.

2. Single source BFS

Usually, we use BFS to find the shortest path, which is aimed at the following scenarios: starting from a specific starting point and solving the shortest distance to a specific end point.

This is a special kind of "single source shortest path" problem: the essence is to find the shortest path from a specific "source point" to a specific "sink point" on a graph with edge weight 1.

For this problem, if we apply the "single source shortest path" method, we need to do a BFS for each "ocean" location: find the nearest land distance of each "ocean", and then take it as the answer in all distances.

The worst case of a single BFS requires scanning a complete matrix with a complexity of max.

At the same time, up to n^2 marine areas need BFS, so the complexity of this method is O(n ^ 4), and O(n ^ 4) can be directly filled.

PS. the data range is 10 ^ 2. Theoretically, it will timeout, but the data of this question is weak, and Java 2021/06/28 can pass.

Some details: for convenience, when using the hash table to record the distance, we convert the two-dimensional coordinates (x, y) into the corresponding one-dimensional subscript idx = x * n + y and store it as a key.

Code implementation:

class Solution {
    public int maxDistance(int[][] grid) {
        int n = grid.length;
        int ans = -1;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 0) {
                    ans = Math.max(ans, bfs(n, i, j, grid));
                }
            }
        }
        return ans;
    }
    // Single BFS: solve the land distance closest to the ocean position (x,y)
    public int bfs(int n, int x, int y, int[][] grid) {
        int[][] dirs = new int[][]{{1,0},{-1,0},{0,1},{0,-1}};
        Deque<int[]> queue = new ArrayDeque<>();
        Map<Integer, Integer> map = new HashMap<>();
        queue.addLast(new int[]{x, y});
        map.put(x * n + y, 0);
        while (!queue.isEmpty()) {
            int[] poll = queue.pollFirst();
            int dx = poll[0], dy = poll[1];
            int step = map.get(dx * n + dy);
            if (grid[dx][dy] == 1) return step;
            for (int[] di : dirs) {
                int nx = dx + di[0], ny = dy + di[1];
                if (nx < 0 || nx >= n || ny < 0 || ny >= n) continue;
                int key = nx * n + ny;
                if (map.containsKey(key)) continue;
                queue.addLast(new int[]{nx, ny});
                map.put(key, step + 1);
            }
        }
        return -1;
    } 
}

3. Multi source BFS

This is actually an introductory question of "multi-source BFS".

Different from "single source shortest path", the "multi-source shortest path" problem is to find the shortest path from "multiple source points" to "one / more sink points".

In terms of implementation, the core search part, "multi-source BFS" is no different from "single source BFS".

By creating a "virtual source point", we can convert "multi-source BFS" to "single source BFS".

what do you mean?

Taking this problem as an example, the problem asks us to find the maximum value from each "ocean" area to the nearest "land" area.

We can reverse the "source / start point" and "sink / end point": starting from each "land" area, multiple "land" areas yearn to spread one circle at a time. The number of circles corresponding to the first coverage of each "ocean" area is the distance from the "ocean" area to the nearest "land" area.

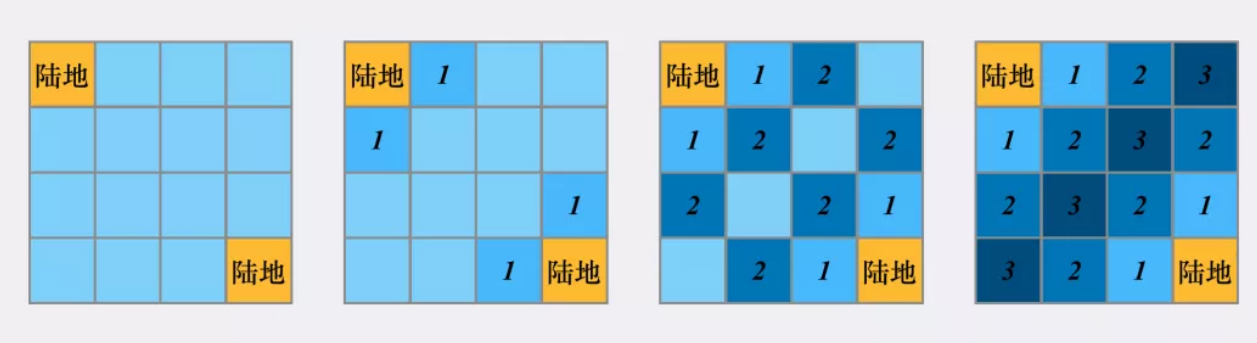
However, how does this relate to "single source BFS"?

We can imagine that there is a "virtual source point", which has equal weight edges with all "real source points" (land). Then the shortest path between any "ocean" area and "nearest land" area is equivalent to the shortest path with "virtual source point":

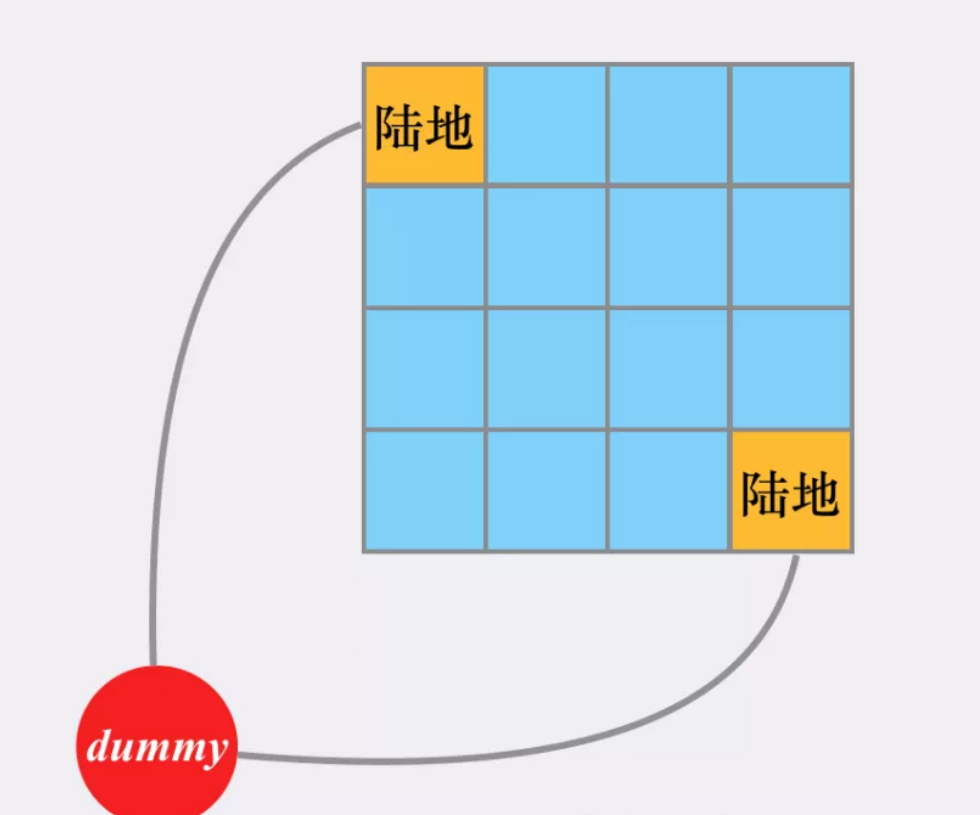
In terms of implementation, we do not need to really establish this virtual source point, but just join all "real source points" in the team before BFS.

This process is equivalent to popping up the "virtual source point" from the queue, joining the point it can reach (the real source point), and then performing the conventional BFS.

Some details: for convenience in implementation, if an "ocean" area is accessed during conventional BFS, it indicates that it is covered by the "nearest land" from it, and the modified value is the minimum distance. In this way, we only need to consider those "ocean" areas whose value is still (representing that they have not been updated).

Code implementation:

class Solution {
    public int maxDistance(int[][] grid) {
        int n = grid.length;
        Deque<int[]> d = new ArrayDeque<>();
        Map<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 1) {
                    d.add(new int[]{i, j});
                    map.put(i * n + j, 0);
                }
            }
        }
        int ans = -1;
        int[][] dirs = new int[][]{{1,0},{-1,0},{0,1},{0,-1}};
        while (!d.isEmpty()) {
            int[] poll = d.poll();
            int dx = poll[0], dy = poll[1];
            int step = map.get(dx * n + dy);
            for (int[] di : dirs) {
                int nx = dx + di[0], ny = dy + di[1];
                if (nx < 0 || nx >= n || ny < 0 || ny >= n) continue;
                if (grid[nx][ny] != 0) continue;
                grid[nx][ny] = step + 1;
                d.add(new int[]{nx, ny});
                map.put(nx * n + ny, step + 1);
                ans = Math.max(ans, step + 1);
            }
        }
        return ans;
    }
}

4. Multi source BFS expansion

leetcode title link: 1765. The highest point in the map

Title Description:

Give you an integer matrix isWater with the size of m x n, which represents a map composed of land and water cells.

• If isWater[i][j] == 0, the grid (i, j) is a land grid.
• If isWater[i][j] == 1, grid (i, j) is a water grid.

You need to arrange the height of each cell according to the following rules:

• The height of each lattice must be nonnegative.
• If a grid is a water area, its height must be 0.
• The height difference of any adjacent grid is at most 1. When two grids are close to each other in due east, South, West and North, they are called adjacent grids. (that is, they have a common edge)

Find a scheme to arrange the height so that the highest height value in the matrix is the largest.

Please return an integer matrix height of size m x n, where height[i][j] is the height of lattice (i, j). If there are multiple solutions, please return any one.

Solution:

The title stipulates that the height of the water area is 0, and then the height difference between adjacent grids is at most 1,

We can join the team in all water areas (height 0), and then run BFS once.

The operation of joining all water areas (height 0) can be regarded as joining the nodes linked to the "virtual source point" (also equivalent to joining only the virtual source point at the beginning):

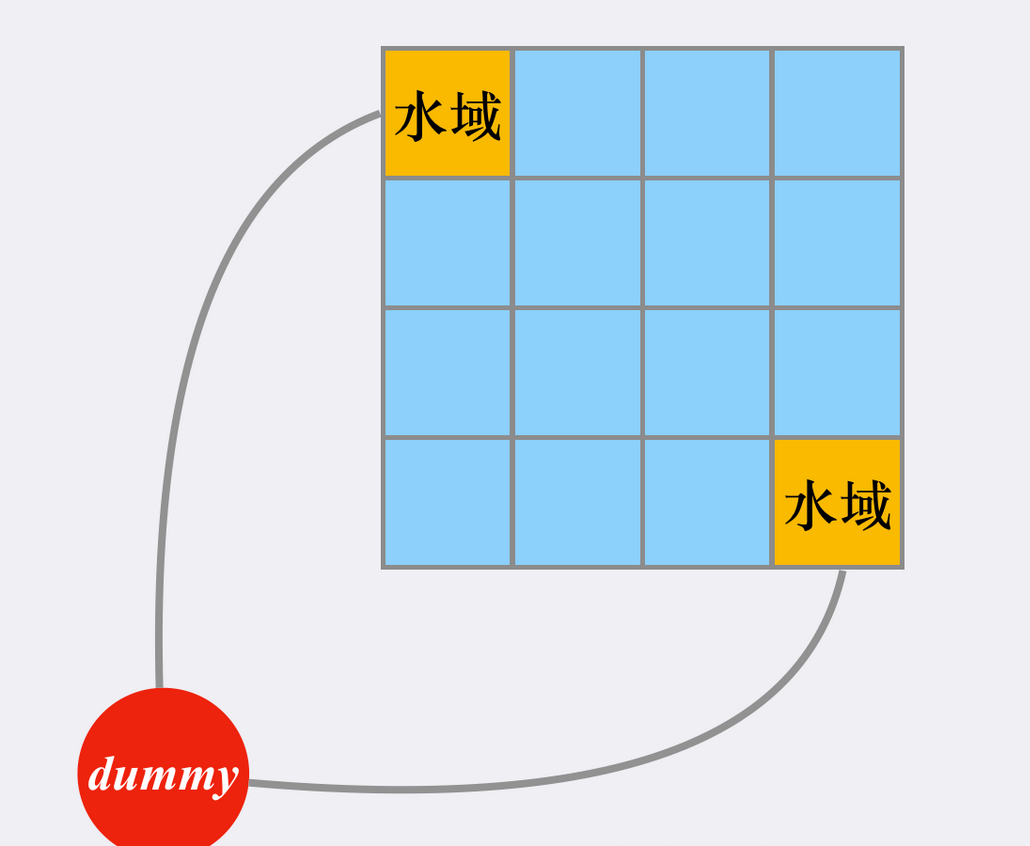
It is easy to prove the correctness of this approach: for a "land" area (with variable height), the height it can fill depends on its distance from other "water" areas, and we finally want to make the whole answer matrix legal. Therefore, each "land" area should take the "lower bound" of the height it can fill, That is, it is only updated by the area of "the nearest water area", which is in line with the nature of BFS.

Code implementation:

class Solution {
    public int[][] highestPeak(int[][] isWater) {
        int m = isWater.length, n = isWater[0].length;
        int[][] ans = new int[m][n];
        Deque<int[]> d = new ArrayDeque<>();
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (isWater[i][j] == 1) d.addLast(new int[]{i, j});
                ans[i][j] = isWater[i][j] == 1 ? 0 : -1;
            }
        }
        int[][] dirs = new int[][]{{1,0},{-1,0},{0,1},{0,-1}};
        while (!d.isEmpty()) {
            int[] info = d.pollFirst();
            int x = info[0], y = info[1];
            for (int[] di : dirs) {
                int nx = x + di[0], ny = y + di[1];
                if (nx < 0 || nx >= m || ny < 0 || ny >= n) continue;
                if (ans[nx][ny] != -1) continue;
                ans[nx][ny] = ans[x][y] + 1;
                d.addLast(new int[]{nx, ny});
            }
        }
        return ans;
    }
}

5. Summary

"Multi source BFS". By creating a "virtual source point", we can convert it back to a "single source BFS" problem.

In terms of implementation, we only need to join all "real points" in the team, and then conduct BFS.

It seems that there is little difference between the two, but its essence is to convert multiple simple BFS into one BFS by using conventional Flood Fill through source / sink conversion, which can effectively reduce the time complexity of our algorithm.

reference resources:

[graph theory search topics] how to use "multi-source BFS" to reduce time complexity