Graphical analysis of Vue3 diff algorithm

Hello, I'm jiandarui. This article mainly analyzes Vue3 diff algorithm. Through this article, you can know:

• diff's main process, core logic
• How does diff reuse, move and unload nodes
• And there is an example, which can be analyzed in combination with this paper

If you don't particularly understand the patch process of Vnode and renderer, it is recommended to read the following two articles first:

• Vnode
• Renderer analysis

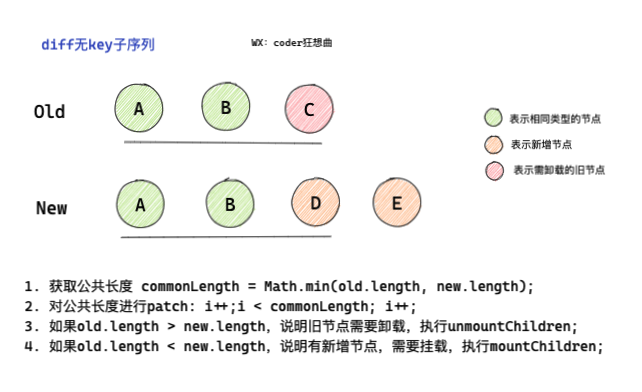
1.0 diff no key child node

Marked as unlocked in processing_ Fragment.

• First, the minimum common length commonLength will be obtained through the new and old subsequences.
• Loop through the patch on the common part.
• After the patch is completed, the remaining old and new nodes will be processed.
• If oldlength > newlength, unmount the old node

• Otherwise, it indicates that there are new nodes and mount is required;

  

The omitted code is pasted here.

const patchUnkeyedChildren = (c1, c2,...res) => {
    c1 = c1 || EMPTY_ARR
    c2 = c2 || EMPTY_ARR
    // Gets the length of the old and new child nodes
    const oldLength = c1.length
    const newLength = c2.length
    // 1. Obtain the common length. Minimum length
    const commonLength = Math.min(oldLength, newLength)
    let i
    // 2. patch public part
    for (i = 0; i < commonLength; i++) { 
      patch(...)
    }
    // 3. Uninstall old nodes
    if (oldLength > newLength) {
      // remove old
      unmountChildren(...)
    } else {
      // mount new
      // 4. Otherwise, mount the new child node
      mountChildren(...)
    }
  }

From the above code, we can see that the logic is very simple and rough when dealing with keyless child nodes. To be exact, the efficiency of dealing with keyless child nodes is not high.

Because whether it is to directly patch the public part or the newly added node, mountChildren (actually traversing child nodes and performing patch operations) is actually a recursive patch, which will affect the performance.

2.0 diff has key child node sequence

When diff has a key subsequence, it will be subdivided. It will be judged by one of the following situations:

• The starting position is the same as the node type.
• The end position is the same as the node type.
• After adding nodes, the processing is the same.
• After the same part is processed, there are old nodes that need to be unloaded.
• The beginning and end are the same, but there are reusable out of order nodes in the middle.

At the beginning, Mr. Hui made three corrections, namely:

• i = 0, pointing to the beginning of the old and new sequence
• e1 = oldLength - 1, pointing to the end of the old sequence
• e2 = newLength - 1, pointing to the end of the new sequence

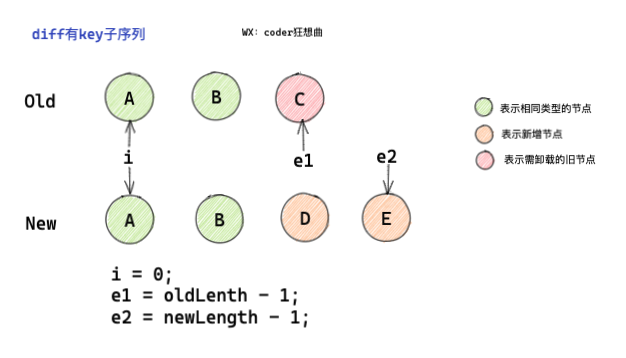
let i = 0
const l2 = c2.length
let e1 = c1.length - 1 // prev ending index
let e2 = l2 - 1 // next ending index

Let's start diff processing by case.

2.1 the starting position node type is the same

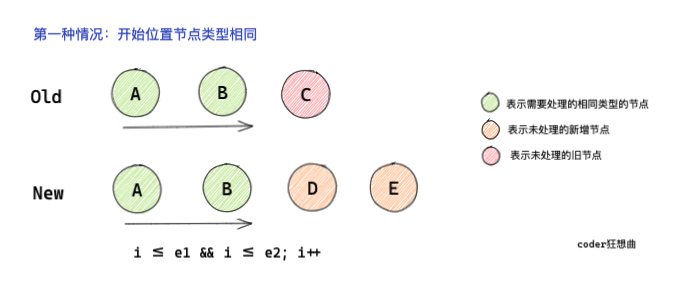
• For nodes with the same starting position type, diff traversal is performed from left to right.
• If the old and new nodes are of the same type, patch them
• If the node types are different, break and jump out of the traversal diff

//  i <= 2 && i <= 3
while (i <= e1 && i <= e2) {
  const n1 = c1[i]
  const n2 = c2[i]
  if (isSameVNodeType(n1, n2)) {
    // If it is the same node type, recursive patch is performed
    patch(...)
  } else {
    // Otherwise exit
    break
  }
  i++
}

Part of the code is omitted above, but it does not affect the main logic.

It can be seen from the code that during traversal, the three pointers previously declared in the global context of the function are used for traversal judgment.

Ensure that it can fully traverse to the same position as the starting position, I < = E1 & & I < = E2.

Once you encounter nodes of different types, you will jump out of diff traversal.

2.2 the end position node type is the same

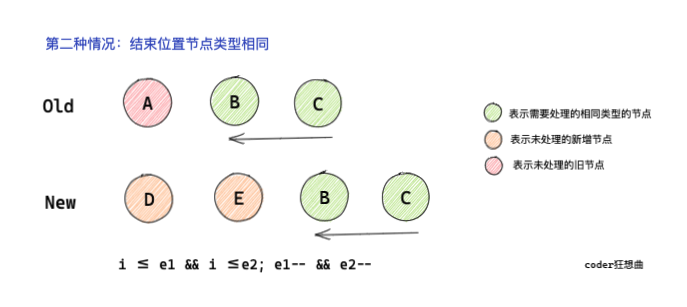
The start position is the same, and the end of diff will be followed by traversing diff from the end of the sequence.

At this time, the tail pointers e1 and e2 need to be decremented.

//  i <= 2 && i <= 3
// After: E1 = 0 E2 = 1
while (i <= e1 && i <= e2) {
  const n1 = c1[e1]
  const n2 = c2[e2]
  if (isSameVNodeType(n1, n2)) {
    // Same node type
    patch(...)
  } else {
    // Otherwise exit
    break
  }
  e1--
  e2--
}

It can be seen from the code that diff logic is basically the same as the first one, and the same type is used for patch processing.

Different types of break, jump out of loop traversal.

And decrement the tail pointer.

2.3 after traversing the same part, there are new nodes in the new sequence for mounting

After the processing of the above two cases, the nodes with the same part at the beginning and end have been patched. The next step is to patch the new nodes in the new sequence.

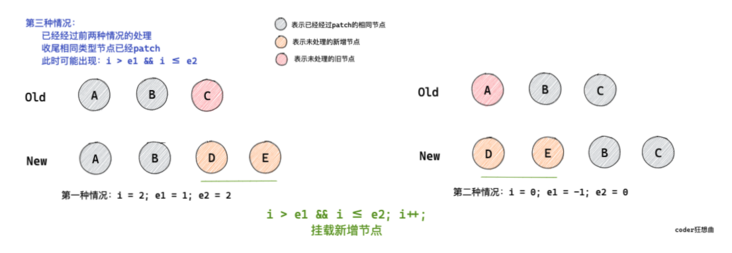
After the above two payment requests, if there are new nodes, I > E1 & & I < = E2 may occur.

In this case, it means that there are new nodes in the new child node sequence.

The new node will be patch ed.

// 3. common sequence + mount
// (a b)
// (a b) c
// i = 2, e1 = 1, e2 = 2
// (a b)
// c (a b)
// i = 0, e1 = -1, e2 = 0
if (i > e1) {
  if (i <= e2) {
    const nextPos = e2 + 1
    // NextPos < L2 indicates that there are tail nodes that have been patch ed,
    // Otherwise, the parent node is obtained as the anchor
    const anchor = nextPos < l2 ? c2[nextPos].el : parentAnchor
    while (i <= e2) {
      patch(null, c2[i], anchor, ...others)
      i++
    }
  }
}

As can be seen from the above code, the first parameter is not passed during patch, and the mount logic will eventually be used.

You can read this article It mainly analyzes the process of patch

During the process of patch, the i pointer is incremented.

And get the anchor point through nextPos.

If NextPos < L2, the node that has been patch ed is used as the anchor point; otherwise, the parent node is used as the anchor point.

2.4 after traversing the same part, unload the new sequence with fewer nodes

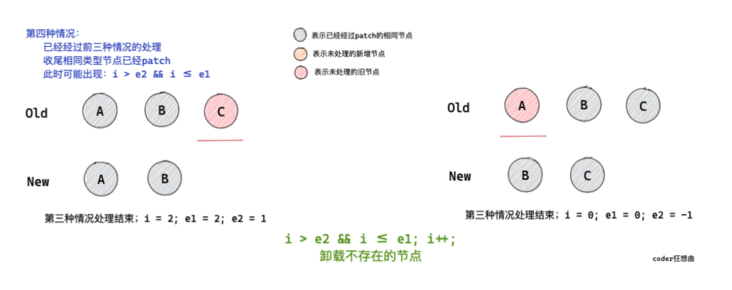
If I > E2 & & I < = E1 occurs after processing the same ending nodes, it means that there are old nodes that need to be unloaded.

// 4. common sequence + unmount
// (a b) c
// (a b)
// i = 2, e1 = 2, e2 = 1
// a (b c)
// (b c)
// i = 0, e1 = 0, e2 = -1
// Common sequence unload old
else if (i > e2) {
  while (i <= e1) {
    unmount(c1[i], parentComponent, parentSuspense, true)
    i++
  }
}

You can know from the code that in this case, the i pointer will be incremented to unload the old node.

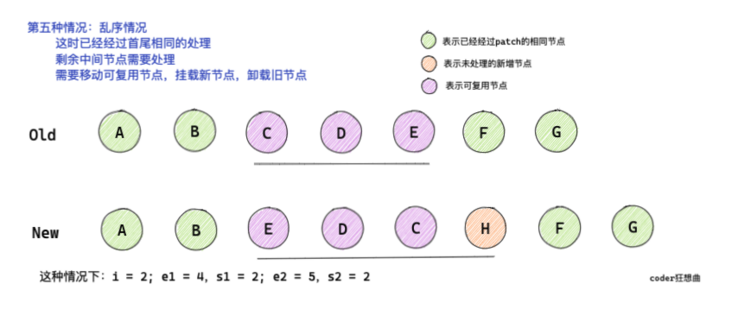
2.5 disorder

In this case, it is more complicated, but the core logic of diff is to build a maximum increasing subsequence through the position change of old and new nodes. The maximum subsequence can ensure the reuse of nodes through the minimum movement or patch.

Let's take a look at how to implement it.

2.5.1 build key:index mapping for new child nodes

// 5. Disorder
// [i ... e1 + 1]: a b [c d e] f g
// [i ... e2 + 1]: a b [e d c h] f g
// i = 2, e1 = 4, e2 = 5

const s1 = i // s1 = 2
const s2 = i // s2 = 2

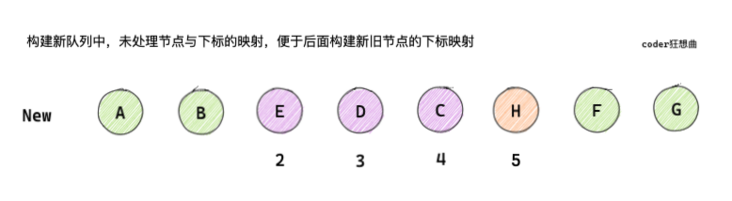
// 5.1 build key:index map for newChildren
// Firstly, the mapping of key: index in the new subsequence is constructed for the new child nodes
// New child nodes created by map
const keyToNewIndexMap = new Map()
// Traverse the new node and set the key for the new node
// i = 2; i <= 5
for (i = s2; i <= e2; i++) {
  // Gets the child nodes in the new sequence
  const nextChild = c2[i];
  if (nextChild.key != null) {
    // nextChild.key already exists
    // a b [e d c h] f g
    // e:2 d:3 c:4 h:5
    keyToNewIndexMap.set(nextChild.key, i)
  }
}

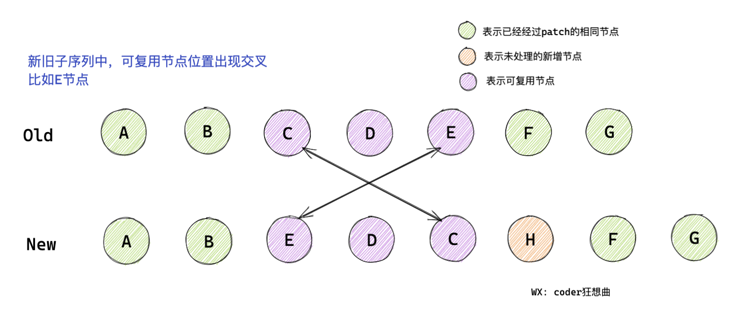
Combined with the above figure and code, you can know:

• After the same patch processing, i = 2, e1 = 4, e2 = 5
• After traversal, in the keyToNewIndexMap, the key:index relationship of the new node is e: 2, D: 3, C: 4, H: 5
• keyToNewIndexMap is mainly used to determine the position of reusable nodes in the new subsequence by traversing the old subsequence

2.5.2 traverse the old subsequence from left to right, patch the matching nodes of the same type, and remove the nonexistent nodes

After the previous processing, the keyToNewIndexMap has been created.

Before starting the left to right traversal, you need to know the meaning of several variables:

// 5.2 loop through old children left to be patched and try to patch
// matching nodes & remove nodes that are no longer present
// Start from the left side of the old child node and cycle through the patch.
// And patch the matching nodes and remove the nonexistent nodes

// Number of nodes that have been patch ed
let patched = 0
// Number of nodes requiring patch
// The above figure is an example: e2 = 5; s2 = 2;  Know the number of nodes that need patch
// toBePatched = 4
const toBePatched = e2 - s2 + 1
// Used to determine whether the node needs to be moved
// moved = true when reusable nodes cross in the old and new queues
let moved = false
// used to track whether any node has moved
// Used to record whether the node has been moved
let maxNewIndexSoFar = 0

// works as Map<newIndex, oldIndex>
// Make subscript mapping between old and new nodes
// Note that oldIndex is offset by +1
// Note that the index of the old node should be offset by a subscript to the right

// and oldIndex = 0 is a special value indicating the new node has
// no corresponding old node.
// And the old node Index = 0 is a special value used to indicate that there is no corresponding old node in the new node

// used for determining longest stable subsequence
// newIndexToOldIndexMap is used to determine the longest increment subsequence
// map of new subscript and old subscript
const newIndexToOldIndexMap = new Array(toBePatched)
// Initialize all values to 0
// [0, 0, 0, 0]
for (i = 0; i < toBePatched; i++) newIndexToOldIndexMap[i] = 0

• The variable patched is used to record the nodes that have been patched
• The variable toBePatched is used to record the number of nodes that need to be patched
• The variable moved is used to record whether there are reusable nodes crossing
• maxNewIndexSoFar is used to record when there is a child node without a key in the old subsequence, but the child node appears in the new subsequence and can be reused with the maximum subscript.
• The variable newIndexToOldIndexMap is used to map the subscripts of the nodes in the new subsequence, corresponding to the subscripts of the nodes in the old subsequence
• And the newIndexToOldIndexMap will be initialized to an all 0 array, [0, 0, 0, 0]

After knowing the meaning of these variables, we can start traversing the subsequence from left to right.

When traversing, you need to traverse the old subsequence first, starting from s1 and ending at e1.

patched will be accumulated during traversal.

Uninstall old nodes

If patched > = tobepatched, the number of child nodes in the new subsequence is less than that in the old subsequence.

The old child node needs to be unloaded.

// Traversing the child nodes of the unprocessed old sequence
for (i = s1; i <= e1; i++) {
    // Get old node
    // Will get c d e one by one
    const prevChild = c1[i]
    // If the number of patched nodes > = the number of nodes to be patched
    
    // patched was initially 0
    // patched >= 4
    if (patched >= toBePatched) {
      // all new children have been patched so this can only be a removal
      // This indicates that all new nodes have been patch ed, so the old nodes can be removed
      unmount(prevChild, parentComponent, parentSuspense, true)
      continue
    }
}

If prevChild The key exists, and the subscript newIndex of prevChild in the new subsequence will be obtained through the keyToNewIndexMap we built earlier.

Get newIndex

// New node subscript
let newIndex
if (prevChild.key != null) {
  // The old node must have a key, 
  // Obtain the corresponding node position of the new child node of the same type in the new queue according to the old node key
  // At this time, because c d e is the original node and has a key
  // h is the new node. If the old node does not get the corresponding index, it will go else
  // So newIndex will start with the following situations
  /**
   * node  newIndex
   *  c       4
   *  d       3
   *  e       2
   * */ 
  // Here you can get the newIndex
  newIndex = keyToNewIndexMap.get(prevChild.key)
}

Taking the figure as an example, it can be seen that in the traversal process, nodes c, d and e are reusable nodes, corresponding to the positions of 2, 3 and 4 in the new sub sequence respectively.

Therefore, the values newIndex can get are 4, 3 and 2.

What if the old node does not have a key?

// key-less node, try to locate a key-less node of the same type
// If the old node does not have a key
// The location of new nodes of the same type without key in the new node queue will be found
// j = 2: j <= 5
for (j = s2; j <= e2; j++) {
  if (
    newIndexToOldIndexMap[j - s2] === 0 &&
    // Judge whether the old and new nodes are the same
    isSameVNodeType(prevChild, c2[j])
  ) {
    // Get subscripts of nodes of the same type
    newIndex = j
    break
  }
}

If the node does not have a key, it will also take the new sub sequence, traverse and find two sub nodes with the same old and new types without a key, and take the subscript of this node as the newIndex.

Newindextooldindexmap [J - S2] = = 0 indicates that the node does not have a key.

If newIndex has not been obtained, it indicates that there is no child node in the new subsequence that is the same as prevChild, and prevChild needs to be unloaded.

if (newIndex === undefined) {
  // There is no corresponding new node to uninstall the old one
  unmount(prevChild, parentComponent, parentSuspense, true)
}

Otherwise, start to build a keyToNewIndexMap according to the newIndex to specify the subscript position corresponding to the old and new nodes.

Keep in mind that newIndex is obtained from the old node and its subscript in the new subsequence.

// The newIndex obtained is processed here
// Start sorting out the mapping of new node subscript Index to old nodes of the same type in the old queue
// The new node subscript starts from s2=2, and the corresponding old node subscript needs to be offset by one subscript
// 0 indicates that the current node has no corresponding old node
// Offset 1 position, i starts from s1 = 2, s2 = 2
// 4 - 2 obtain subscript 2, and the new c node corresponds to the position subscript 3 of the old c node
// 3 - 2 obtain subscript 1, and the new d node corresponds to the position subscript 4 of the old D node
// 2 - 2 get the subscript 0, and the new e node corresponds to the subscript 5 of the old e node
// [0, 0, 0, 0] => [5, 4, 3, 0]
// [2,3,4,5] = [5, 4, 3, 0]
newIndexToOldIndexMap[newIndex - s2] = i + 1
// newIndex will take 4 3 2
/** 
 *   newIndex  maxNewIndexSoFar   moved
 *       4            0          false
 *       3            4           true
 *       2        
 * 
 * */ 
if (newIndex >= maxNewIndexSoFar) {
  maxNewIndexSoFar = newIndex
} else {
  moved = true
}

While building the newIndexToOldIndexMap, it will determine whether the node moves by judging the relationship between newIndex and maxNewIndexSoFa.

The last traversal end of newIndexToOldIndexMap should be [5, 4, 3, 0]. 0 indicates that there is no corresponding node in the old sequence and the node may be a new node.

If the relative position of the old and new nodes in the sequence remains unchanged, maxNewIndexSoFar will increase with the increase of newIndex.

This means that the nodes do not cross. There is no need to move reusable nodes.

Otherwise, the reusable node moves, and the reusable node needs to be moved.

At the end of traversal, the old and new nodes will be patched, and the patched will be accumulated to record how many nodes have been processed.

// Recursive patch
/**
 * old   new
 *  c     c
 *  d     d
 *  e     e 
*/
patch(
  prevChild,
  c2[newIndex],
  container,
  null,
  parentComponent,
  parentSuspense,
  isSVG,
  slotScopeIds,
  optimized
)
// Already patch ed
patched++

After the above processing, the old nodes have been unloaded and the child nodes whose relative positions remain unchanged have been patch reused.

The next step is to move the reusable nodes and mount the new nodes in the new subsequence.

2.5.3 move reusable nodes and mount new nodes

This involves a core piece of code, which is also the key to improving Vue3 diff efficiency.

The subscript mapping before and after the change of new and old child nodes is recorded through newIndexToOldIndexMap.

Here, we will get a maximum increasing subsequence through the getSequence method. Used to record the subscript of the child node whose relative position has not changed.

According to this incremental sub sequence, when moving reusable nodes, only the sub nodes whose relative position changes before and after can be moved.

Make minimal changes.

What is the largest increasing subsequence?

• A subsequence is a sequence derived from an array. It deletes (or does not delete) the elements in the array without changing the order of the remaining elements.
• The increasing subsequence is a subsequence derived from the array, and each element maintains an increasing relationship one by one.
• For example:
• Array [3, 6, 2, 7] is the longest strictly increasing subsequence of array [0, 3, 1, 6, 2, 2, 7].
• Array [2, 3, 7, 101] is the largest increasing subsequence of array [10, 9, 2, 5, 3, 7, 101, 18].
• Array [0, 1, 2, 3] is the largest increasing subsequence of array [0, 1, 0, 3, 2, 3].

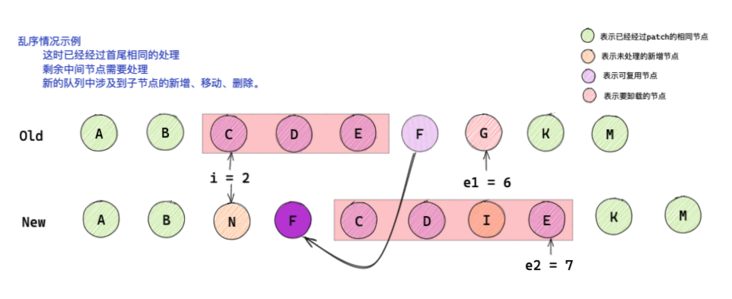
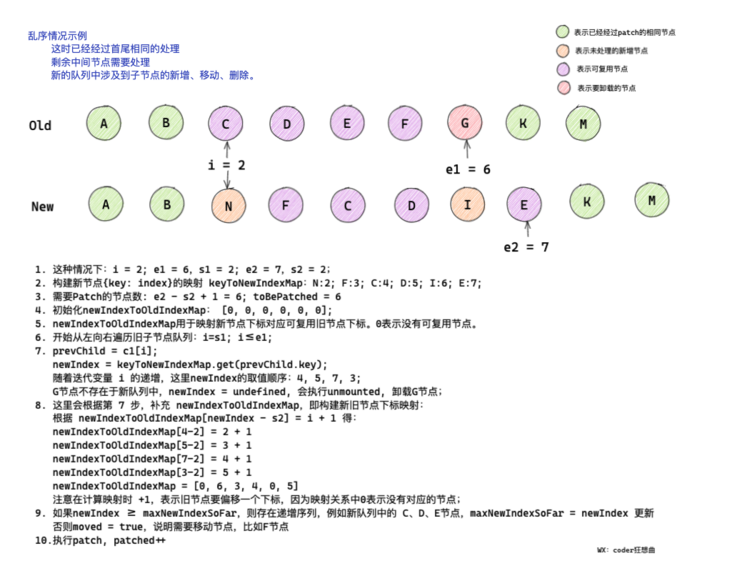
Taking the above figure as an example, among the unprocessed out of order nodes, there are new nodes N and I, node G to be unloaded, and reusable nodes C, D, E and F.

There is no change in the relative position of node CDE in the new and old subsequence. If we want to realize node reuse through minimum change, we can find out the subscript position of node F before and after the change, and insert node F before node C in the new subsequence.

The function of the maximum incremental subsequence is to create an incremental array through the mapping between the old and new nodes before and after the change, so that you can know which nodes have not changed in relative position before and after the change, and which nodes need to be moved.

The difference between the incremental subsequence in Vue3 is that it saves the subscript of the reusable node in the newIndexToOldIndexMap. Not the element in newIndexToOldIndexMap.

Next, let's look at the code:

// 5.3 move and mount
// generate longest stable subsequence only when nodes have moved
// Mobile node mount node
// The longest incremental subsequence is generated only when the node is moved
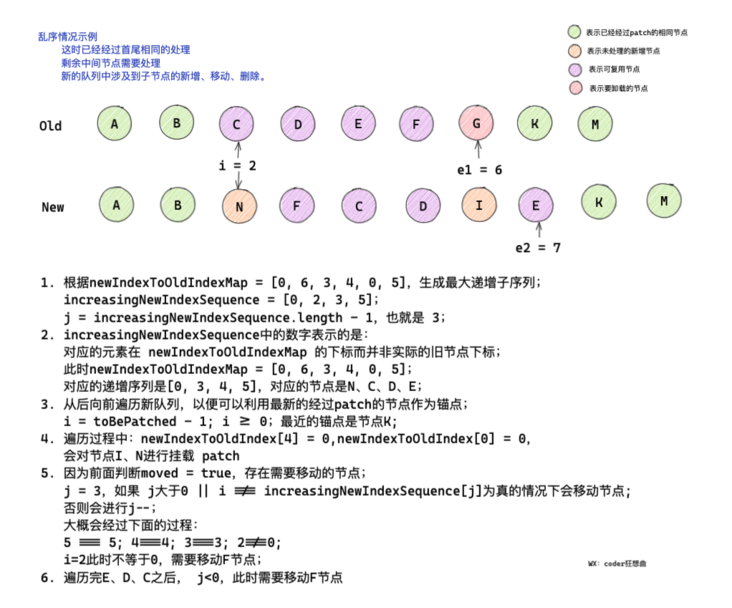
// After the above operation, newIndexToOldIndexMap = [5, 4, 3, 0]
// Get increasing newindexsequence = [2]
const increasingNewIndexSequence = moved
  ? getSequence(newIndexToOldIndexMap)
  : EMPTY_ARR
// j = 0
j = increasingNewIndexSequence.length - 1
// looping backwards so that we can use last patched node as anchor
// Traverse from back to front so that you can use the latest patch ed node as the anchor point
// i = 3
for (i = toBePatched - 1; i >= 0; i--) {
  // 5 4 3 2
  const nextIndex = s2 + i
  // Node H C D E 
  const nextChild = c2[nextIndex]
  // Get anchor
  const anchor =
    nextIndex + 1 < l2 ? c2[nextIndex + 1].el : parentAnchor
  // [5, 4, 3, 0] node h will be patch ed, which is actually mount
  //  C D E will be moved
  if (newIndexToOldIndexMap[i] === 0) {
    // mount new
    // Mount new
    patch(
      null,
      nextChild,
      container,
      anchor,
      ...
    )
  } else if (moved) {
    // move if:
    // There is no stable subsequence (e.g. a reverse)
    // OR current node is not among the stable sequence
    // If there is no longest increment subsequence or the current node is not in the middle of the increment subsequence
    // Then move the node
    // 
    if (j < 0 || i !== increasingNewIndexSequence[j]) {
      move(nextChild, container, anchor, MoveType.REORDER)
    } else {
      j--
    }
  }
}

You can know from the above code:

• The maximum increment subsequence obtained by newIndexToOldIndexMap is [2]
• j = 0
• Traverse from right to left when traversing, so as to obtain the anchor point. If there is a brother node that has been patch ed, the brother node is used as the anchor point; otherwise, the parent node is used as the anchor point
• [oldMap] = = = [oldMap] = = [oldnew] node description. You need to mount the node. In this case, you only need to pass null to the first parameter of patch. You can know that the h node will be patched first.
• Otherwise, it will judge whether moved is true. Through the previous analysis, we know that the position of node C & node E has moved in the forward and backward changes.
• Therefore, the node will be moved here. We know that j is 0 and i is 2, i== If increasing newindexsequence [J] is true, the C node will not be moved, but j --.
• Later, because J < 0, nodes D and E will be moved.

So far, we have completed the learning analysis of Vue3 diff algorithm.

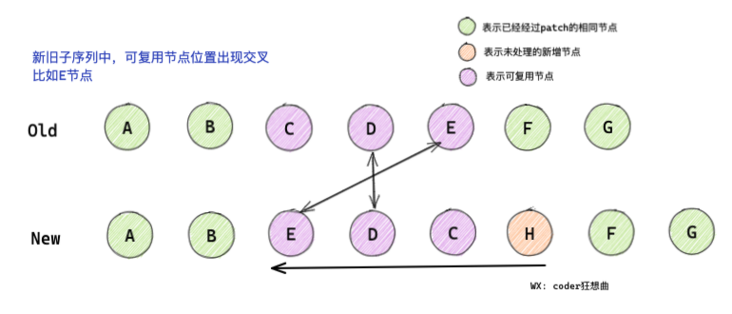
Here is an example for you to practice in combination with the analysis process of this article:

You can only look at the first picture for analysis. After the analysis, you can compare it with the second and third pictures.

Figure 1:

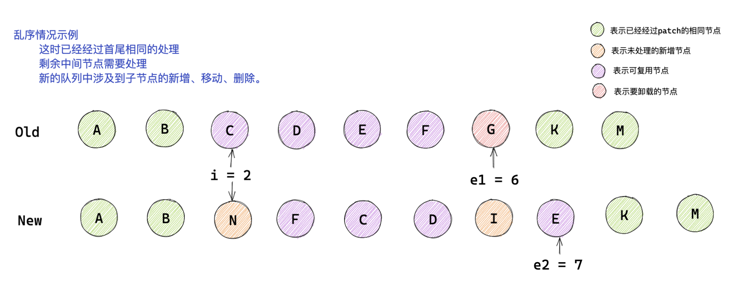
Figure 2 & 3:

summary

Through the above learning analysis, we can know that Vue3's diff algorithm will first finish the patch processing of the same node. After that, it will mount the new node and unload the old node.

If the subsequence is complex, such as out of order, the reusable nodes will be found first, and a maximum incremental subsequence will be constructed through the location mapping of reusable nodes, and the nodes will be mounted & moved through the maximum incremental subsequence. To improve diff efficiency and maximize the possibility of node reuse.