Guangzhou University ACM2021 Week 11 training
Gossip: I haven't played weekly games for a long time (actually not). I went online for three hours in five hours. On the whole, the first five questions are very simple, but they haven't been handled well in the details, which is a test of my mentality. Finally, question a4. After reading the fifth question, you will have something to run away from. However, it is also a violent enumeration question, which is just a little bit compressed.
A - transaction Gym - 102890I
meaning of the title

The general meaning is to buy three books (read into n books at the beginning). The price is given and can be combined to pay according to needs. There is a discount here, that is, reduce 100 from 500.
Problem solution
Since the title says 500 minus 100, try to gather more than 500 groups for a long time. We can sort them first, and then record the total price in a group from small to large. When the sum is greater than or equal to 500, we can divide them into a group. Because there are only three books here, it is very simple. Even enumeration can be used. The method here should be used for n.
code
using namespace std;
const int N=1e5;
int a[N];
int main()
{
//IOS
int d;
int cnt=0;
while(cin>>d){
a[cnt++]=d;
}
sort(a,a+cnt);
ll ans=0;
int i=0;
ll t=0;
for(;i<cnt&&a[i]<500;i++){
t+=a[i];
if(t>=500){
ans+=(t-100);t=0;
}
}
if(t>0){
ans+=t;
}
for(;i<cnt;i++)ans+=(a[i]-100);
cout<<ans<<'\n';
return 0;
}
B - Triangle Gym - 102890C
meaning of the title

The number of triangles is required. There was originally a big triangle, but now it is cutting n lines from the bottom, and then cutting k lines parallel to the ground. How many different triangles can be included at this time. There are t sets of samples in total.
Problem solution
First of all, it is easy to find that one vertex of the triangle is determined. If you cut k knives in parallel, you have to traverse the bottom edge when counting, so here are k+1 bottom edges, and the situation of each side is the same, that is, count one of them and multiply by k+1.
For each group of edges, the N cutter is divided into n+1 small triangles, and several adjacent small triangles can form a large triangle. Therefore, starting from the size of the triangle, there should be n+1, N, n-1, ~ ~, which is added to n-p=0, that is, the largest triangle, i.e. n+1. Obviously, it's the arithmetic sequence 1 added to n+1. The answer is multiplied by k+1.
Here wa is a lot of times, because I noticed that the answer should be mod1e7, and I put / 2 at the end of the arithmetic sequence to calculate, which is completely icing on the cake. Because the result of the arithmetic sequence (it is easy to find that it must be an odd number multiplied by an even number) takes the module, its parity changes. If you go to / 2 later, there will be an error. You should take the module honestly / 2.
code
using namespace std;
const int N=1e5;
const ll mod=1000000007;
int a[N];
int main()
{
//IOS
int t;cin>>t;
while(t--)
{
ll n,k;
cin>>k>>n;
ll ans=(((k+1)*(k+2)/2)%mod*(n+1))%mod;
cout<<ans<<'\n';
}
return 0;
}
C - formula AtCoder - arc061_a
meaning of the title
Give you a string s containing only 1 ~ 9, and the length of the string is less than 10. You can insert "+" between any two letters to make it a legal formula. You can not insert a "+" sign and ask you the sum of all legal formulas
Problem solution
The string is very short. You can add or not add a plus sign everywhere. When enumerating binary compression.
code
using namespace std;
const int N=122;
const ll mod=1000000007;
ll dp[12][12];
int main()
{
//IOS
string s;cin>>s;
int len=s.length();
ll ans=0;
ll now=0;
for(int i=0;i<(1<<len-1);i++){
now=0;
for(int j=0;j<len;j++){
now=now*10+s[j]-'0';
if(j==len-1||(1<<j)&i){
ans+=now;
now=0;
}
}
}
cout<<ans<<'\n';
return 0;
}
D - communication network Gym - 102890D
meaning of the title
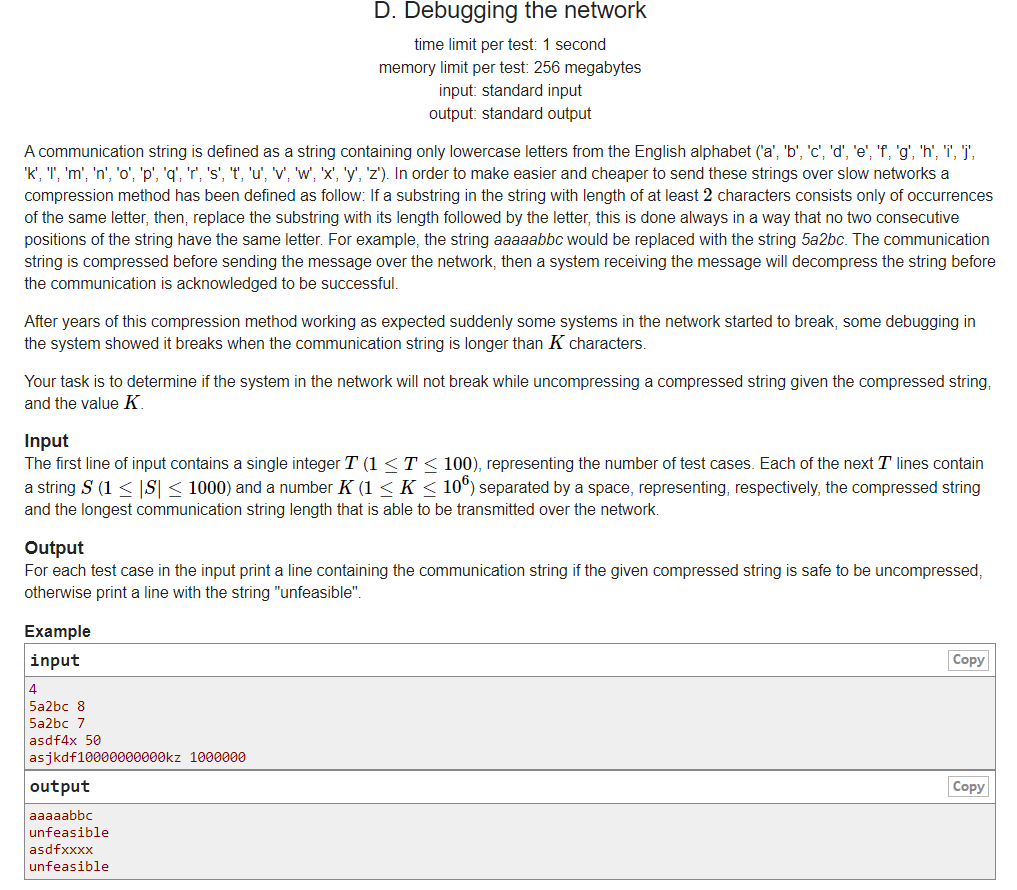
It is required to translate the string and give a maximum length. Exceeding this length is illegal.
As for the string format, the number plus letter indicates how many letters there are. There are only lowercase letters, and numbers can be omitted when there is one.
Problem solution
There's nothing to say. Just simulate.
code
using namespace std;
const int N=1e5;
const ll mod=1000000007;
int a[N];
int main()
{
//IOS
int t;cin>>t;
while(t--){
string s;cin>>s;
int maxn;cin>>maxn;
string ans;
int len=s.length();
int p=1;
bool yes=1;
ll all=0;
for(int i=0;i<len;){
if(s[i]>='a'&&s[i]<='z'){
ans+=s[i];
all++;
i++;
}
else {
int j=i;
string temp;
temp+=s[j++];
while(s[j]>='0'&&s[j]<='9')temp+=s[j],j++;
ll o=atoi(temp.c_str());
all+=o;
if(all>maxn){yes=0;break;}
while(o--)ans+=s[j];
i=j+1;
}
if(yes==0)break;
}
if(all>maxn||(s[len-1]>='0'&&s[len-1]<='9'))yes=0;
if(yes==0)cout<<"unfeasible\n";
else if(yes==1)cout<<ans<<'\n';
}
return 0;
}
E - calculate word Gym - 102890L
meaning of the title
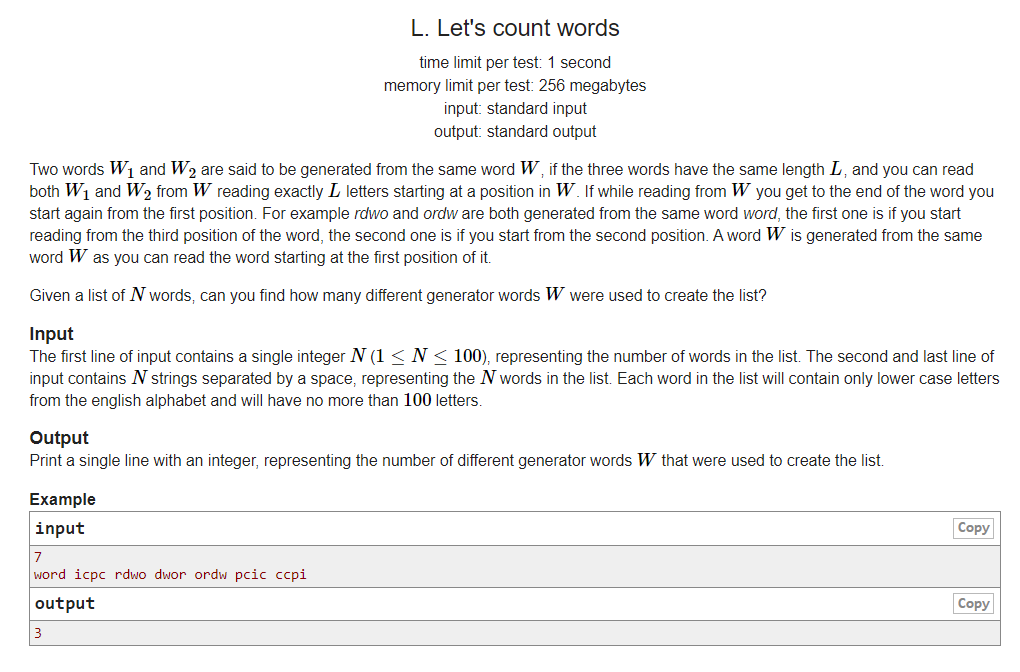
A rule of "substring" and "parent string" is given, that is, the "substring" is the substring after the infinite cycle of "parent string". Now give n strings and find different "number of parent strings".
Problem solution
When judging the attribution relationship, the parent string can be spliced on both sides. First let the answer to n (as each string is irrelevant), traverse each string, compare it with the following string, find one that can be its parent string, subtract 1 from the answer (this string is not passed by the parent, so subtract), and end the matching (because finding it is enough).
code
using namespace std;
const int N=122;
const ll mod=1000000007;
pair<string,string>all[N];
int yes[N];
int main()
{
//IOS
int n;cin>>n;
for(int i=1;i<=n;i++){
string t;cin>>t;
string tt;tt=t+t+t;
all[i]=make_pair(t,tt);
}
ll ans=n;
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
if(all[j].first.length()==all[i].first.length()&&all[j].second.find(all[i].first)!=string::npos){
ans--;
break;
}
}
}
cout<<ans<<'\n';
return 0;
}
G - contestant Gym - 102890K
meaning of the title
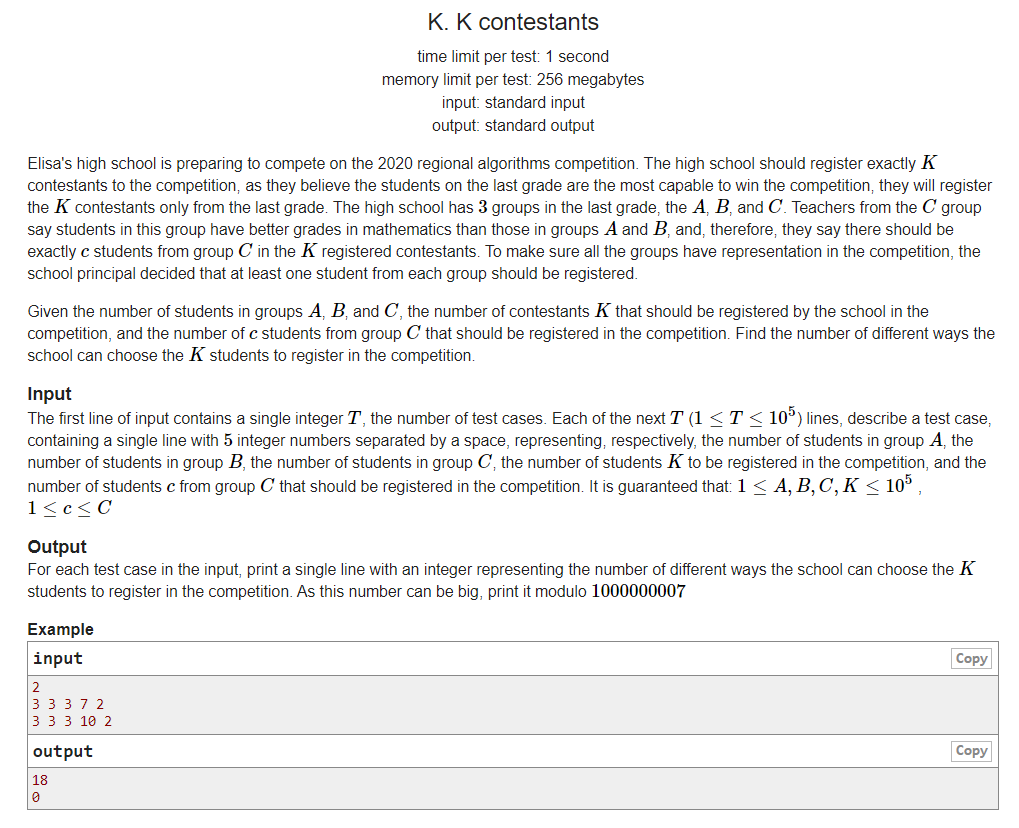
Each of the three groups of ABC has a certain number of people. A total of k people are selected. C must choose C people, and AB must choose at least one person. Find the number of options. Results the model of 1e7 was taken.
Problem solution
The topic turns to the number of schemes in which C individuals are selected from C, K-c individuals are selected from A and B, and at least one person is selected from A and B. Consider the direct combination number calculation, and then subtract the number of schemes in which A chooses K-c and B chooses K-c. (if you can't choose one person without A or b)
Pay attention to judge the rationality first. (there are less than two people left after choosing c)
This problem is difficult in the combination of numbers, because the result needs to be modular. If you divide by 0 according to the method of division, there may be a case. So we need to change it.
There are many ways to find combinatorial numbers, You can see here.
Because there are multiple groups, preprocess first.
code
using namespace std;
const int N=2e5+2;
const ll mod=1000000007;
ll jie[N];
ll tow[N];
ll power(ll a,ll b,ll p) //return a^b mod p
{
ll temp = 1;
while(b)
{
if(b & 0x01)
{
temp = (temp * (a%p)) % p;
}
a = ( (a%p) * (a%p) ) % p;
b >>= 1;
}
return temp%p;
}
void init()
{
jie[0]=1;
for(int i=1;i<N;i++)jie[i]=jie[i-1]*i%mod;
tow[N-1]=power(jie[N-1],mod-2,mod);
for(int i=N-2;i>=0;i--) tow[i]=tow[i+1]*(i+1)%mod;
}
ll cal(ll n,ll m)
{
if(m>n) return 0;
return jie[n]*tow[m]%mod*tow[n-m]%mod;
}
int main()
{
//IOS
init();
int t;cin>>t;
while(t--){
ll A,B,C,k,c;
ll ans=0;
cin>>A>>B>>C>>k>>c;
if(k-c<2){cout<<0<<'\n';continue;}
ll p=k-c;
ll o=cal(A,p)+cal(B,p);o%=mod;
ans=cal(A+B,p)-o+mod;
ans%=mod;
ans*=cal(C,c);
ans%=mod;
cout<<ans<<'\n';
}
return 0;
}
The following questions are not read. They are all difficult questions (there are also naked questions). If you don't read them, you won't write them.