In depth understanding of the sequence before, during and after

In previous binary tree articles, some readers always leave a message saying that they can't see whether the solution should be pre order, middle order or post order. In fact, the reason is that your understanding of pre order, middle order and post order is not in place. Here I'll explain it briefly.

First, let's review Learn the frame thinking of data structure and algorithm The binary tree traversal framework mentioned in:

void traverse(TreeNode root) {
    if (root == null) {
        return;
    }
    // Preamble position
    traverse(root.left);
    // Middle sequence position
    traverse(root.right);
    // Post sequence position
}

Regardless of the so-called first, middle and last order, just look at what this code is?

In fact, it is a function that can traverse all nodes of a binary tree. It is essentially no different from traversing an array or linked list:

/* Iterative traversal array */
void traverse(int[] arr) {
    for (int i = 0; i < arr.length; i++) {

    }
}

/* Recursive traversal array */
void traverse(int[] arr, int i) {
    if (i == arr.length) {
        return;
    }
    // Preamble position
    traverse(arr, i + 1);
    // Post sequence position
}

/* Iterative traversal of single linked list */
void traverse(ListNode head) {
    for (ListNode p = head; p != null; p = p.next) {

    }
}

/* Recursive traversal of single linked list */
void traverse(ListNode head) {
    if (head == null) {
        return;
    }
    // Preamble position
    traverse(head.next);
    // Post sequence position
}

The traversal of single linked list and array can be iterative or recursive. The structure of binary tree is nothing more than binary linked list, but it can not be simply rewritten into iterative form. Therefore, generally speaking, the traversal framework of binary tree refers to recursive form.

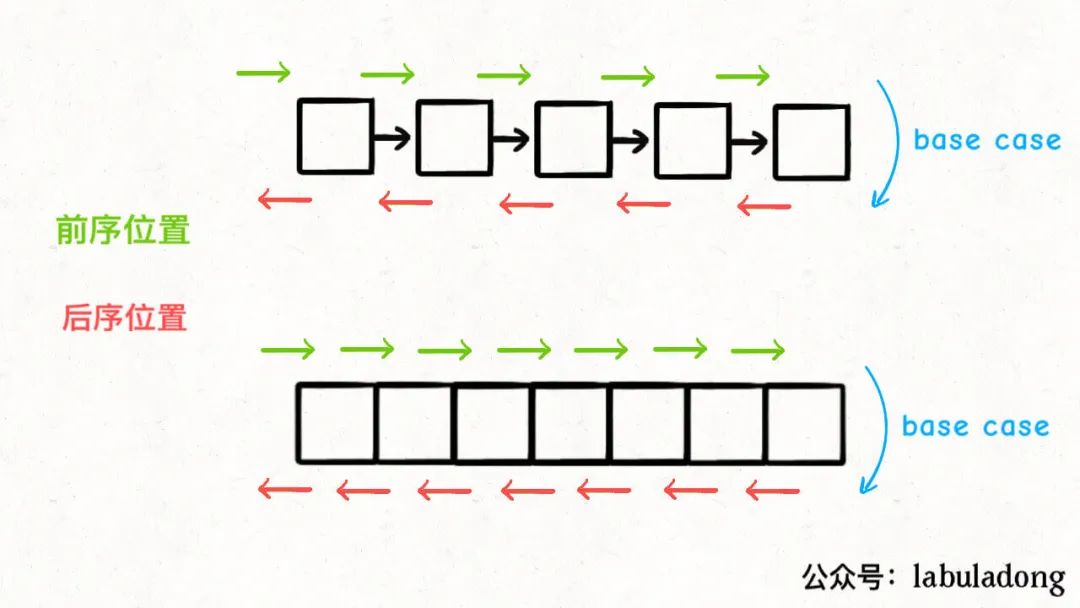
You have also noticed that as long as it is a recursive traversal, there will be a pre order position and a post order position before and after the recursion.

The so-called pre order position is when you first enter a node (element), and the post order position is when you are about to leave a node (element).

When you write code in different places, the timing of code execution is different:

For example, if you are asked to print the values of all nodes in a single linked list in reverse order, what do you do?

Of course, there are many implementation methods, but if you have a thorough understanding of recursion, you can use the post order position:

/* Recursively traverse the single linked list and print the linked list elements in reverse order */
void traverse(ListNode head) {
    if (head == null) {
        return;
    }
    traverse(head.next);
    // Post sequence position
    print(head.val);
}

Combined with the above figure, you should know why this code can print the single linked list in reverse order. In essence, it uses the recursive stack to help you realize the effect of reverse traversal.

So it's the same to say back to the binary tree, just one more middle order position.

Here I emphasize a mistake that beginners often make: because textbooks only ask you what the traversal results of the first, middle and last sequences are respectively, for a person who has only taken a college data structure course, he probably thinks that the first, middle and last sequences of a binary tree only correspond to three list < integer > lists with different orders.

However, I would like to say that the first, middle and last order are three special time points for processing each node in the process of traversing the binary tree, not just three lists with different orders:

The code of the preamble position is executed when it just enters a binary tree node;

The code of the post order position is executed when it is about to leave a binary tree node;

The code of the middle order position is executed when the left subtree of a binary tree node is traversed and the right subtree is about to be traversed.

Pay attention to the words used in this article. I always say that the "position" of the first, middle and last order is different from the "traversal" of the first, middle and last order: you can write code in the position of the first order and insert elements into a List, then you can finally get the result of the traversal of the first order; But that doesn't mean you can't write more complex code and do more complex things.

The first, middle and last three positions in the binary tree are as follows:

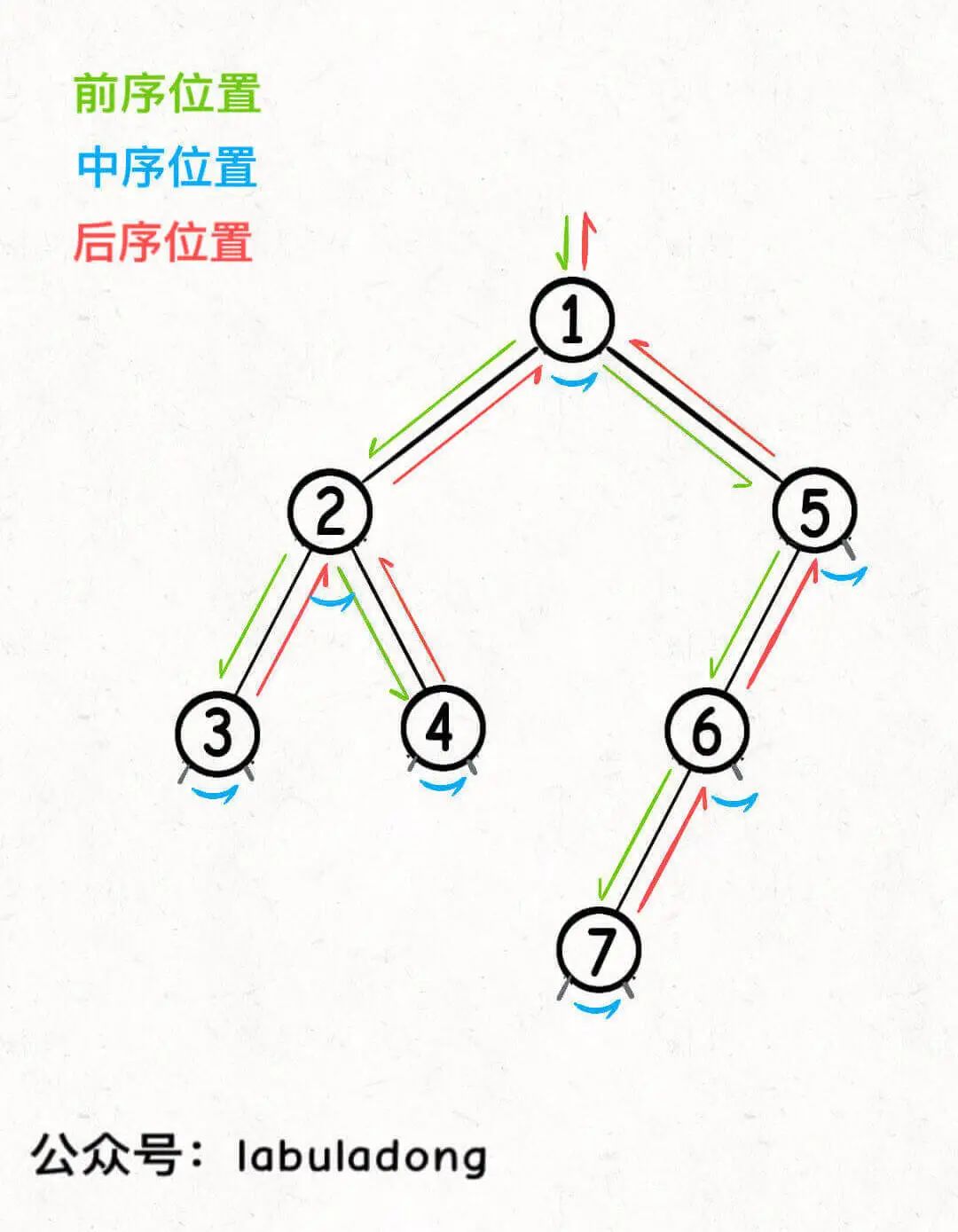
You can find that each node has its own "unique" pre, middle and post order position, so I say that the pre, middle and post order traversal is to process each node at three special time points in the process of traversing the binary tree.

Here you can also understand why the multi tree does not have a middle order position, because each node of the binary tree will only switch the left subtree to the right subtree once, and the multi tree node may have many sub nodes, which will switch the subtree to traverse many times, so the multi tree node does not have a "unique" middle order traversal position.

Having said so many basic things is to help you establish a correct understanding of the binary tree, and then you will find that all the problems of the binary tree are to let you inject clever code logic into the front, middle and back order positions to achieve your own purpose.

This is the core idea of the previous six hand-in-hand brush binary tree articles: you just need to think about what each node should do, and don't worry about the others. Throw it to the binary tree traversal framework, and recursion will do the same operation for all nodes.

As you can see, Fundamentals of graph theory algorithm The traversal framework of binary tree is extended to graph, and various classical algorithms of graph theory are realized based on traversal. However, this is a later topic, which will not be discussed in this paper.

Two ways to solve problems

Above My algorithm learning experience As said, the recursive solution of binary tree problems can be divided into two kinds of ideas. The first kind is to traverse the binary tree to get the answer, and the second kind is to calculate the answer by decomposing the problem. These two kinds of ideas correspond to Core framework of backtracking algorithm and Dynamic programming core framework.

At that time, I used the problem of maximum depth of binary tree as an example, focusing on comparing these two ideas with dynamic programming and backtracking algorithms, and the focus of this paper is to analyze how these two ideas solve the problem of binary tree.

Li Kou's question 104 "maximum depth of binary tree" is the question of maximum depth. The so-called maximum depth is the number of nodes on the longest path from the root node to the "farthest" leaf node. For example, if you enter this binary tree, the algorithm should return 3:

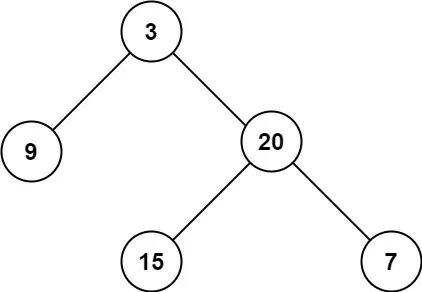
What's your idea for this question? Obviously, traverse the binary tree, record the depth of each node with an external variable, and take the maximum value to get the maximum depth. This is the idea of traversing the binary tree to calculate the answer.

The solution code is as follows:

// Record maximum depth
int res = 0;
// Record the depth of the node traversed
int depth = 0;

// Main function
int maxDepth(TreeNode root) {
    traverse(root);
    return res;
}

// Binary tree traversal framework
void traverse(TreeNode root) {
    if (root == null) {
        // Reach the leaf node and update the maximum depth
        res = Math.max(res, depth);
        return;
    }
    // Preamble position
    depth++;
    traverse(root.left);
    traverse(root.right);
    // Post sequence position
    depth--;
}

This solution should be well understood, but why do you need to increase depth in the pre order position and decrease depth in the post order position?

As mentioned earlier, the pre order position is when entering a node, and the post order position is when leaving a node. Depth records the current recursive node depth, so it should be maintained in this way.

Of course, you can easily find that the maximum depth of a binary tree can be derived from the maximum height of the subtree, which is the idea of decomposing the problem and calculating the answer.

The solution code is as follows:

// Definition: enter the root node and return the maximum depth of the binary tree
int maxDepth(TreeNode root) {
    if (root == null) {
        return 0;
    }
    // Using the definition, calculate the maximum depth of the left and right subtrees
    int leftMax = maxDepth(root.left);
    int rightMax = maxDepth(root.right);
    // The maximum depth of the whole tree is equal to the maximum depth of the left and right subtrees, and the maximum value is taken,
    // Then add the root node itself
    int res = Math.max(leftMax, rightMax) + 1;

    return res;
}

As long as the definition of recursive function is clear, this solution is not difficult to understand, but why do the main code logic focus on the post order position?

Because the correct core of this idea is that you can really deduce the height of the original tree from the maximum height of the subtree, so of course, you should first calculate the maximum depth of the left and right subtrees by using the definition of the recursive function, and then deduce the maximum depth of the original tree. The main logic is naturally placed in the subsequent position.

If you understand the two ideas of the maximum depth problem, let's go back to the most basic binary tree preorder traversal, such as calculating the preorder traversal result.

The solution we are familiar with is to use the idea of "traversal". I think there should be nothing to say:

List<Integer> res = new LinkedList<>();

// Return preorder traversal result
List<Integer> preorderTraverse(TreeNode root) {
    traverse(root);
    return res;
}

// Binary tree traversal function
void traverse(TreeNode root) {
    if (root == null) {
        return;
    }
    // Preamble position
    res.add(root.val);
    traverse(root.left);
    traverse(root.right);
}

But can you use the idea of "decomposing the problem" to calculate the result of preorder traversal?

In other words, don't use auxiliary functions like traverse and any external variables. Just use the preorderTraverse function given by the topic to solve the problem recursively. Will you?

We know that the characteristic of preorder traversal is that the value of the root node ranks first, followed by the preorder traversal result of the left subtree, and finally the preorder traversal result of the right subtree:

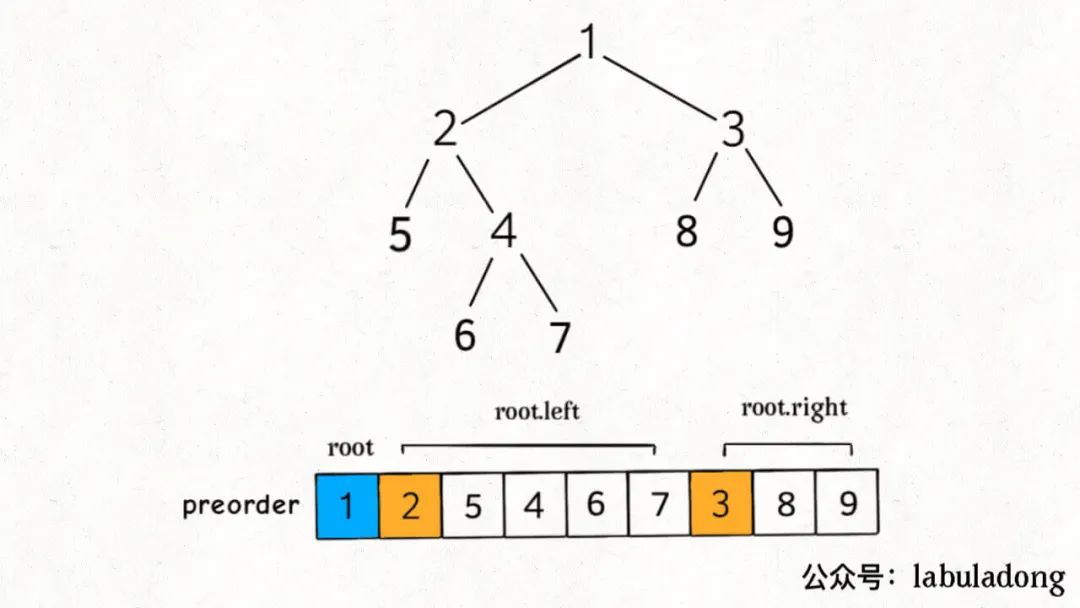
Then this can decompose the problem. The preorder traversal of a binary tree is decomposed into the preorder traversal results of the root node and the left and right subtrees.

Therefore, you can implement the preorder traversal algorithm as follows:

// Definition: enter the root node of a binary tree and return the preorder traversal result of the tree
List<Integer> preorderTraverse(TreeNode root) {
    List<Integer> res = new LinkedList<>();
    if (root == null) {
        return res;
    }
    // The result of preorder traversal, root Val in the first
    res.add(root.val);
    // Using the function definition, followed by the preorder traversal result of the left subtree
    res.addAll(preorderTraverse(root.left));
    // Using the function definition, and then the preorder traversal result of the right subtree
    res.addAll(preorderTraverse(root.right));
}

Middle order and post order traversal are similar. Just put add(root.val) in the corresponding position of middle order and post order.

This solution is short and capable, but why is it not common?

One reason is that the complexity of this algorithm is not easy to control, and it depends on language characteristics.

In Java, no matter ArrayList or LinkedList, the complexity of addAll method is O(N), so the overall worst-case time complexity will reach O(N^2). Unless you implement an addAll method with complexity of O(1), it is not impossible to use a linked list at the bottom.

Of course, the main reason is that it has never been taught in Textbooks

Two simple examples are given above, but there are many binary tree problems that can be thought and solved by using two ideas at the same time. It depends on you to practice and think more. Don't just be satisfied with a familiar solution idea.

To sum up, the general thinking process when encountering a binary tree is:

Can I get the answer by traversing the binary tree? If not, can a recursive function be defined to deduce the answer of the original question from the answer of the sub question (sub tree)?

My question brushing plug-in All the binary tree topics worth doing have been updated and classified into the above two ideas. If you solve all the binary tree topics according to the ideas provided by the plug-in, you can not only fully master the recursive thinking, but also more easily understand the advanced algorithm:

Special features of post sequence position

Before talking about the post order position, briefly talk about the next middle order and the pre order.

The middle order position is mainly used in the BST scenario. You can think of the middle order traversal of BST as traversing an ordered array.

In fact, the preamble position itself has no special nature. The reason why you find that many questions seem to write code in the preamble position is actually because we are used to writing code that is not sensitive to the preamble position.

Next, we will mainly talk about the next sequence position. Compared with the previous sequence position, it is found that the code execution of the previous sequence position is top-down, and the code execution of the latter sequence position is bottom-up:

This is not surprising, because it was said at the beginning of this article that the pre order position is the moment when the node has just entered, and the post order position is the moment when the node is about to leave.

However, there is a mystery in this, which means that the code at the pre order position can only obtain the data passed by the parent node from the function parameters, and the code at the post order position can not only obtain the parameter data, but also obtain the data passed back by the sub tree through the function return value.

Let me give you a specific example. Now I'll give you a binary tree. I'll ask you two simple questions:

1. If the root node is regarded as the first layer, how to print the number of layers of each node?

2. How to print out the number of nodes in the left and right subtrees of each node?

The first question can be written as follows:

// Binary tree traversal function
void traverse(TreeNode root, int level) {
    if (root == null) {
        return;
    }
    // Preamble position
    printf("node %s In the first %d layer", root, level);
    traverse(root.left, level + 1);
    traverse(root.right, level + 1);
}

// Call like this
traverse(root, 1);

The second question can be written as follows:

// Definition: enter a binary tree and return the total number of nodes of the binary tree
int count(TreeNode root) {
    if (root == null) {
        return 0;
    }
    int leftCount = count(root.left);
    int rightCount = count(root.right);
    // Post sequence position
    printf("node %s The left subtree of has %d Nodes, right subtree %d Nodes",
            root, leftCount, rightCount);

    return leftCount + rightCount + 1;
}

Combining these two simple questions, you can taste the characteristics of the post order position. Only the post order position can obtain the information of the subtree through the return value.

In other words, once you find that the problem is related to the subtree, you have to set a reasonable definition and return value for the function and write code in the subsequent position.

Next, let's look at how the sequential position plays a role in the actual problem. Let's talk about question 543 "diameter of binary tree" and let you calculate the longest "diameter" length of a binary tree.

The "diameter" length of a binary tree is the path length between any two nodes. The longest "diameter" does not necessarily pass through the root node, such as the following binary tree:

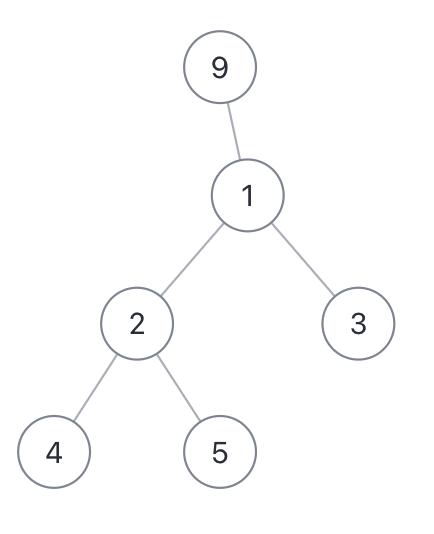
Its diameter is 3, that is, the length of the two paths [4,2,1,3] or [5,2,1,3].

The key to solve this problem is that the "diameter" length of each binary tree is the sum of the maximum depths of the left and right subtrees of a node.

Now let me find the longest "diameter" in the whole tree. The straightforward idea is to traverse each node in the whole tree, then calculate the "diameter" of each node through the maximum depth of the left and right subtrees of each node, and finally find the maximum value of all "diameters".

We have just implemented the maximum depth algorithm. The above idea can write the following code:

// Record the length of the maximum diameter
int maxDiameter = 0;

public int diameterOfBinaryTree(TreeNode root) {
    // Calculate the diameter of each node and find the maximum diameter
    traverse(root);
    return maxDiameter;
}

// Traversal binary tree
void traverse(TreeNode root) {
    if (root == null) {
        return;
    }
    // Calculate the diameter for each node
    int leftMax = maxDepth(root.left);
    int rightMax = maxDepth(root.right);
    int myDiameter = leftMax + rightMax;
    // Update global maximum diameter
    maxDiameter = Math.max(maxDiameter, myDiameter);

    traverse(root.left);
    traverse(root.right);
}

// Calculate the maximum depth of the binary tree
int maxDepth(TreeNode root) {
    if (root == null) {
        return 0;
    }
    int leftMax = maxDepth(root.left);
    int rightMax = maxDepth(root.right);
    return 1 + Math.max(leftMax, rightMax);
}

This solution is correct, but it takes a long time. The reason is obvious. Traverse will call the recursive function maxDepth when traversing each node, and maxDepth will traverse all subtrees, so the worst time complexity is O(N^2).

This is the case just discussed. The pre order position cannot obtain the subtree information, so each node can only call the maxDepth function to the depth of the operator tree.

How to optimize? We should put the logic of calculating the "diameter" in the post order position, precisely in the post order position of maxDepth, because the post order position of maxDepth knows the maximum depth of the left and right subtrees.

Therefore, a better solution can be obtained by slightly changing the code logic:

// Record the length of the maximum diameter
int maxDiameter = 0;

public int diameterOfBinaryTree(TreeNode root) {
    maxDepth(root);
    return maxDiameter;
}

int maxDepth(TreeNode root) {
    if (root == null) {
        return 0;
    }
    int leftMax = maxDepth(root.left);
    int rightMax = maxDepth(root.right);
    // Calculate the maximum diameter at the subsequent position
    int myDiameter = leftMax + rightMax;
    maxDiameter = Math.max(maxDiameter, myDiameter);

    return 1 + Math.max(leftMax, rightMax);
}

Now the time complexity is only O(N) of maxDepth function.

At this point, refer to the previous article: when you encounter a subtree problem, you first think of setting the return value of the function, and then make an article in the post order position.

Conversely, if you write a recursive solution similar to the one at the beginning, you also need to reflect on whether it can be optimized through post order traversal.

My question brushing plug-in There are also special instructions for this kind of post order traversal problems, and pre topics will be given to help you understand this kind of problems from simple to deep:

level traversal

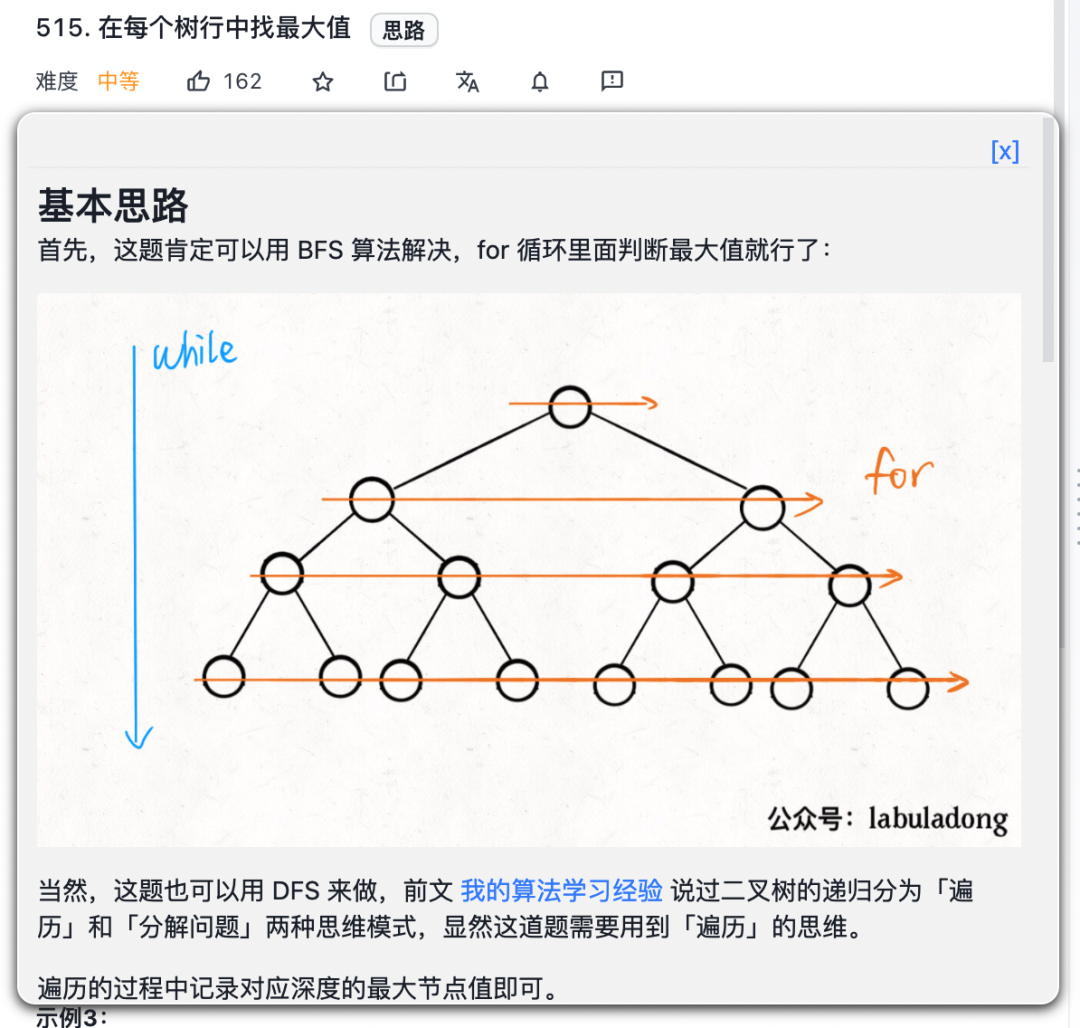
Binary tree questions are mainly used to cultivate recursive thinking, and sequence traversal belongs to iterative traversal, which is also relatively simple. Let's talk about the code framework here:

// Enter the root node of a binary tree and traverse the binary tree
void levelTraverse(TreeNode root) {
    if (root == null) return;
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);

    // Traverse each layer of the binary tree from top to bottom
    while (!q.isEmpty()) {
        int sz = q.size();
        // Traverse each node of each layer from left to right
        for (int i = 0; i < sz; i++) {
            TreeNode cur = q.poll();
            // Put the next level node in the queue
            if (cur.left != null) {
                q.offer(cur.left);
            }
            if (cur.right != null) {
                q.offer(cur.right);
            }
        }
    }
}

The while loop and for loop are responsible for traversal from top to bottom and from left to right:

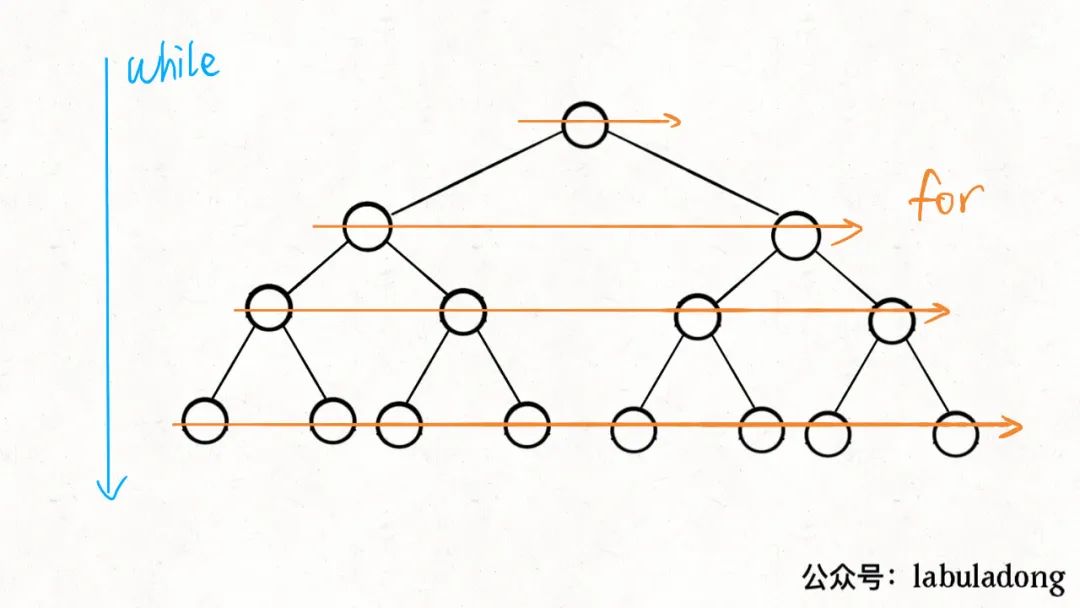
Above BFS algorithm framework It is extended from the sequence traversal of binary tree. It is often used to find the shortest path problem of weighted graph.

Of course, this framework can also be modified flexibly. When the title does not need to record the number of layers (steps), the for loop in the above framework can be removed, such as the above Dijkstra algorithm The shortest path problem of weighted graph is calculated, and the extension of BFS algorithm is discussed in detail.

It is worth mentioning that some binary tree problems that obviously need sequence traversal skills can also be solved by recursive traversal, and the skills will be stronger. It is very important to investigate your control over the front, middle and rear sequences.

For such problems, My question brushing plug-in The solution code of recursive traversal and sequence traversal will also be provided:

Well, this article is long enough. Around the first, middle and last order positions, you have explained all kinds of routines in the binary tree topic. How much you can really use, you need to brush the topic yourself, practice and think about it.

I hope you can explore as many solutions as possible. As long as you understand the principle of the basic data structure of binary tree, it is easy to find a grip on the road of learning other advanced algorithms, open the loop and form a closed loop (manual dog head).