Article Directory
1. Reconstruction of Binary Trees
There is an algorithm problem in LeetCode: Rebuilding Binary Tree.
(1) Interview Question 07. Rebuilding Binary Tree
Interview Question 07. Rebuilding Binary Tree
Enter the results of a binary tree's prefix and median traversals, and rebuild the binary tree.Assume that no duplicate numbers are included in the results of the preceding and middle traversals of the inputs.
For example, given
Pre-order traversal preorder = [3,9,20,15,7] Intermediate traversal inorder = [9,3,15,20,7]
Returns the following binary tree:
3
/ \
9 20
/ \
15 7
Restrictions:
0 <=Number of nodes <= 5000
(2) Analyzing the subject
As you can see from the title, two arrays are given, one is the result of traversing a binary tree in the preamble and the other is the result of traversing a binary tree in the middle order.
Using these two results, a binary tree is restored.
The first thing you need to know is what preceding and middle traversals are.You also need to know how to give you a binary tree and use these traversal algorithms to get the result of traversal, otherwise you will not be able to continue rebuilding the binary tree.
If you haven't entered traversal of binary trees yet, you can read this article:
How can I debug the traversal of a binary tree step by step (great accompaniment)? No more worries about binary tree traversal?
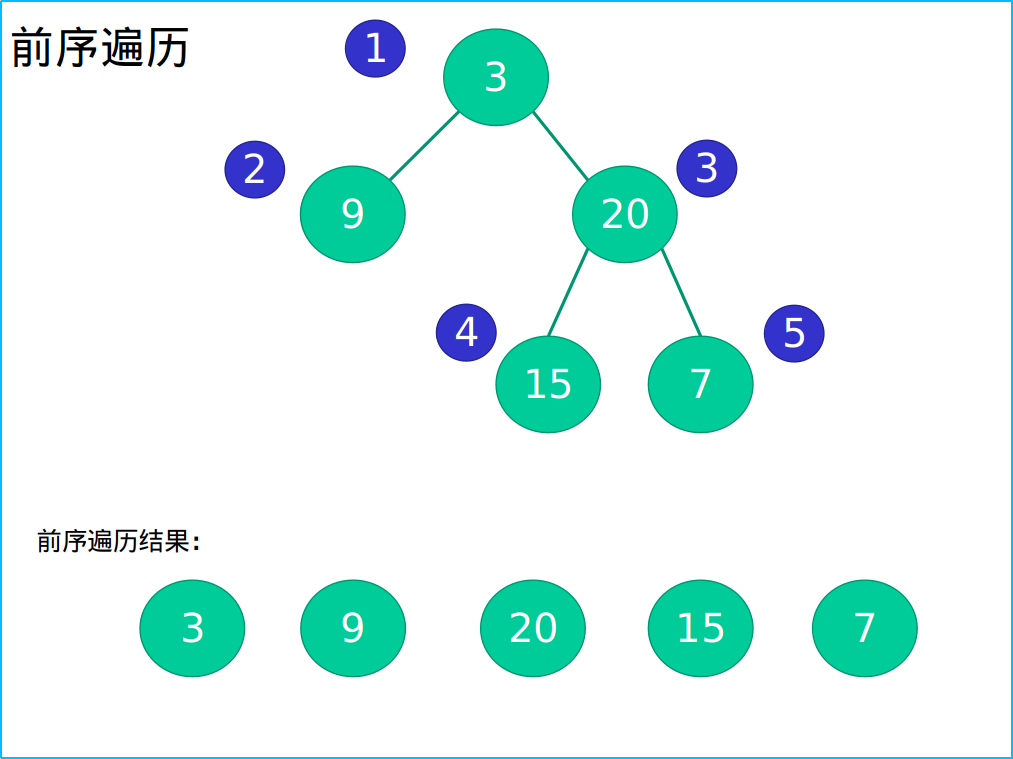
Let's first look at preorder traversal
As shown in the following figure, the prefix traversal is root-left-right
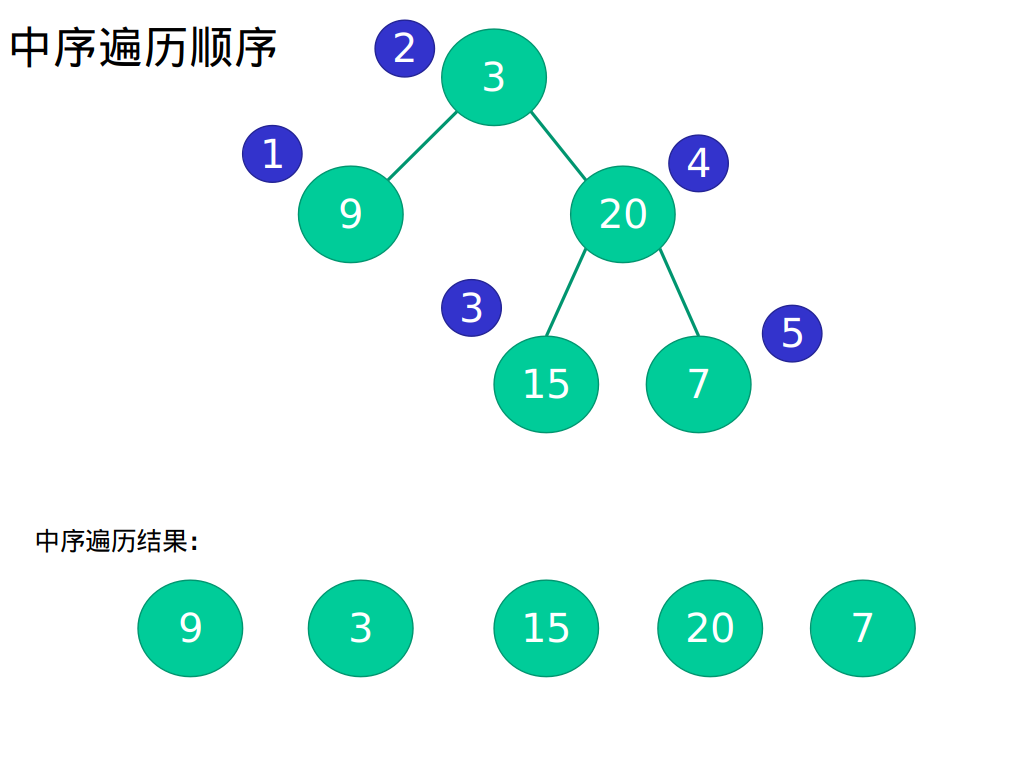
Let's take another look at middle traversal:
The final traversal is left-root-right
The resulting array is:
Pre-order traversal preorder = [3,9,20,15,7] Intermediate traversal inorder = [9,3,15,20,7]
If you are careful, you will find that the first preceding traverse is 3, which is the root node of the whole binary tree.
Look at the results of the middle order:
As shown in the figure below, if we split the left and right parts of the three positions in the middle order, we get all the left and right nodes of root node 3.
[9],[3],[15,20,7]
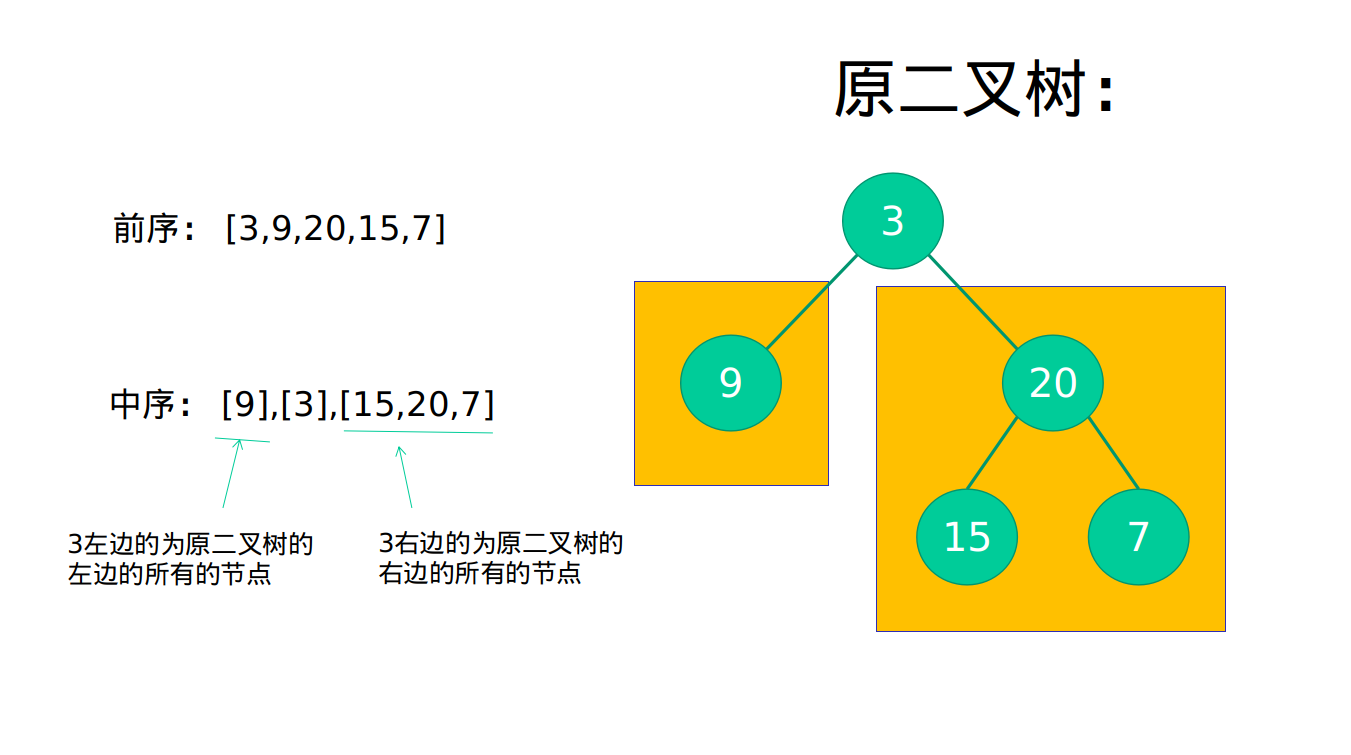
It is not difficult to find that if we use this analogy, we can restore a binary tree.
(3) Implementation of java code
package tree; import java.util.Arrays; /** * @Auther: truedei * @Date: 2020 /20-6-9 12:00 * @Description: Binary Tree Reconstruction */ public class Solution { /** * Building a binary tree from the results of a binary tree traversed in preceding and middle order * @param preorder Array of preceding traversal results * @param inorder Array of intermediate traversal results * @return Return a built binary tree */ static public TreeNode buildTree(int[] preorder, int[] inorder) { if(preorder==null || preorder.length==0) return null; //1, get the value of the root node of the tree TreeNode root = new TreeNode(preorder[0]); //2, find the location of each root node in the middle traversal result int index = findIndex(preorder[0],inorder); //3. Building a left subtree of left // Root.left= buildTree (ordinal array before left subtree, ordinal array in left subtree) root.left = buildTree(Arrays.copyOfRange(preorder,1,index + 1 ), Arrays.copyOfRange(inorder,0,index)); //4. Build a reght right subtree // Root.right=buildTree(Pre-ordinal array of right subtree, ordinal array of right subtree) root.right = buildTree(Arrays.copyOfRange(preorder,index+1,preorder.length), Arrays.copyOfRange(inorder,index+1,inorder.length)); return root; } /** * Function to find root's index (position in middle order) * @param preorderData node * @param inorder Median Array for Each Time * @return Index Location */ static public int findIndex(int preorderData, int[] inorder){ for (int i = 0; i < inorder.length; i++) { if(inorder[i]==preorderData) return i; } return 0; } public static void main(String[] args) { TreeNode treeNode = buildTree(new int[]{3,9,20,15,7}, new int[]{9,3,15,20,7}); theFirstTraversal(treeNode); } //A sequential traversal is used to test if the final result is correct public static void theFirstTraversal(TreeNode root) { System.out.println(root.val); if (root.left != null) { //Traversing the left child using recursion theFirstTraversal(root.left); } if (root.right != null) { //Recursively traverse right child theFirstTraversal(root.right); } } }
Core Code:
Used for recursively building binary trees
/** * Building a binary tree from the results of a binary tree traversed in preceding and middle order * @param preorder Array of preceding traversal results * @param inorder Array of intermediate traversal results * @return Return a built binary tree */ static public TreeNode buildTree(int[] preorder, int[] inorder) { if(preorder==null || preorder.length==0) return null; //1, get the value of the root node of the tree TreeNode root = new TreeNode(preorder[0]); //2, find the location of each root node in the middle traversal result int index = findIndex(preorder[0],inorder); //3. Building a left subtree of left // Root.left= buildTree (ordinal array before left subtree, ordinal array in left subtree) root.left = buildTree(Arrays.copyOfRange(preorder,1,index + 1 ), Arrays.copyOfRange(inorder,0,index)); //4. Build a reght right subtree // Root.right=buildTree(Pre-ordinal array of right subtree, ordinal array of right subtree) root.right = buildTree(Arrays.copyOfRange(preorder,index+1,preorder.length), Arrays.copyOfRange(inorder,index+1,inorder.length)); return root; } /** * Function to find root's index (position in middle order) * @param preorderData node * @param inorder Median Array for Each Time * @return Index Location */ static public int findIndex(int preorderData, int[] inorder){ for (int i = 0; i < inorder.length; i++) { if(inorder[i]==preorderData) return i; } return 0; }
There must be 100,000 reasons why and why to write like this. In fact, there are many ways of writing.Next let's debug it and see what it looks like when it's executed.
(4) Debugging IDEA code and reviewing the process of construction in detail
The tool I use here is IDEA.
To facilitate debugging and to view the results of each execution, we first break points.
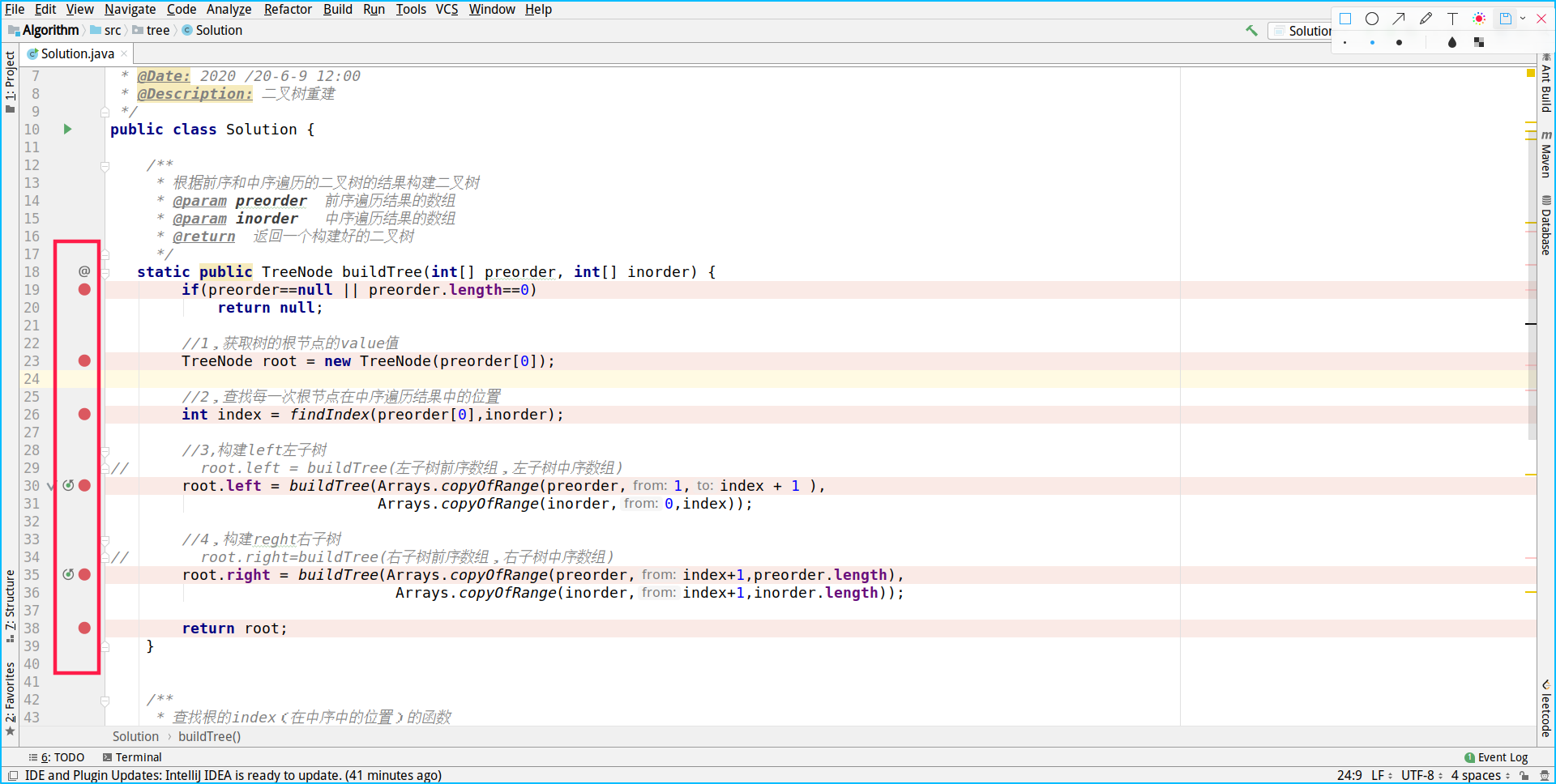
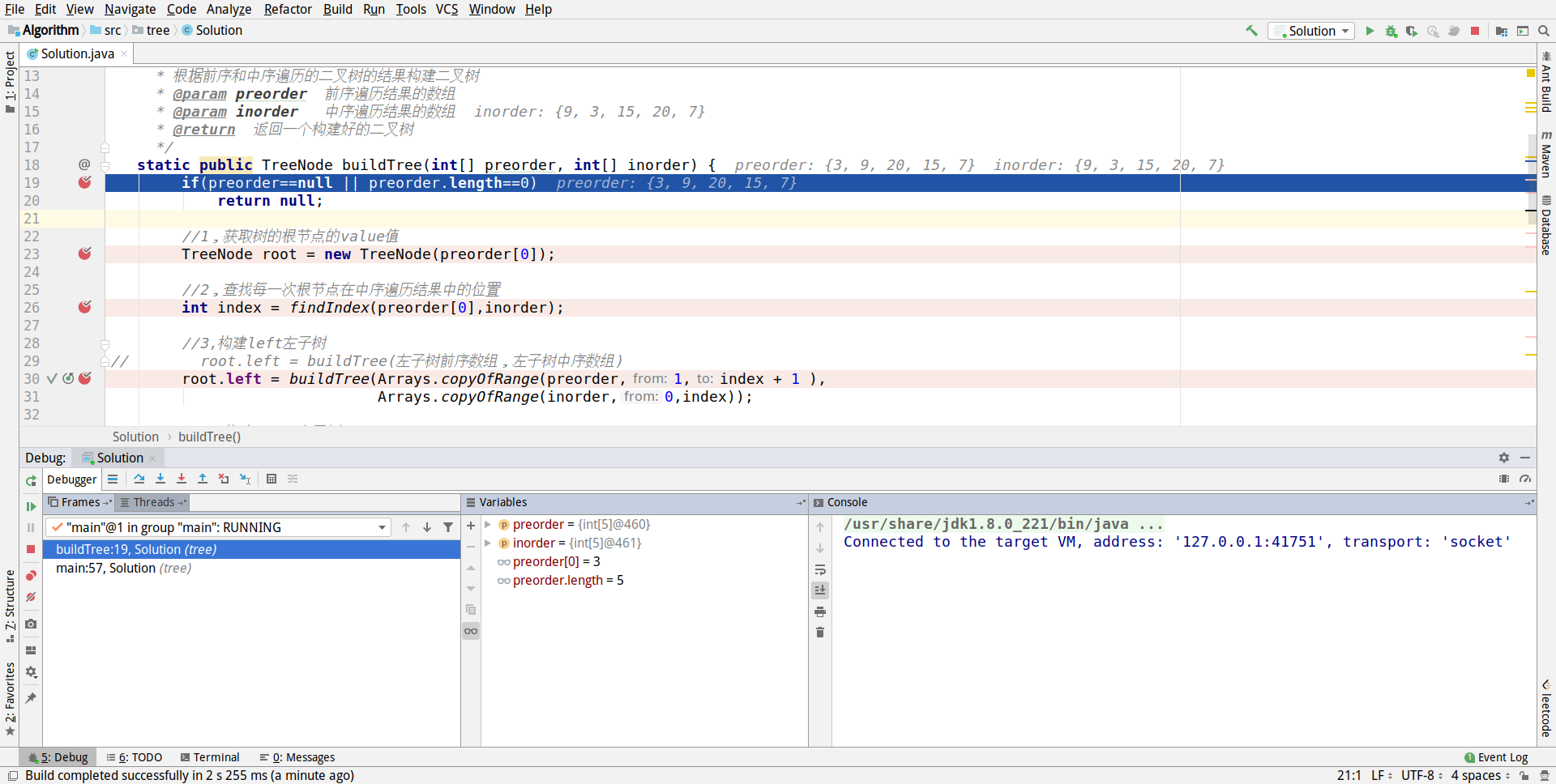
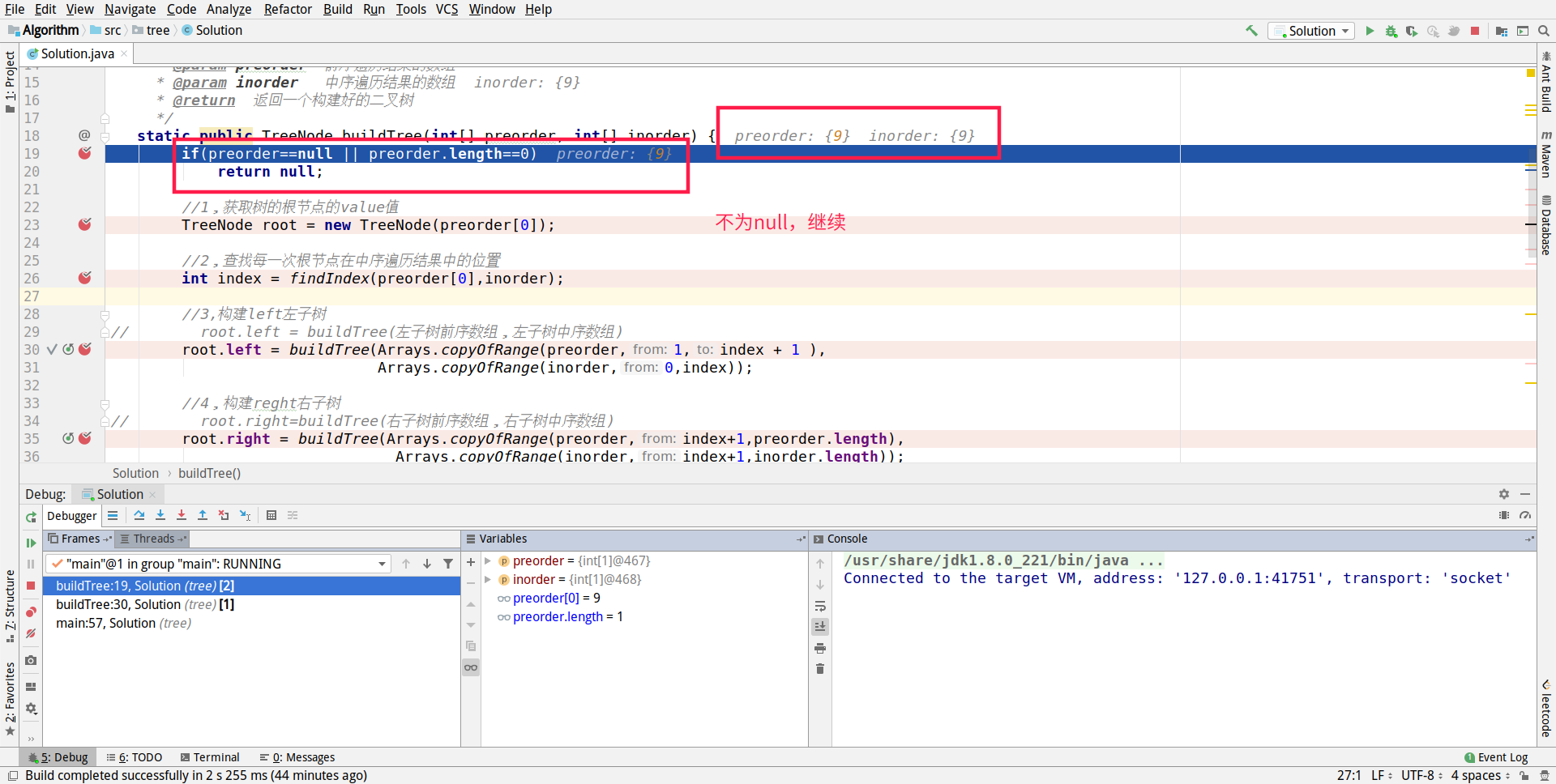
Debug then runs the java file, as shown in the following figure, which is the result of the initial run
Learn more about:
You can see that the preordinal and median ordered arrays passed in now are:
Pre-order traversal preorder = [3,9,20,15,7]
Intermediate traversal inorder = [9,3,15,20,7]
You must be impressed.
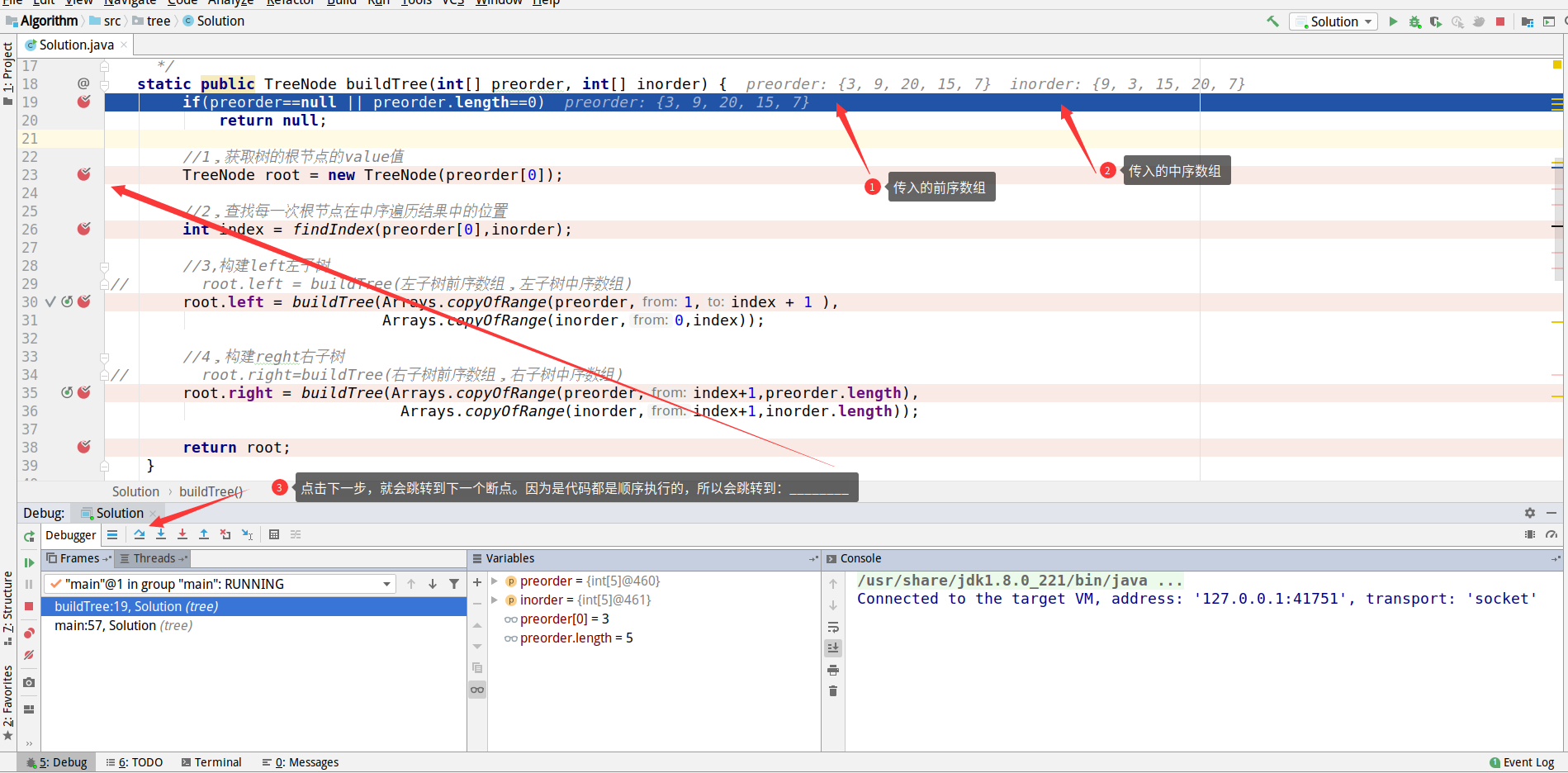
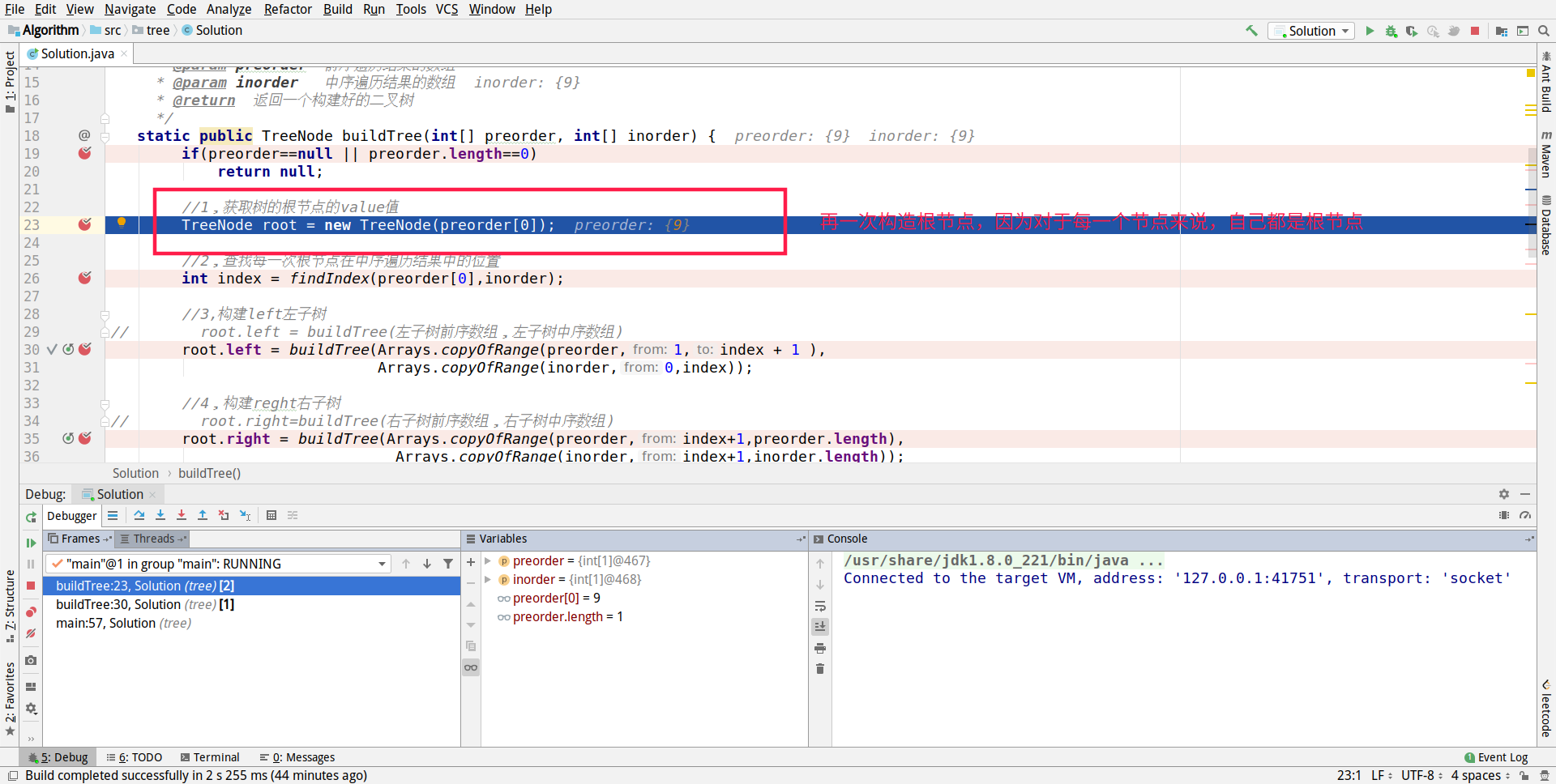
The following is what we see as we move on to the next step in the previous diagram.
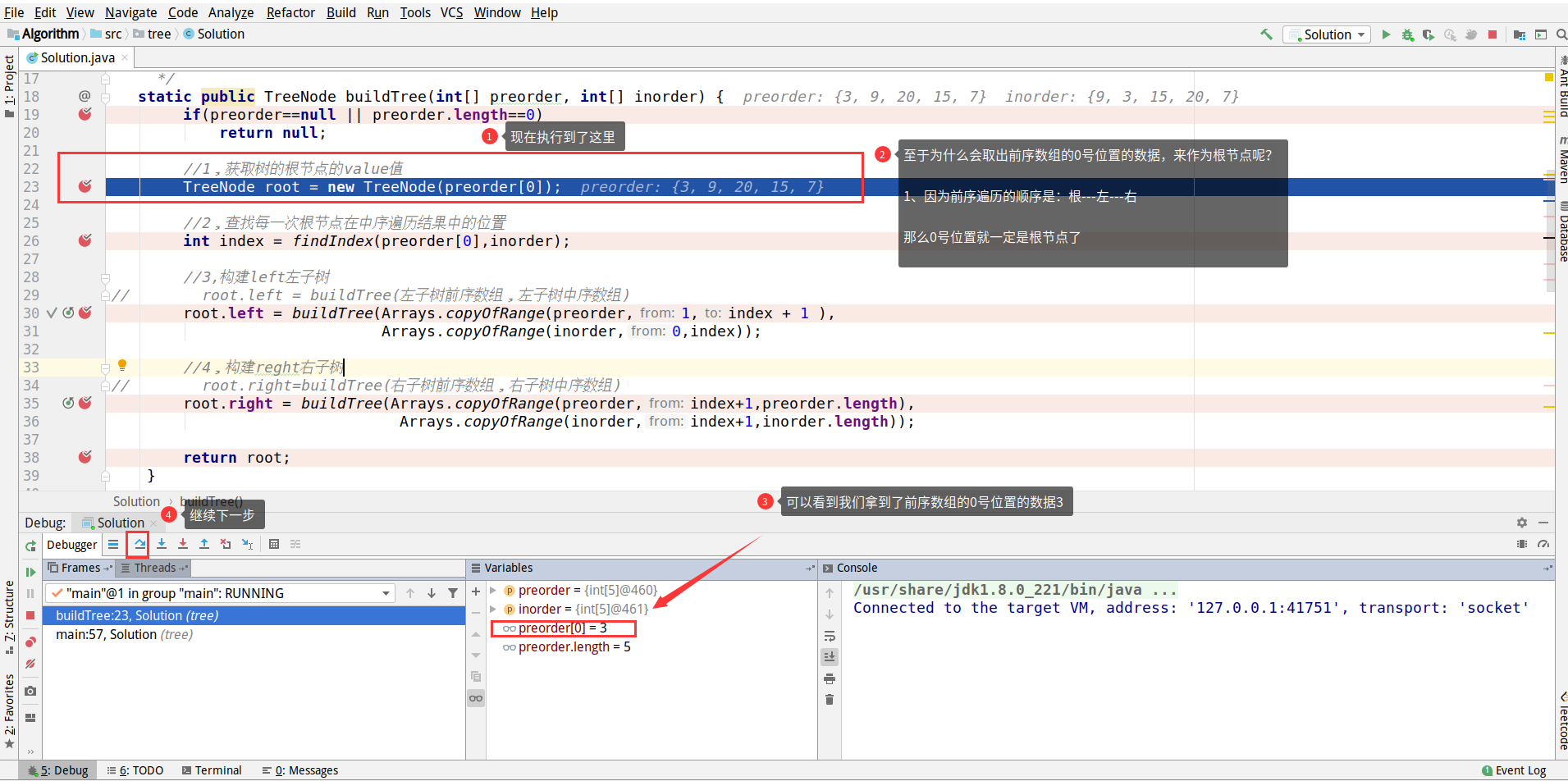
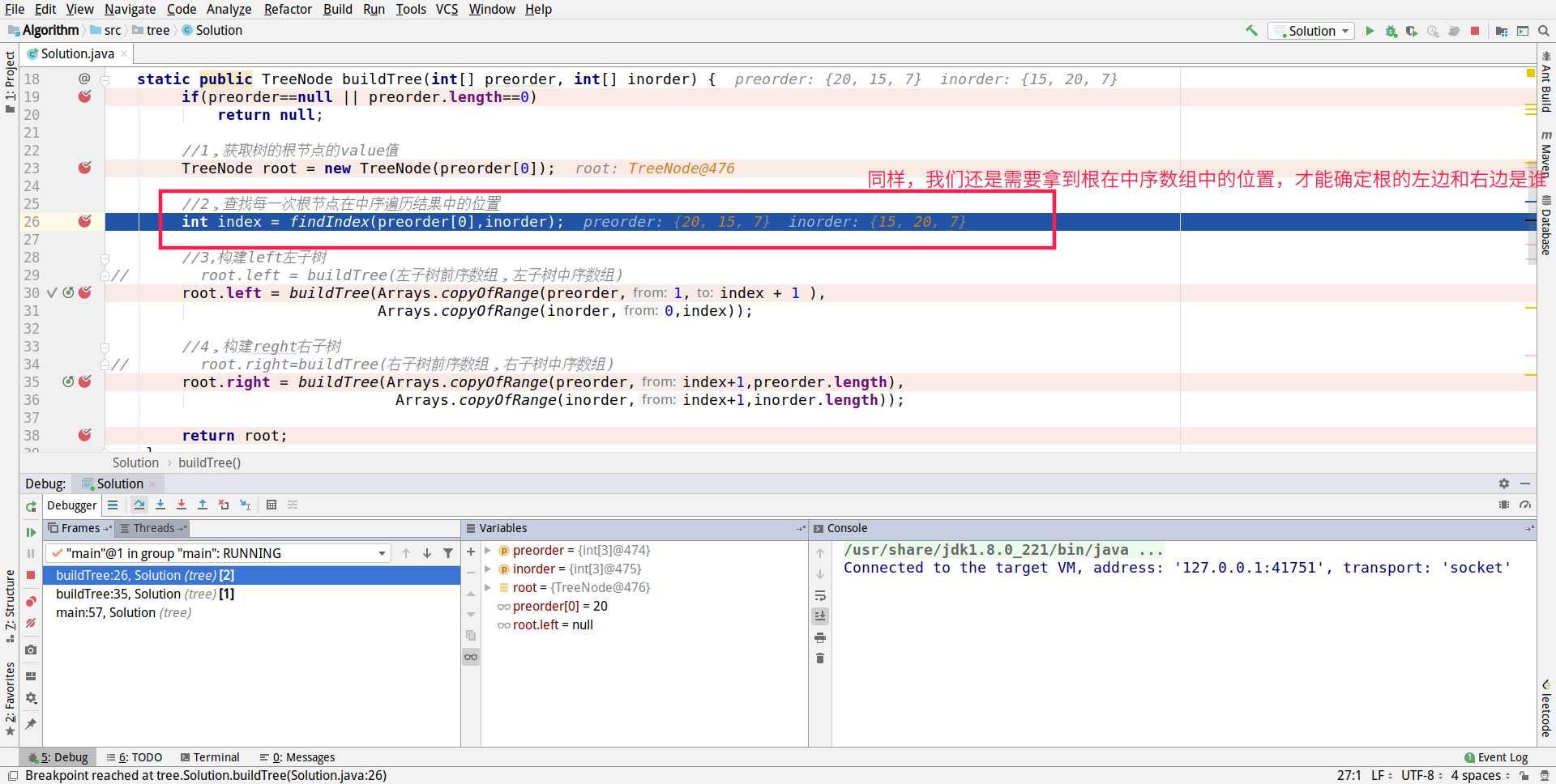
In this operation, we are working on TreeNode root = new TreeNode(preorder[0]);
We've got the data for position 0 of the preceding ordinal array. As to why we have to get the data for position 0 of the preceding ordinal array, see the following figure.The explanation is clear.
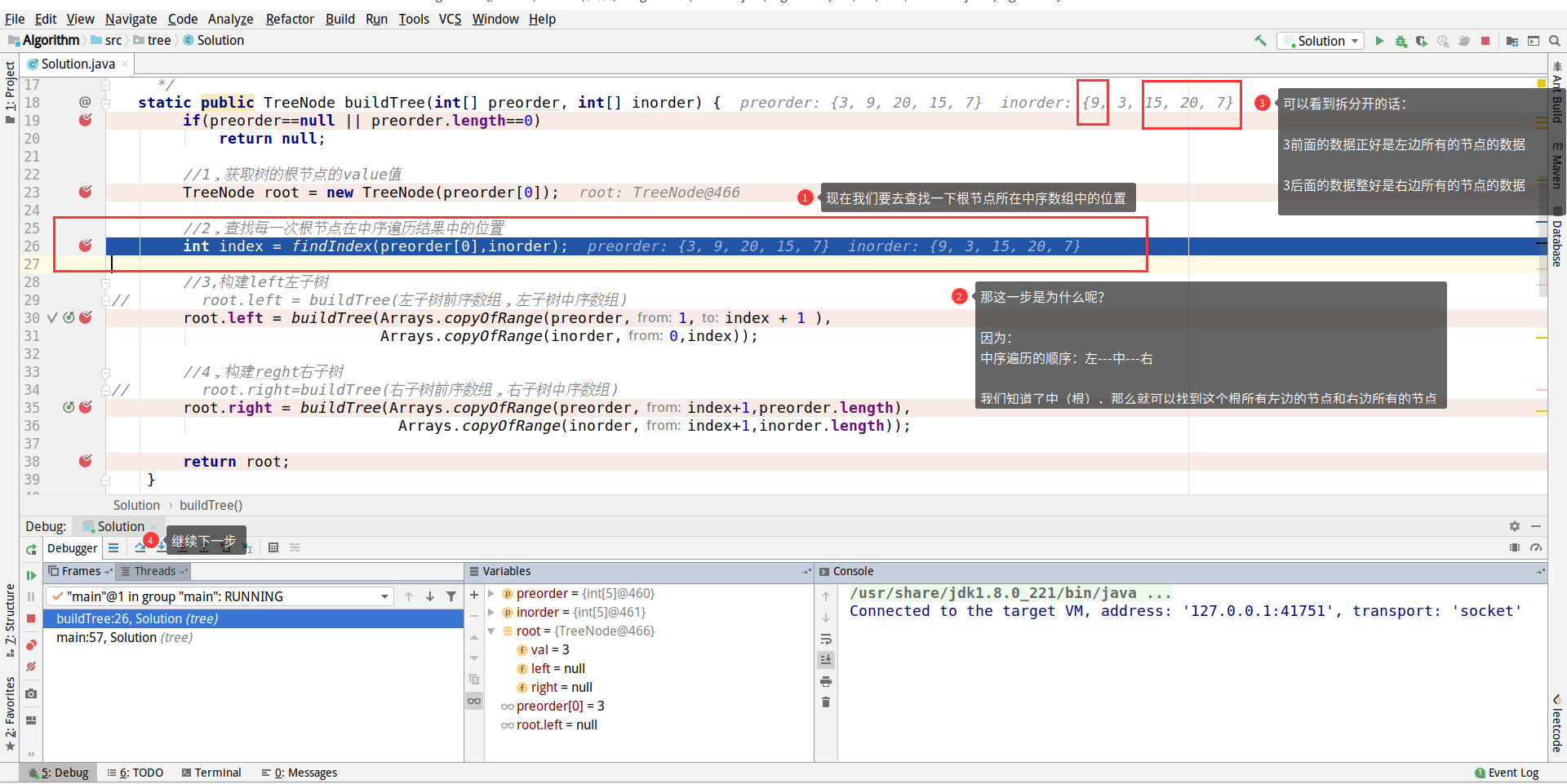
After the next step, you will see the following results;
Here we're going to find the location of the three we got in the middle order array
As to why, see the following picture
Not explained hereArrays.copyOfRange(5) AttachmentArrays.copyOfRangeThe usage of () is ready for everyone.
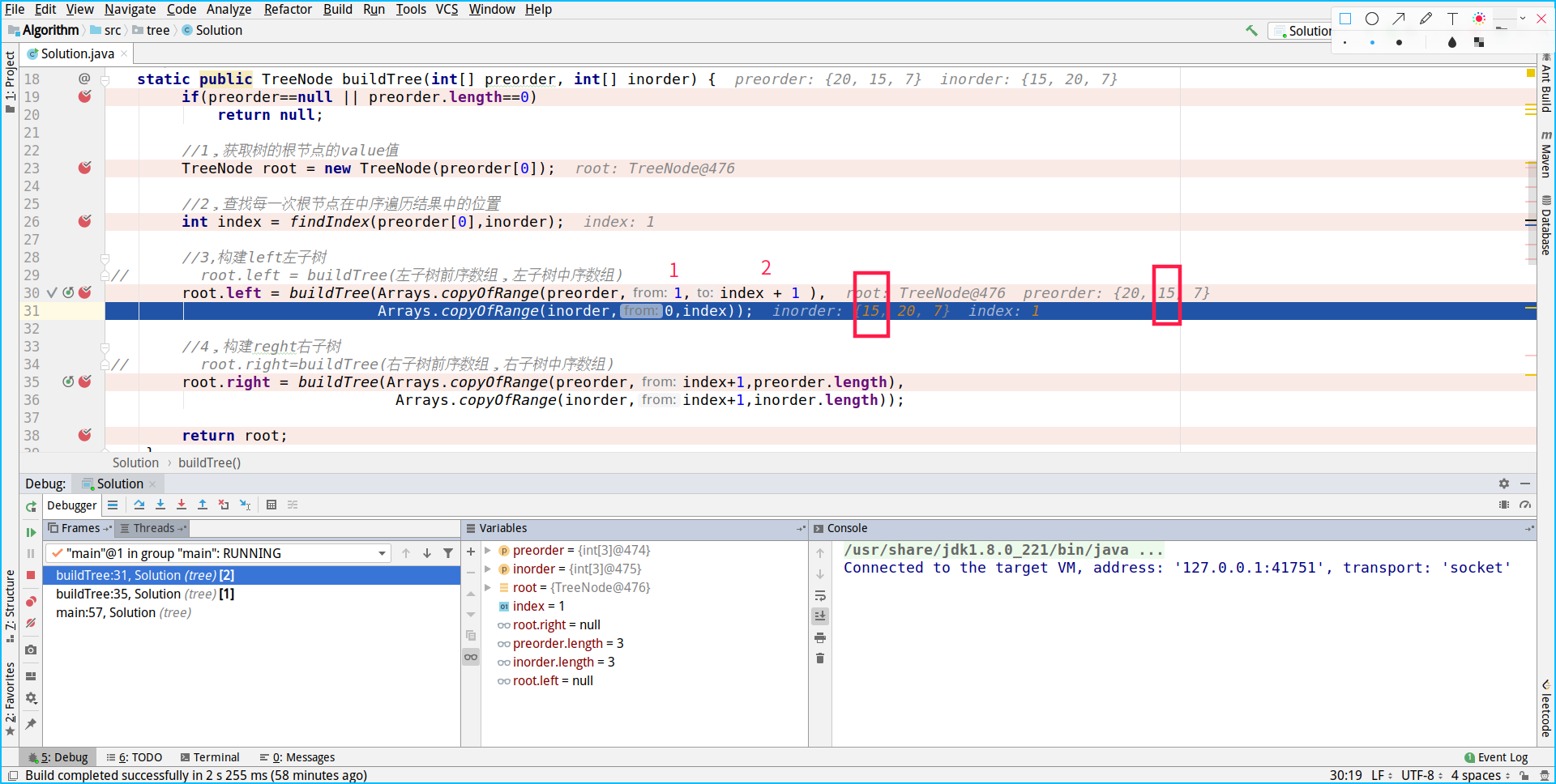
Next, use the index you get to build a left node
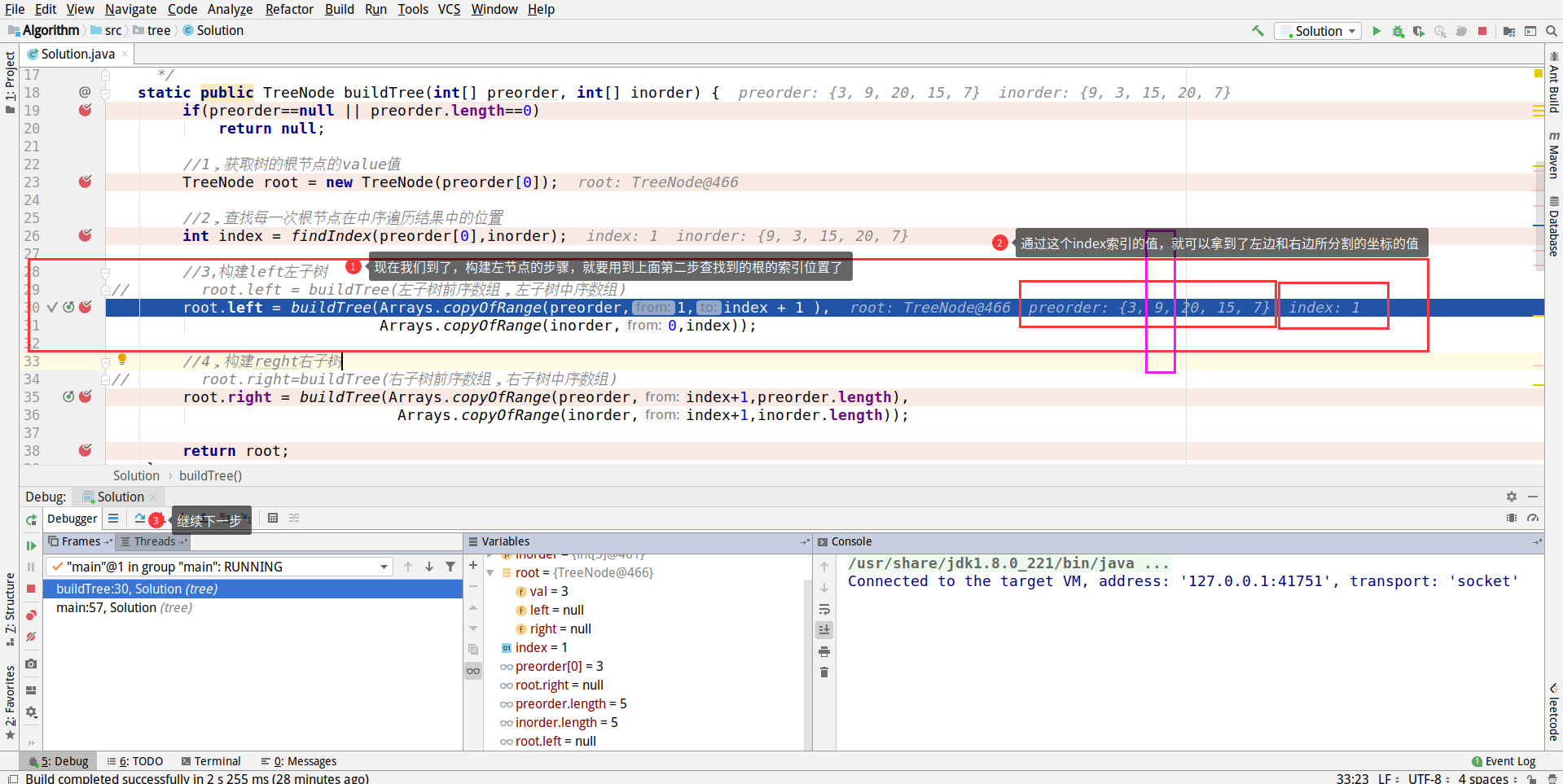
Continue to the next step

Continue to the next step
Continue to the next step
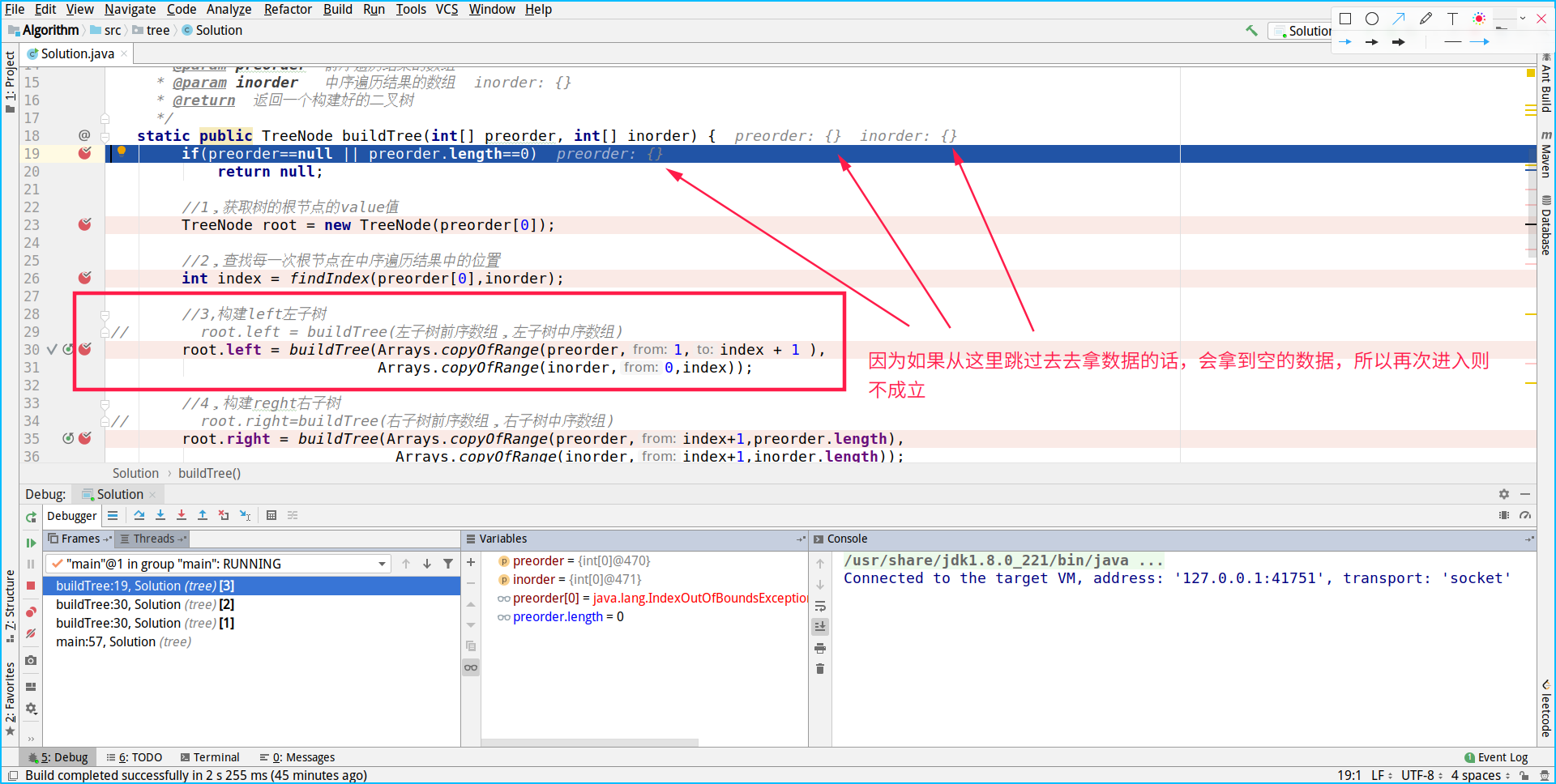
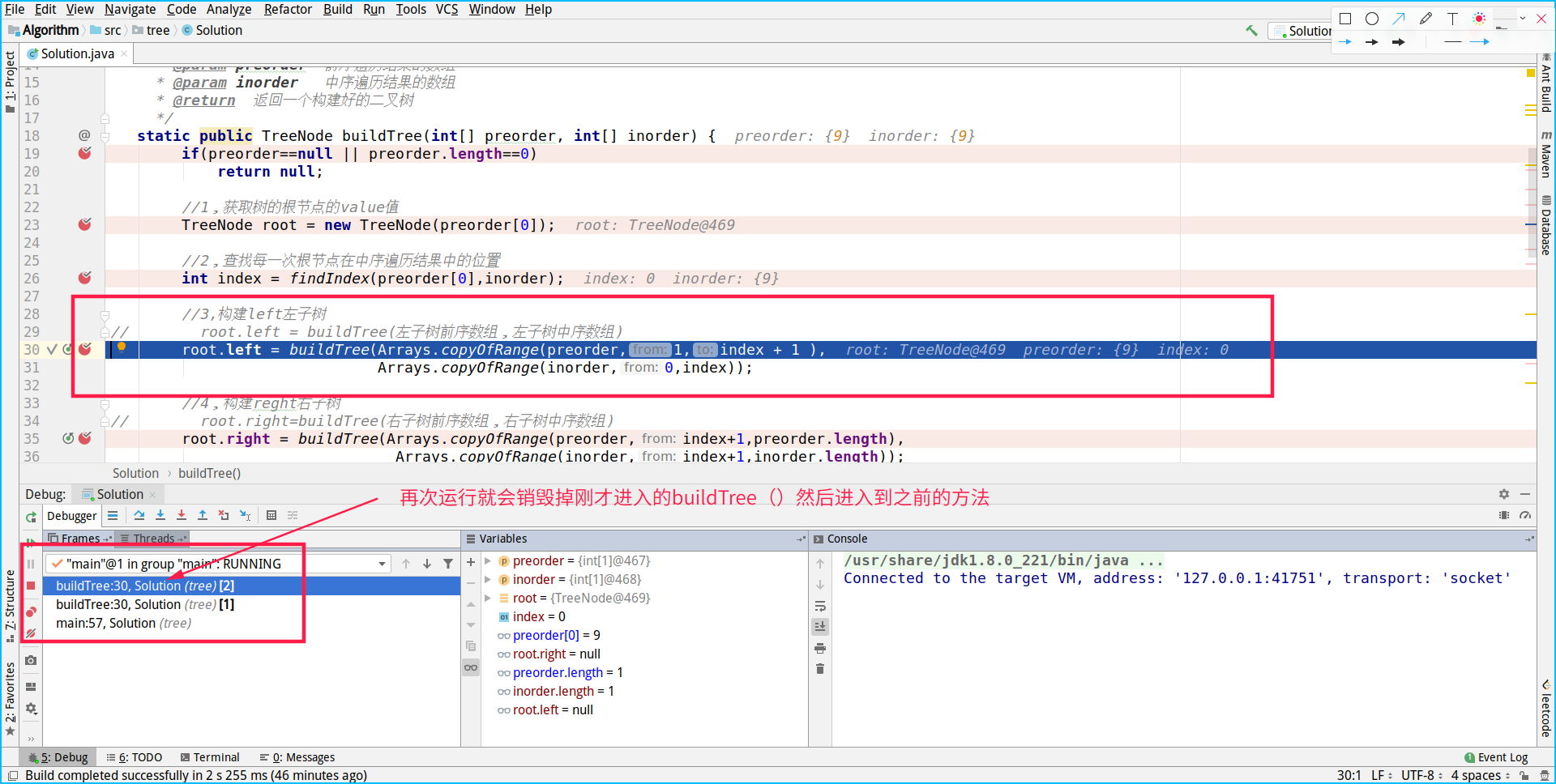
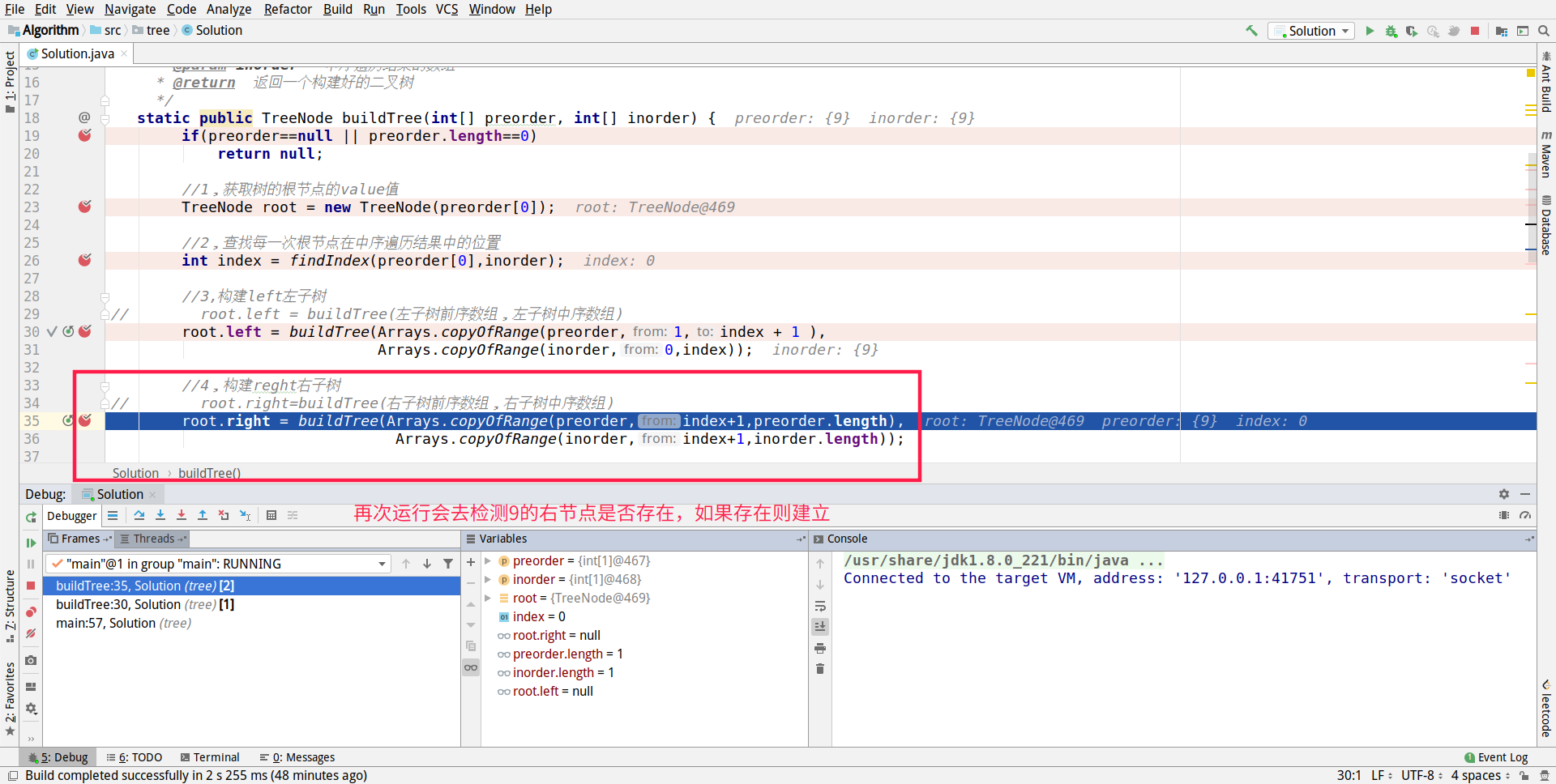
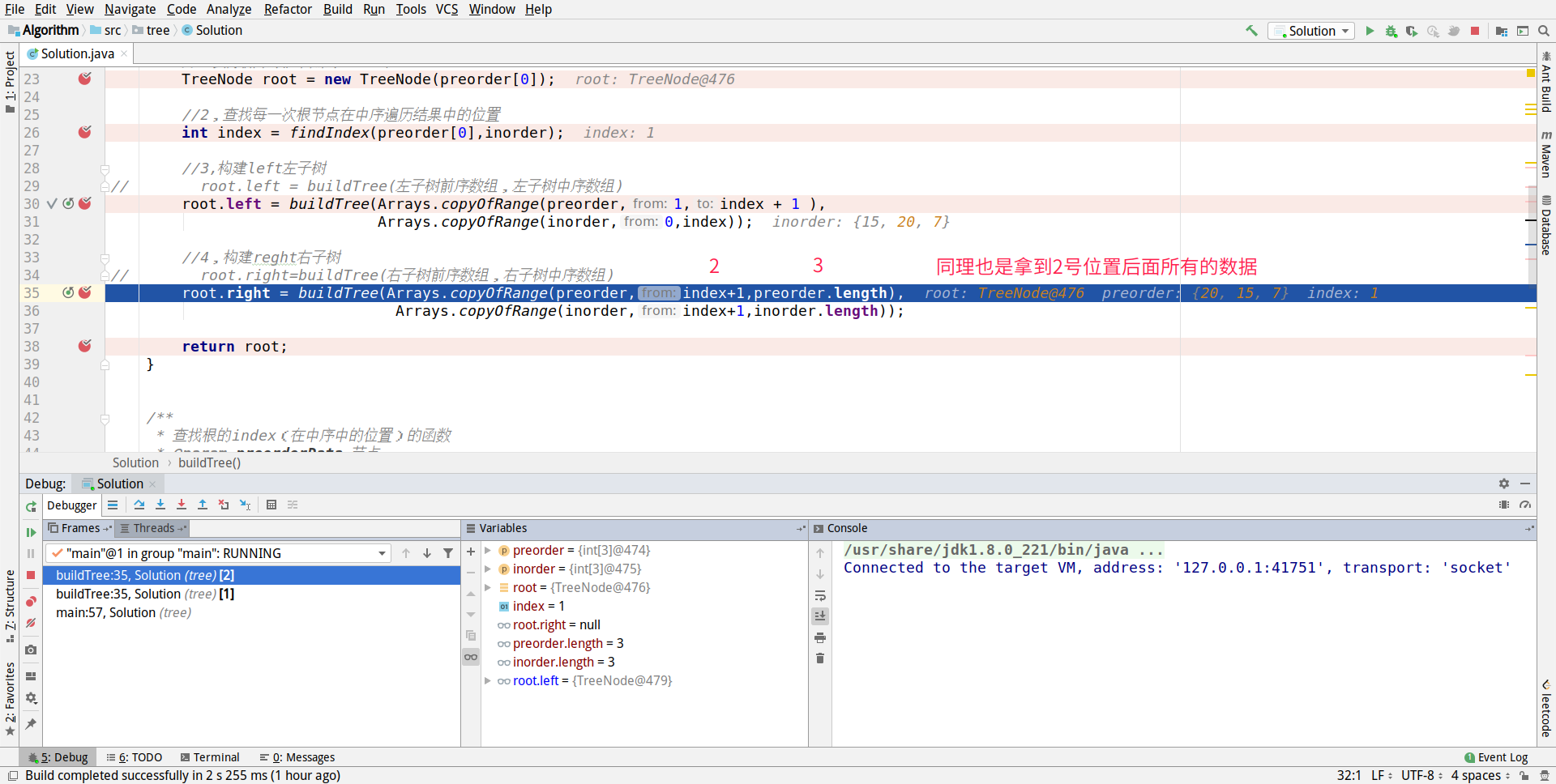
Start constructing all nodes on the right of 3:
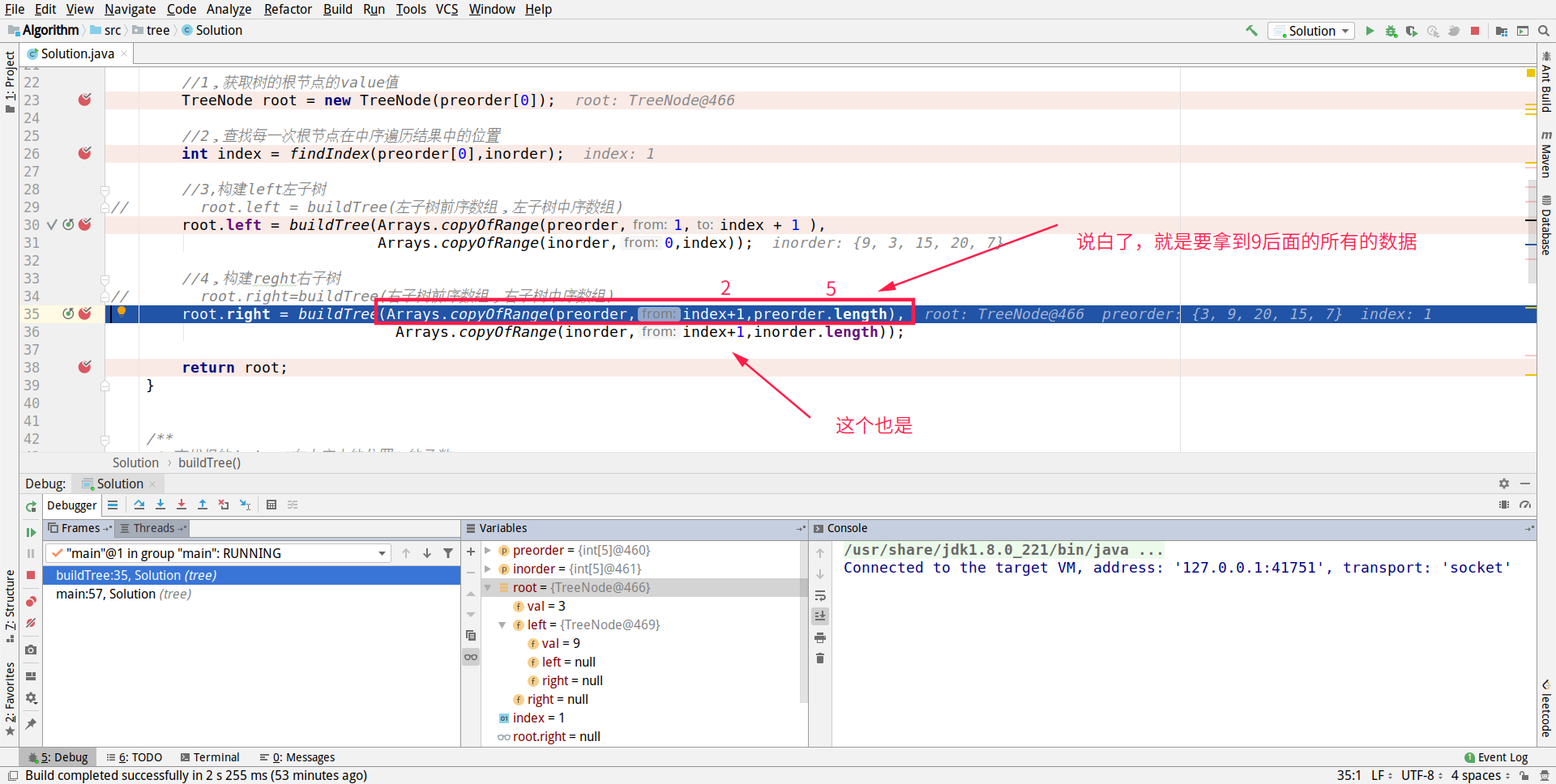
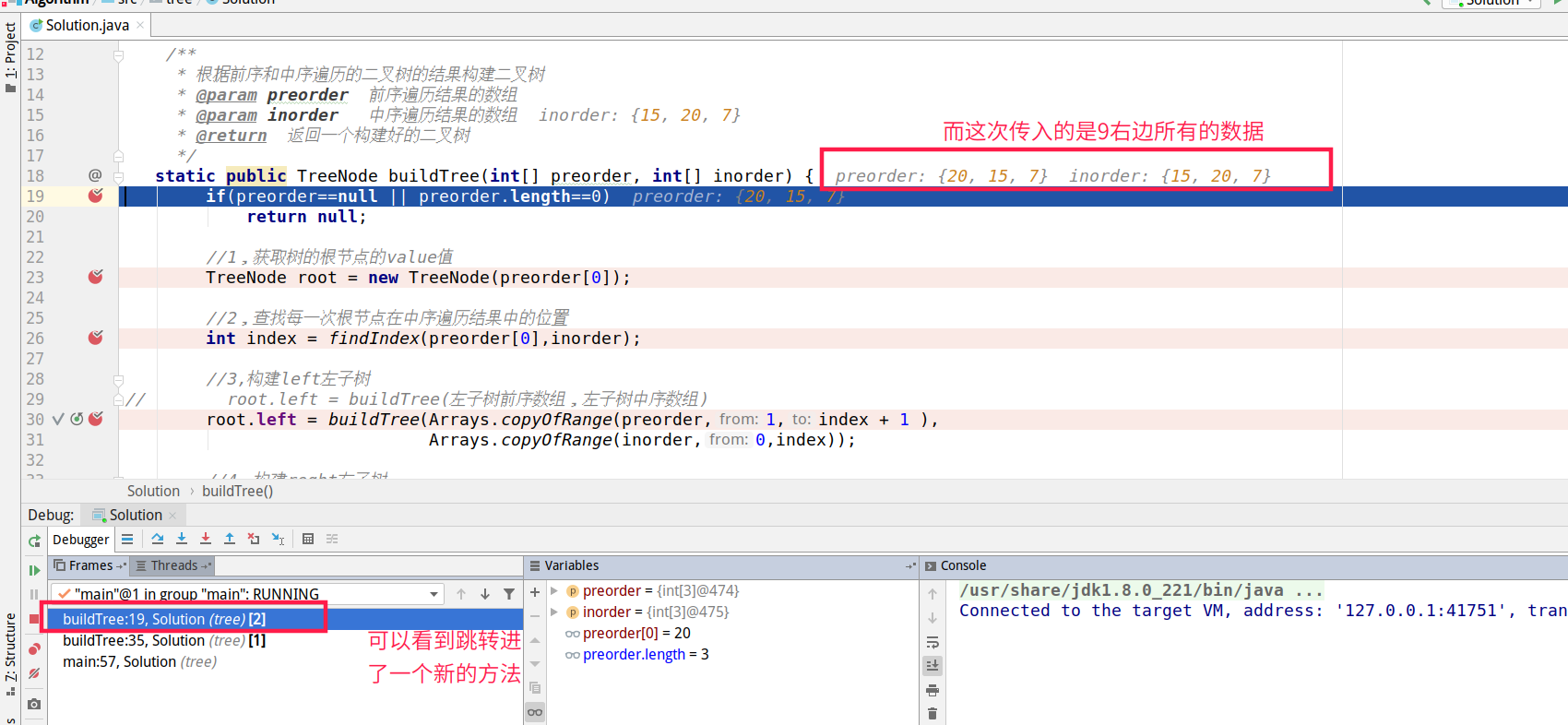

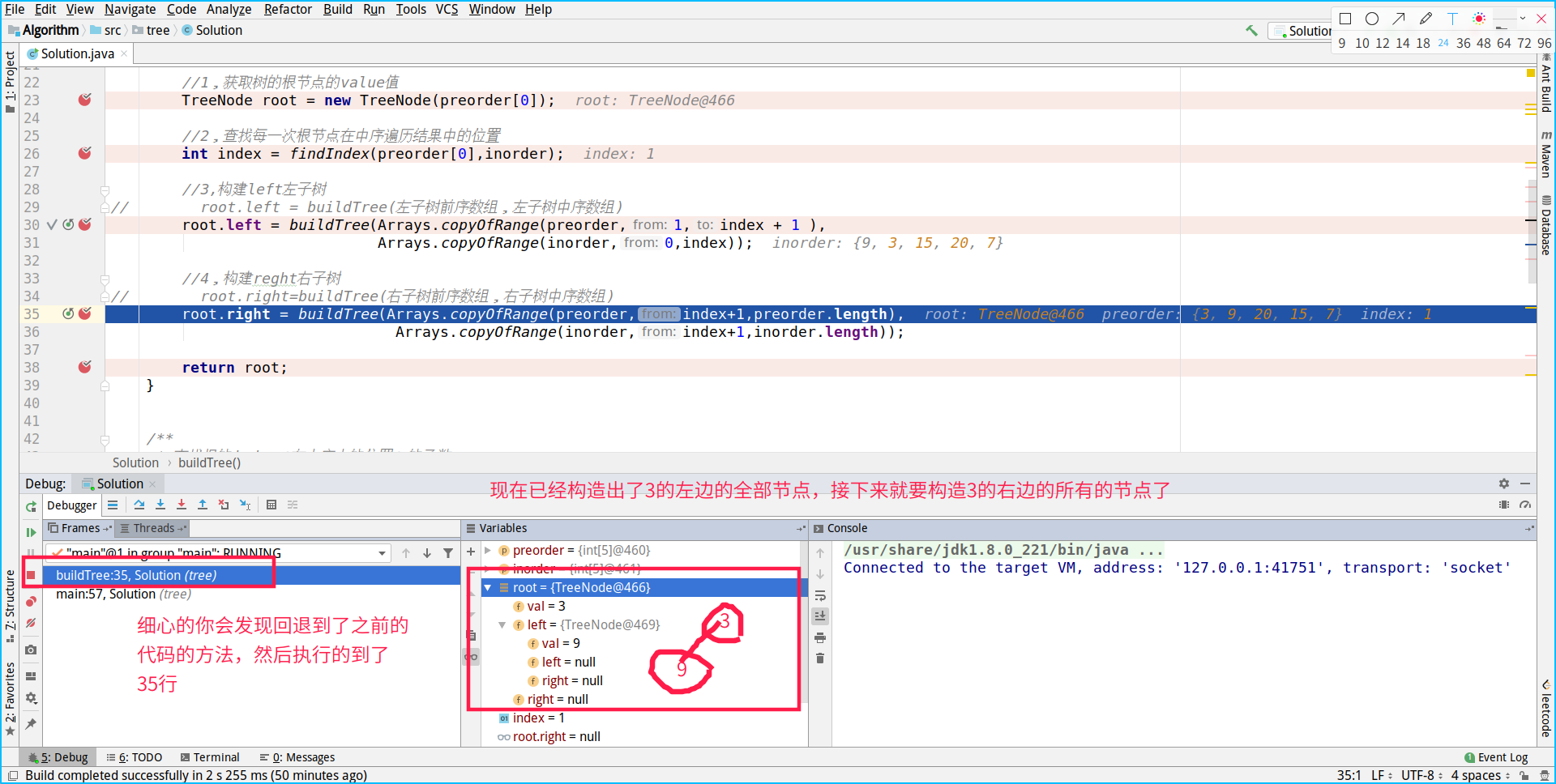
So we get the left node of 20
Now you can construct the last node, but because it is executed sequentially, n steps are omitted

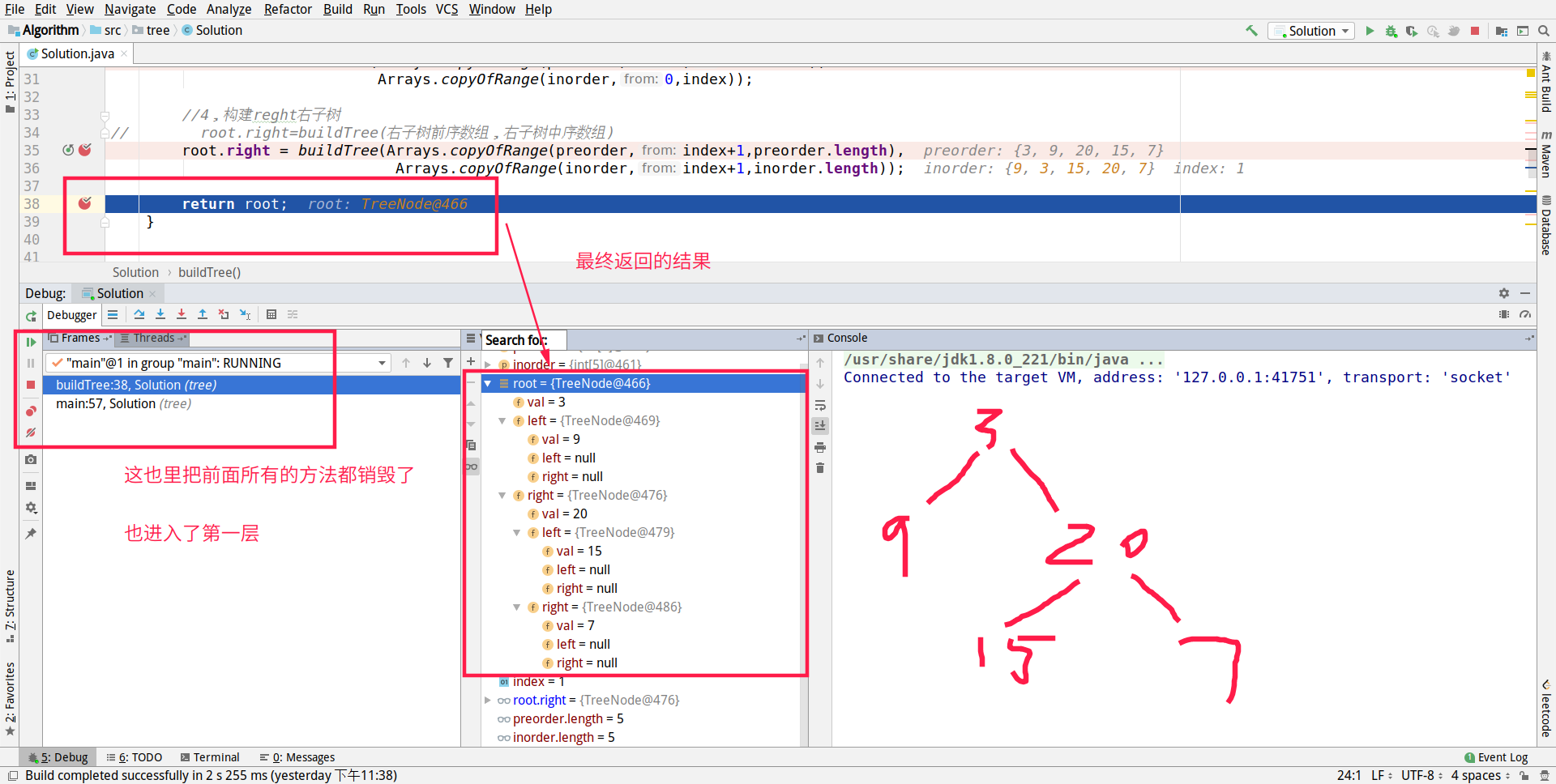
Verify that:
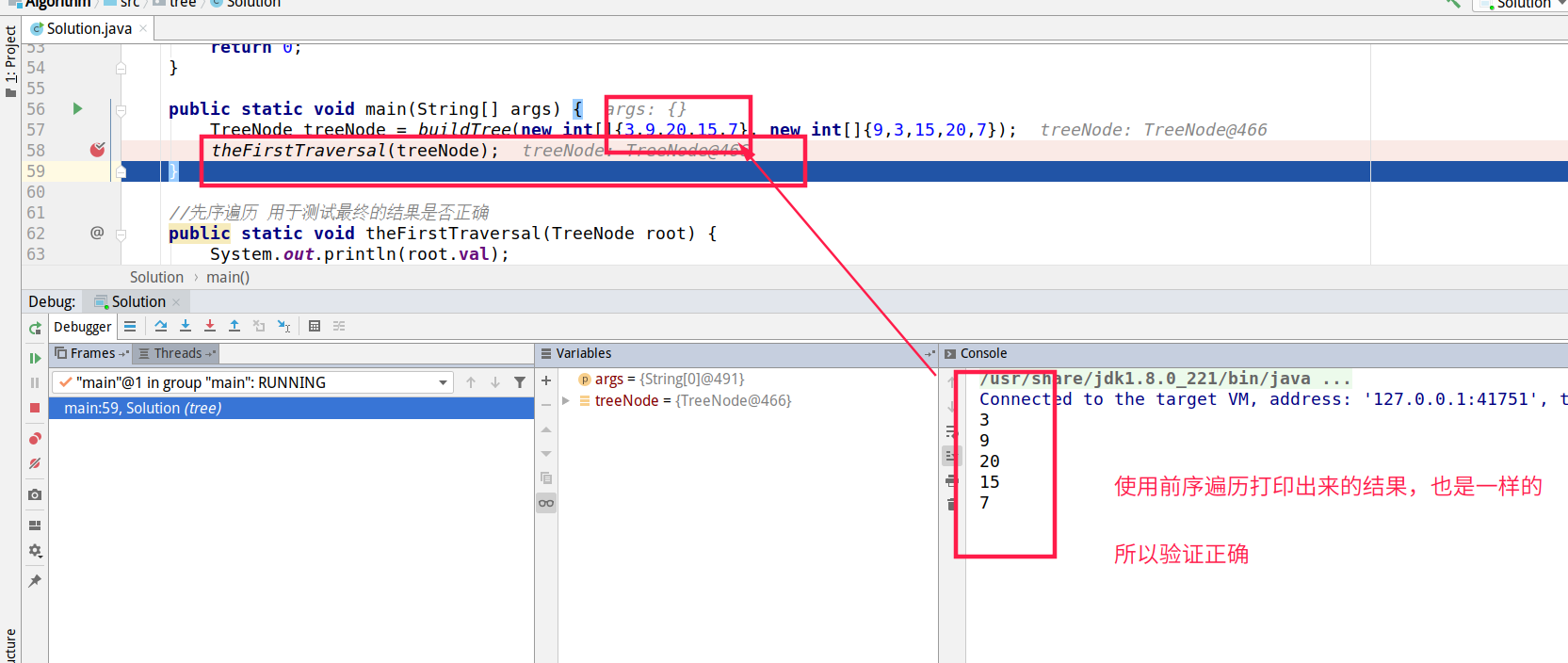
So far, that's it.
After Debug, my mind must be clear.
(5) AppendixArrays.copyOfRangeUsage of ()
Use System.arraycopy Similar to making array copies, Arrays provides a copyOfRange method for making array copies.
Arrays.copyOfRangeThe format of () is as follows:
- The first parameter represents the source array
- The second parameter represents the starting position (obtained)
- The third parameter indicates the end position (not available)
copyOfRange(int[] original, int from, int to)
Instance code:
import java.util.Arrays; public class HelloWorld { public static void main(String[] args) { int a[] = new int[] { 18, 62, 68, 82, 65, 9 }; // The difference is System.arraycopy, the target array needs to be prepared beforehand and the length allocated. // CopOfRange only needs the source array, and by returning a value, you can get the target array. // In addition, it is important to note that the third parameter of copyOfRange, which represents the end of the source array, is not accessible. // copyOfRange(int[] original, int from, int to) // The first parameter represents the source array // The second parameter represents the starting position (obtained) // The third parameter indicates the end position (not available) int[] b = Arrays.copyOfRange(a, 0, 3); for (int i = 0; i < b.length; i++) { System.out.print(b[i] + "\t");//18 62 68 } //Overflow Copy System.out.println(); int[] C = Arrays.copyOfRange(a, 0, 7); for (int i = 0; i <C.length; i++) { System.out.print(C[i] + "\t");//18 62 68 82 65 9 0 } } }
Reference address here:
Basic Java Learning - Copying Arrays Arrays.copyOfRange() Method Explanation
2. What Xiao Zheng You said
If it helps you, share it with your friends.Or give me a big compliment and comment, which is my greatest support, thank you.
Limited level, inevitably there will be omissions or unreasonable writing, welcome to exchange discussions.
Author: TrueDei
Author's only blog CSDN: https://truedei.blog.csdn.net/
Reproduction instructions: If you need to reproduce, please indicate the original address and author name.
If I like my articles and haven't seen enough to follow me, I'll write each one with my heart.
Welcome the big guys to join the small clubs below, where you can open up the communication and learn and progress together:
Officer, nod approval before you go