I Introduction to red and black trees
- Red black tree (R-B tree for short) is a special binary search tree.
- Red black tree is a special binary search tree, which means that it meets the characteristics of binary search tree: the key value contained in any node is greater than or equal to the key value of the left child and less than or equal to the key value of the right child.
Characteristics of red black tree:
- Each node is either black or red.
- The root node is black.
- Each leaf node is black. [leaf node is a node that is only empty (NIL or null).]
- If a node is red, its child nodes must be black.
- All paths from a node to its descendants contain the same number of black nodes, and ensure that no path is twice as long as other paths.
II Red black tree
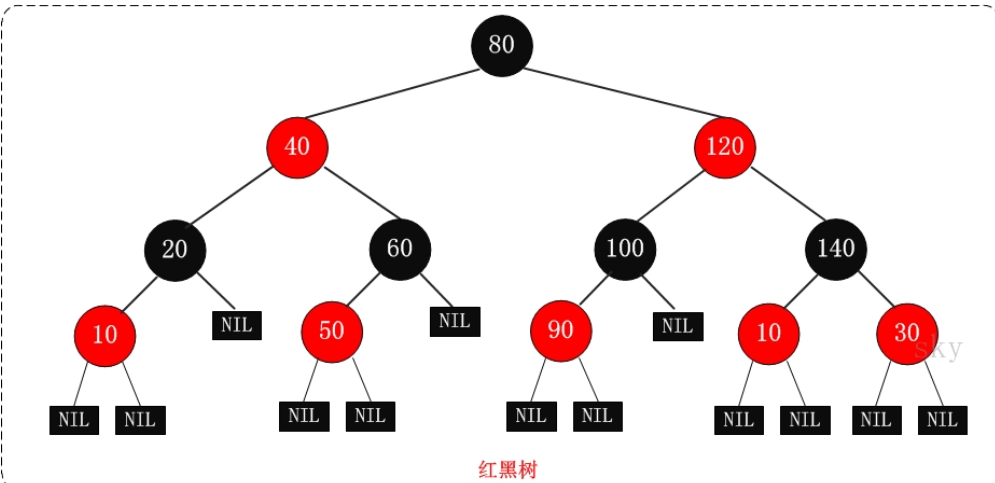
III Source code analysis red black tree
- The basic operations of red black tree are adding, deleting and rotating
I will directly use the red and black trees in HashMap for analysis
①. Basic definition of red black tree
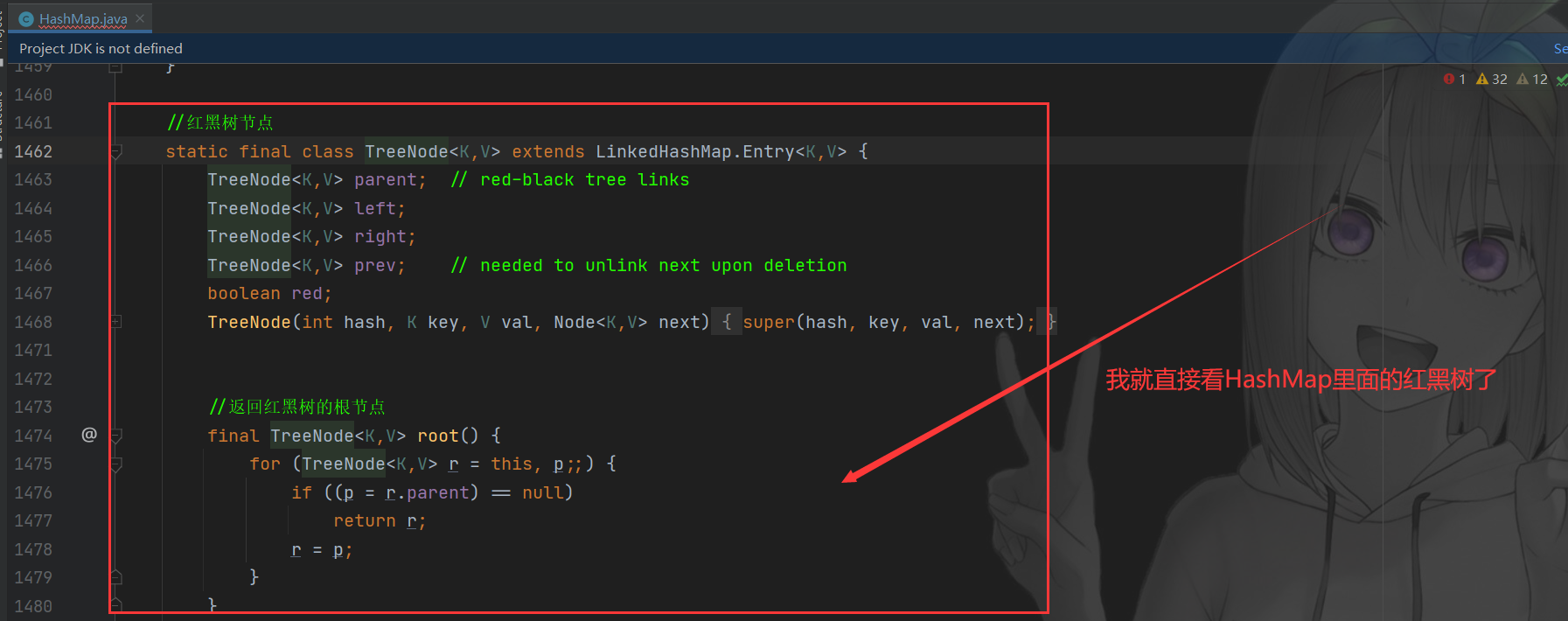
//Red black tree node
static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
TreeNode<K,V> parent; // red-black tree links
TreeNode<K,V> left;
TreeNode<K,V> right;
TreeNode<K,V> prev; // needed to unlink next upon deletion
boolean red;
TreeNode(int hash, K key, V val, Node<K,V> next) {
super(hash, key, val, next);
}
//Returns the root node of the red black tree
final TreeNode<K,V> root() {
for (TreeNode<K,V> r = this, p;;) {
if ((p = r.parent) == null)
return r;
r = p;
}
}
②. Sinistral
The above figure is copied online
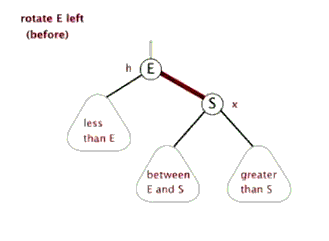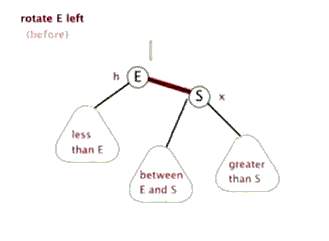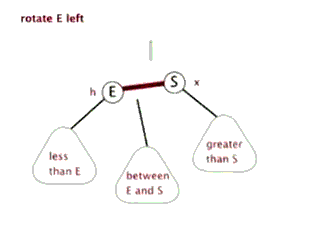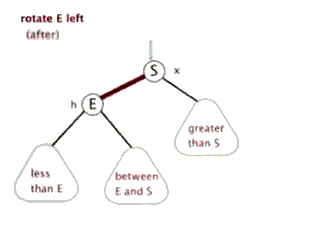
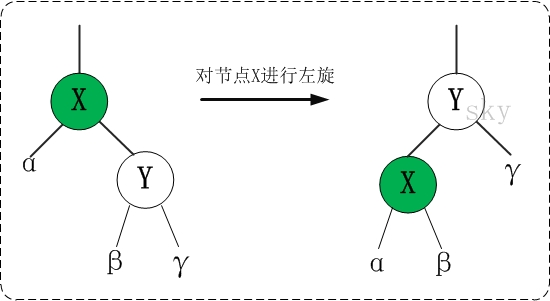
/*
* Rotate the node (x) of the red black tree to the left
*
* Schematic diagram of left rotation (left rotation of node x):
* px px
* / /
* x y
* / \ --(Left handed) -. / \#
* lx y x ry
* / \ / \
* ly ry lx ly
*
*
*/
private void leftRotate(RBTNode<T> x) {
// Set the right child of x to y
RBTNode<T> y = x.right;
// Set "left child of y" to "right child of x";
// If y's left child is not empty, set "x" to "Y's left child's father"
x.right = y.left;
if (y.left != null)
y.left.parent = x;
// Set "father of x" to "father of y"
y.parent = x.parent;
if (x.parent == null) {
this.mRoot = y; // If the parent of x is an empty node, set y as the root node
} else {
if (x.parent.left == x)
x.parent.left = y; // If x is the left child of its parent, set y to "the left child of X's parent"
else
x.parent.right = y; // If x is the left child of its parent, set y to "the left child of X's parent"
}
// Set "x" to "y's left child"
y.left = x;
// Set "parent of x" to "y"
x.parent = y;
}
③. Dextral
The above figure is copied online
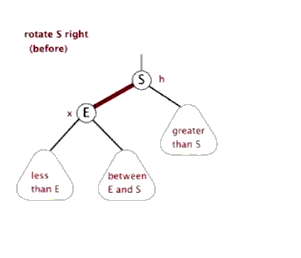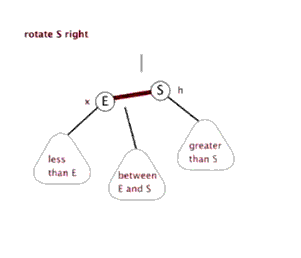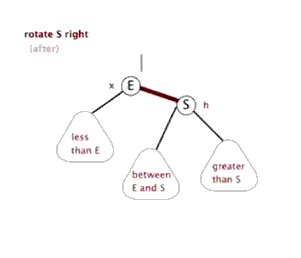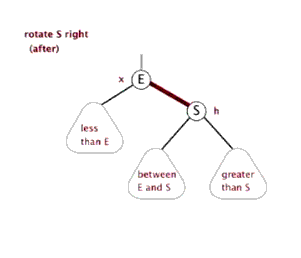
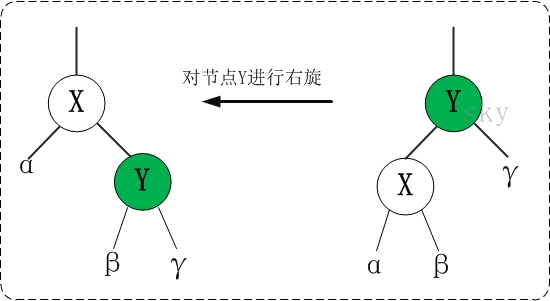
/*
* Rotate the node (y) of the red black tree to the right
*
* Schematic diagram of right rotation (left rotation of node y):
* py py
* / /
* y x
* / \ --(Right handed) -. / \#
* x ry lx y
* / \ / \ #
* lx rx rx ry
*
*/
private void rightRotate(RBTNode<T> y) {
// Set x to be the left child of the current node.
RBTNode<T> x = y.left;
// Set "right child of x" to "left child of y";
// If "x's right child" is not empty, set "y" to "x's right child's father"
y.left = x.right;
if (x.right != null)
x.right.parent = y;
// Set "father of y" to "father of x"
x.parent = y.parent;
if (y.parent == null) {
this.mRoot = x; // If "y's father" is an empty node, set x as the root node
} else {
if (y == y.parent.right)
y.parent.right = x; // If y is the right child of its parent node, set x as "the right child of Y's parent node"
else
y.parent.left = x; // (y is the left child of its parent node) set x as "the left child of x's parent node"
}
// Set "y" to "right child of x"
x.right = y;
// Set "parent node of y" to "x"
y.parent = x;
}
④. Add operation
Step 1: treat the red black tree as a binary lookup tree and insert the node.
- The red black tree itself is a binary lookup tree. After inserting nodes, the tree is still a binary lookup tree. That means that the key values of the tree are still in order. In addition, whether it is left-handed or right-handed, if the tree is a binary lookup tree before rotation, it must still be a binary lookup tree after rotation. This means that any rotation and recolor operation will not change the fact that it is still a binary lookup tree.
Step 2: shade the inserted node as "red".
- (5) All paths from a node to its descendants contain the same number of black nodes.
- Coloring the inserted node in red will not violate the "property (5)"! Fewer violations of a feature mean fewer situations we need to deal with.
Step 3: make it a red black tree again through a series of operations such as rotation or coloring. [four cases]
-
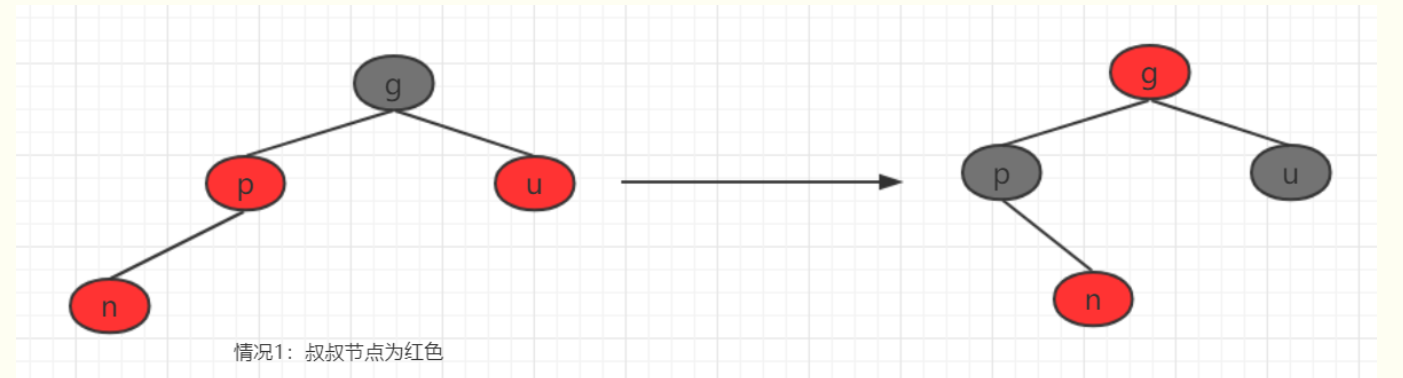
Case 1: the new node is the left node and the uncle node is red;
-
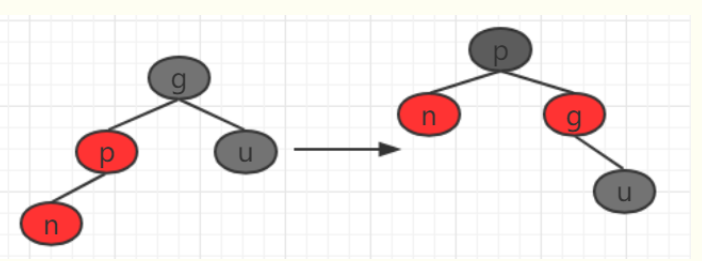
Case 2: the new node is the left node and the uncle node is black;
-
Case 3: the new node is the right node and the uncle node is red;
-
Case 4: the new node is the right node and the uncle node is black;
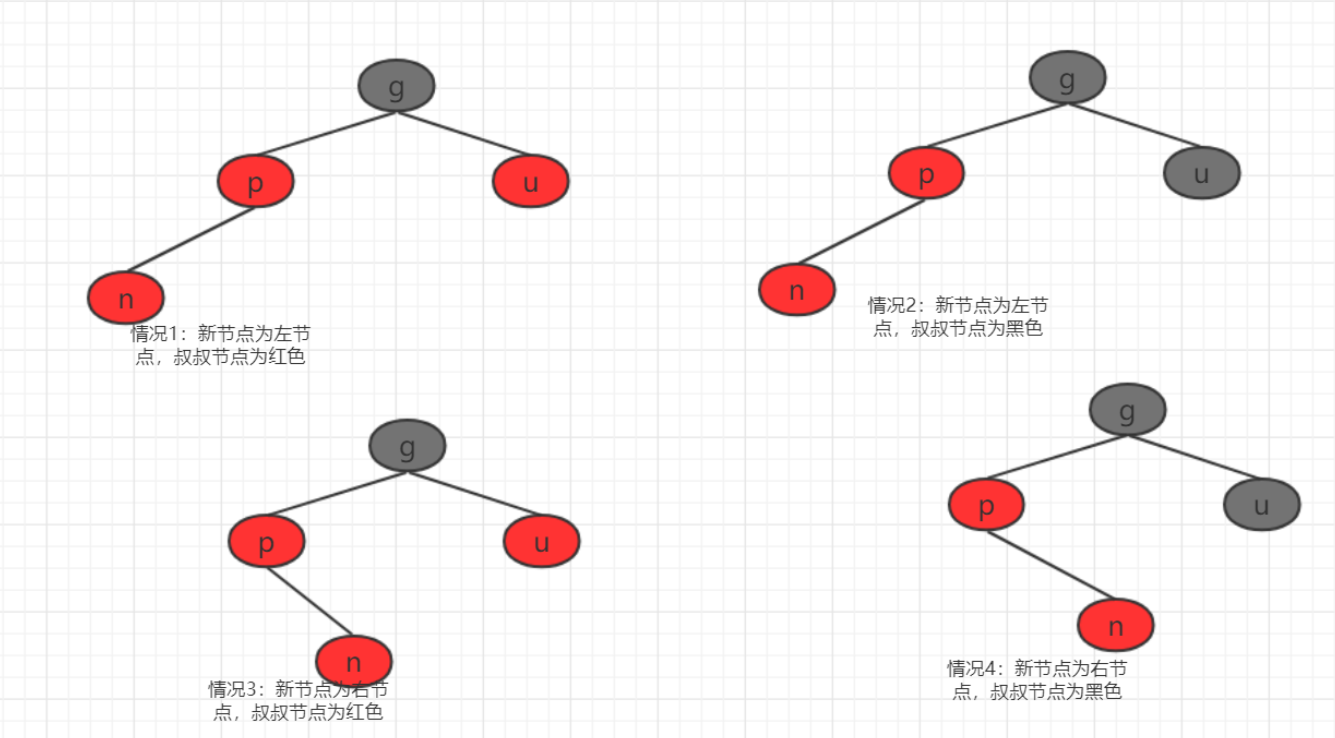
Scenario 1 and scenario 3 solutions
Scenario 2 and scenario 4 Solutions
⑤. Delete operation
Step 1: treat the red black tree as a binary lookup tree and delete the node. [in three cases]
- ①. The deleted node has no son, that is, it is a leaf node. Then, delete the node directly.
- ② . The deleted node has only one son. Then, delete the node directly and replace its position with the only child node of the node.
- ③. The deleted node has two sons. Then copy "the content of its successor node" to "the content of this node"; After that, delete its successor node. Here, the successor node is equivalent to a substitute. After copying the contents of the successor node to the "deleted node", the successor node is deleted. In this way, the problem is cleverly transformed into the case of "deleting successor nodes". Next, consider the successor nodes.
Step 2: modify the tree through a series of "rotation and recolor" to make it a red black tree again.
- Because deleting a node in step 1 may violate the characteristics of the red black tree. Therefore, the tree needs to be modified by "rotation and recolor" to make it a red black tree again.