HashMap bottom hyperdetailed interpretation

First, substitute a question: how does the underlying HashMap find the corresponding stored array node through the Key?

Look at the figure first to know what the underlying storage structure of HashMap is like

In the first case, the length of the linked list at the node position of the same array is less than 8, which is stored with an ordinary linked list

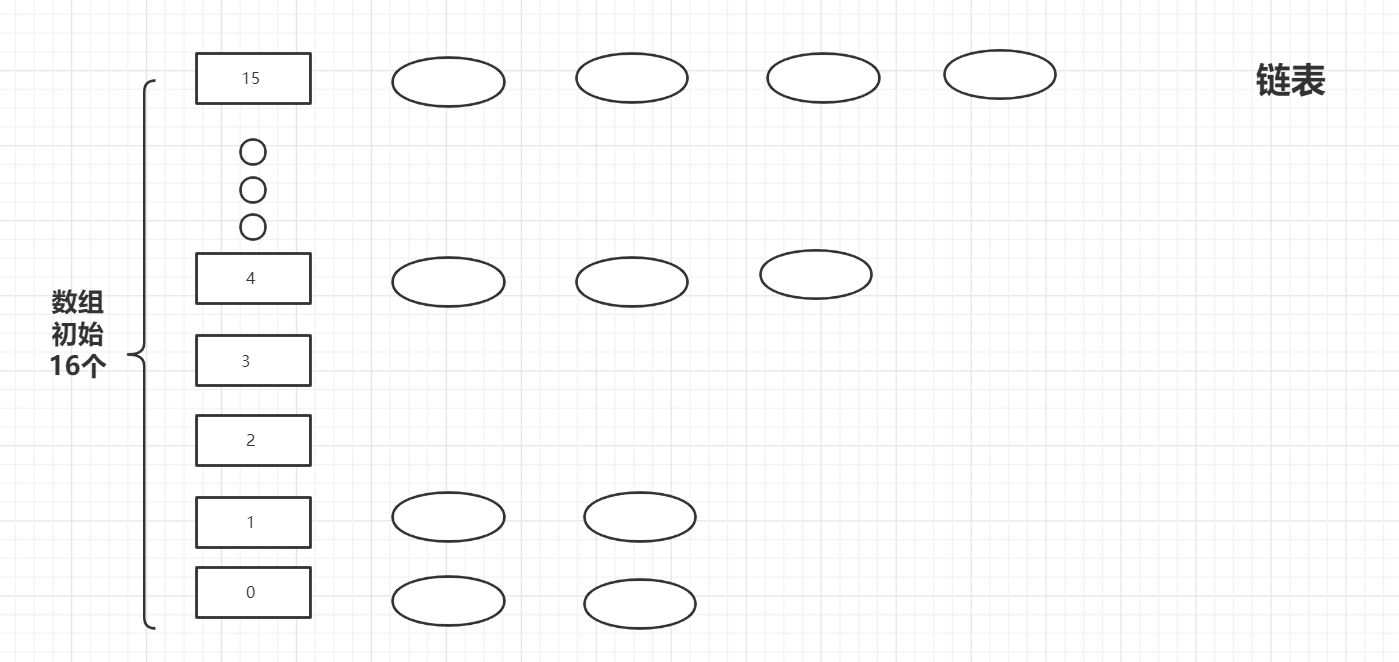
In the second case, when the length of the linked list at the node position of the same array is greater than 8, it is stored with a red black tree

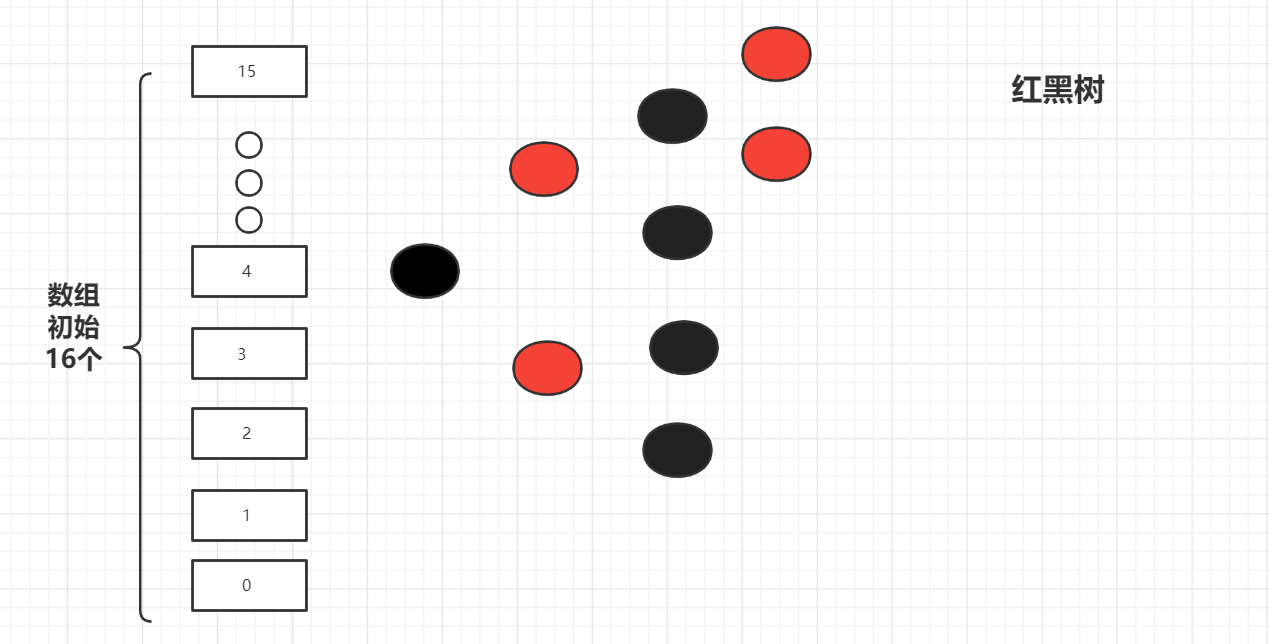
Next, analyze the source code

1. Create a HashMap object. HashMap uses the lazy style of singleton mode. It will be instantiated only when the method of the object is actually called

HashMap hash = new HashMap();
hash.put(1,"Zhang San");

2. After entering the put() method, we can see that the putVal() method is called again. This method is the specific method to store data

public V put(K key, V value) {
        return putVal(hash(key), key, value, false, true);
    }

The putVal() method has five parameters

2.1 the first hash(key) method is to get the index value of the storage array through the key and enter the hash() method

static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

We can see that when key==null, the returned result is 0, otherwise (H = key. Hashcode()) ^ (H > > > 16) operation is performed and the result is returned,

So here's a question: why can't we directly return the hashCode of the key and perform such a complex operation?

Because the return value type of hashCode() method is int type, 4 bytes, i.e. 32 bits, which can store 2 ^ 32 * 2 data, - (2 ^ 32-1) ~ (2 ^ 32-1), and the data we get is the subscript of the array to be stored, which is 16 by default (0 ~ 15). Obviously, 2 ^ 32 is much larger than 16, and the return result is very likely not to be in the range of 0 ~ 15, so we can't directly return the result of hashCode, Therefore, it is necessary to perform XOR operation between hashCode and its own high 16 bits. The purpose is to mix the high and low bits of the original hash code, so as to increase the randomness of the low bits and reduce the value as much as possible.

Then we can do some operations on it to make the range of the obtained results into the range of 0 ~ 15

• Step 1, H = key hashCode(), get the value of hashCode
• The second step is to shift h to the right by 16 bits without sign
• The third step is to sum with the original hashCode

Let's take an example

First step:hypothesis hashCode The value of is 1111 1111 1111 1111 0101 1101 0000 1101,that is h Value of variable
 Step two:hold h Unsigned right shift 16 bits, preceded by 0
    After moving right:0000 0000 0000 0000 1111 1111 1111 1111
 Step 3:Put the original h XOR with the result shifted to the right(Same as 0,The difference is 1)
	customary:1111 1111 1111 1111 0101 1101 0000 1101
    After moving right:0000 0000 0000 0000 1111 1111 1111 1111
    After XOR:1111 1111 1111 1111 1010 0010 1111 0010

The final data after XOR is passed into the putVal() method as a hash value. There is such a line in the putVal() method

//tab is the array. N is the length of the array. N-1 is because the subscript starts from 0. Use n-1 to sum with the hash result just obtained. Here, assume that n is the default 16 and N-1 = = 15
//hash:1111 1111 1111 1111 1010 0010 1111 0010
//15  :0000 0000 0000 0000 0000 0000 0000 1111
//i   :0000 0000 0000 0000 0000 0000 0000 0010
//And operation, both of which are 1, is 1. Because of the sum operation with 15, the result cannot be greater than 15, and the range is between 0 and 15. From the result of and operation, i==2
//That is, the subscript stored in the array is 2
//Here is to judge whether there are elements in the subscript position of the array. If it is null, it means that there is no node node in this position. Then it is ok to directly create a node and put it in
if ((p = tab[i = (n - 1) & hash]) == null)
        tab[i] = newNode(hash, key, value, null);

3. Enter putVal() method again

Here, we first need to understand the construction of node linked list nodes. The following methods are useful to the node class. Let's go to the node class and have a look

static class Node<K,V> implements Map.Entry<K,V> {
    final int hash;
    final K key;
    V value;
    Node<K,V> next;
        return false;
    }
}

You can find that the Node class inherits the Map Entry interface, while Map The entry interface can be regarded as a Map collection that only holds a set of data

It is also a key value pair that saves data, but there is only one set of data. There is also a getkey() getvalue() method

So a node node is actually saved in this way

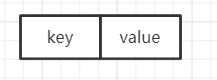
Let's look back at the putVal() method

final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
               boolean evict) {
    //Create a Node array tab, which is the hash bucket
    Node<K,V>[] tab; Node<K,V> p; int n, i;
    //Judge whether the array is empty. If it is empty, create an array
    //The array of HashMap is created late, which is also an optimization mechanism
    if ((tab = table) == null || (n = tab.length) == 0)
        //resize is the method of creating arrays and expanding arrays. Here, an array with a length of 16 is created, and its length is recorded with N, n=16
        n = (tab = resize()).length;
    //Take out the array element through the index and judge whether it is null
    if ((p = tab[i = (n - 1) & hash]) == null)
        //If it is null, directly create a Node to store
        tab[i] = newNode(hash, key, value, null);
    else {
        //If it is not null, judge whether the key s are the same
        Node<K,V> e; K k;
        if (p.hash == hash &&
            ((k = p.key) == key || (key != null && key.equals(k))))
            //If the same, directly overwrite the original value
            e = p;
        //If not, you need to add a new Node based on the original Node
        //First, judge whether the location is a linked list or a red black tree
        else if (p instanceof TreeNode)
            //If it is a red black tree, store the Node in the red black tree
            e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
        else {
            //If it is a linked list, traverse the linked list
            for (int binCount = 0; ; ++binCount) {
                //Find the last one
                if ((e = p.next) == null) {
                    //Add Node to the last bit of the linked list
                    p.next = newNode(hash, key, value, null);
                    //If the length exceeds 8, you need to turn the linked list into a red black tree
                    if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                        treeifyBin(tab, hash);
                    	//Enter treeifyBin method
                        <!-- start -->
                            //When the length of the array is less than 64, it will not be converted into a red black tree, but the capacity of the array will be expanded
                            //If you can use arrays, try to use arrays, because array query is the most efficient
                            //MIN_ TREEIFY_ Capability is 64
                            if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
                                resize();
                            else if ((e = tab[index = (n - 1) & hash]) != null) {
                        <!-- end -->
                    break;
                }
                //If there are duplicate key values in the linked list, directly assign the current element to p for replacement
                if (e.hash == hash &&
                    ((k = e.key) == key || (key != null && key.equals(k))))
                    break;
                p = e;
            }
        }
        if (e != null) { // existing mapping for key
            V oldValue = e.value;
            if (!onlyIfAbsent || oldValue == null)
                e.value = value;
            afterNodeAccess(e);
            //Returns the overwritten value
            return oldValue;
        }
    }
    //modCount is the number of modifications
    ++modCount;
    //Number of nodes++ 
    //threshold=capacity* loadFactor=16*0.75=12
    if (++size > threshold)
        resize();
    afterNodeInsertion(evict);
    //If the key is not repeated, null is returned
    return null;
}

Describe the logic in words again

1,according to key calculation hash Value.
2,stay put To determine whether the array exists. If it does not exist, use resize Method to create an array with a length of 16.
3,Are you sure you want to deposit node Position in the array, according to hash The subscript is obtained by bitwise sum with the maximum index of the array.
4,Judge whether there is an element in this position. If not, create one directly Node Deposit.
5,If there are elements, judge key Whether it is the same. If it is the same, overwrite and return.
6,If different, it needs to be in the original Node Add new Node，First, judge whether the location is a linked list or a red black tree.
7,If it is a red black tree, it will Node Deposited in red and black trees.
8,If it is a linked list, traverse the linked list and find the last bit Node Deposit.
9,take Node After saving, you need to judge whether the length of the linked list exceeds 8. If it exceeds 8, you need to convert the linked list into a red black tree. There is another condition. If the length of the array is less than 64, the array will be expanded again, and the conversion will be carried out only when the length of the array is greater than 64.
10,If the keys are the same and the values are different, the old value is taken out and returned, so put()Method actually has a return value
11,After adding, judge whether the array needs to be expanded.

Little knowledge

1.HashMap is created in a lazy way in the singleton mode. new HashMap will not create an array, but only define the loading factor. An array with a default length of 16 will be created only when the put method is called for storage

2. The loading factor of the array is 0.75. When the data stored in the array is greater than or equal to 16 * 0.75 = 12, the capacity will be resized (), and the capacity will be doubled

3. The size of the linked list cannot exceed or equal to 8, otherwise it will be converted to red black tree storage

4. Add a new node. When the length of the linked list is equal to 8, it will not turn into a red black tree immediately. You also need to judge whether the current array length is greater than 64. If it is less than 64, expand the array, and then calculate the array index subscript of the current object through key and hashCode, and then store it. The reason is that if you can use the array, you don't use the linked list and red black tree. After all, the query efficiency of the array is the highest

5. The put method also has a return value. When the key is not repeated, the return value is null. When the value of the same key is different, the old value is returned

6. There are two steps to find the array index,

• key. hashCode() ^ (key. hashCode() > > > 16) the hashCode of the key and the hashCode of the key are unsigned and shifted to the right by 16 for exclusive or
• Array length (n-1) & hash (the result obtained in the previous step)

The purpose is to mix the high and low bits of the original hash code, so as to increase the randomness of the low bits and reduce the value as much as possible.

Then perform & operation with n-1 to ensure that the final value range is [0,n-1]