Preface
When it comes to the implementation principle of HashMap, most of the little buddies think about the structure of "based on arrays and lists or red and black numbers" in their minds, and many people also say that during interviews. This answer is definitely impossible for the interviewer, and I find that the implementation principle of hashMap is also a must-ask point for interviews. Probably 9 out of 10 times will ask (don't believe it's OK to ask Boil C or Goat, ==), so HashMap is still a very important point, so I'll learn HashMap with your little buddies, let's go...
text
Before we get to know HashMap, let's start with a few important concepts. These are the preconditions for realizing HashMap. Here's just a brief introduction. As for the detailed implementation, you can go to Bing Bing (you don't like Baidu personally), or you can have the opportunity to publish several articles about this. You will remember to look at....
1. Hash algorithm (hash algorithm)
The Hash algorithm maps any length of binary plaintext to a shorter binary string, and it is difficult for different plaintext to map to the same Hash value (but there are also hash conflicts, that is, different plaintext maps to the same Hash value).
It can also be understood as a spatial mapping function, which maps from a very large value space to a very small value space. Because it is not a one-to-one mapping, the Hash function is not invertible after conversion, which means it is impossible to restore the original value through inversion and Hash values.
Hash algorithm is also called hash algorithm. Although Hash algorithm is called algorithm, it is actually more like a thought.
2. Hash Table
A Hash table is a data structure that is directly accessed based on a key value. That is, it accesses records by mapping key code values to a location in the table to speed up the search. This mapping function is called a hash function, and the array of records is called a hash list.
3. Chain List
A chain table is a discontinuous, non-sequential storage structure in a physical storage unit. The logical order of data elements is achieved by the order of pointer links in the chain table. A chain table consists of a series of nodes (each element in the chain table is called a node), which can be generated dynamically at run time. Each node consists of two parts: a data field storing data elements and a pointer field storing the address of the next node.
4. Black and Red Trees
Red-black tree is a specialized AVL tree (balanced binary tree), which maintains the balance of binary lookup trees through specific operations during insert and delete operations, thus achieving higher lookup performance.
It is complex, but its worst-case runtime is also very good and efficient in practice: it can find, insert, and delete in O(log n), where n is the number of elements in the tree.
(The above content is abstracted from the network, the specific implementation principle is not described here....)
HashMap principles
First, let's take a look at the HashMap schematic, which is half the way through
HashMap schematic
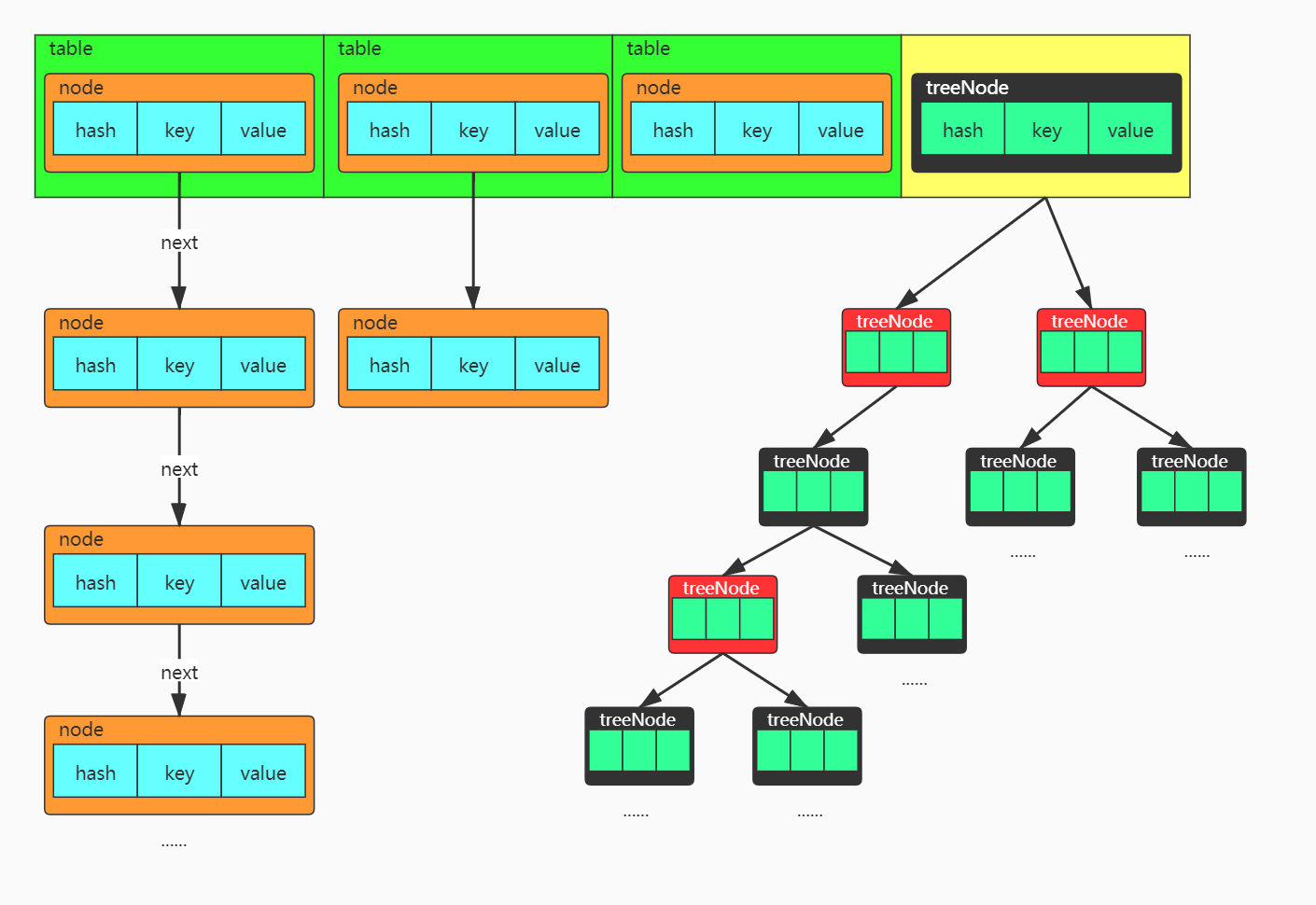
HashMap structure:
jdk1.7:Entry Array+Chain List
jdk1.8:Node Array + Chain List or Red-Black Tree (Chain List is converted to Red-Black when Chain List Length is greater than or equal to 8)
HashMap stores key-value pairs in Node arrays, and each key-value pair makes up Node entities. The Node class is actually a one-way chain table structure with a Next pointer that connects the next Node entities. In JDK1. In 8, when the degree of chain table is equal to 8, the chain table will turn into a red tree!
This is when a little partner asks:
q1: Why is hashMa p structured as an array + Chain table?
To answer this question, we first have to know what is a hash conflict?
The hash algorithm above tells us that different plaintext may produce the same Hash value after hashing, and we assume that it has a hash conflict.
The hash values produced after the conflict are the same, and they get the same array subscript index, so to insert multiple values under the same array subscript, you need to use the chain table, jdk1.8 By using tail interpolation, that is, by inserting values with the same hash value (i.e., the same subscript index) at the end of the chain table, the structure can see the chain table shown in the first column of the HashMap schematic diagram above. Each chain table node has a next pointer to the next node.
q2: Why jdk1. What about the 8-link list becoming a mahogany?
Red-black tree is a special balanced binary tree. Its query time complexity is O (logn), and the query time complexity of chain table is O (n). In fact, the query efficiency of chain table is much higher than that of red-black tree, but in more and more cases, the query efficiency of red-black tree is higher than that of chain table. Initially, the list is not very long, so there may be little difference between O(n) and O(log(n)), but this difference will be reflected if the list is longer and longer. Therefore, in order to improve the search performance, the chain table needs to be converted into a red-black tree. In fact, in order to improve query efficiency, the chain table is converted to a red-black tree when its length is greater than or equal to threshold 8.
q3: Why not use red-black trees directly?
In fact, a single TreeNode occupies twice as much space as a normal Node. If the hash value is well distributed, that is, the hash calculation is well dispersed, the red and black trees are rarely used. Each value will be distributed more evenly, and very long chain tables rarely occur. When the chain table length equals 8, the probability is only 0.00000006, which is very small. Usually, you don't need to store that much data in a Map, so you rarely use red-black tree transformations. Therefore, considering the balance between time and space complexity, a chain table is converted to a red-black tree when its length is greater than or equal to 8 and a red-black tree when its length is less than or equal to 6. (This is explained below line 144 of the HashMap source.)
HashMap Source Parsing
Initialize a HashMap
First of all, when we use HashMap, we go to a new HashMap object, but HashMap actually has many constructs:
// Specify the construction of initial capacity and load factor
public HashMap(int initialCapacity, float loadFactor) {
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal initial capacity: " +
initialCapacity);
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException("Illegal load factor: " +
loadFactor);
this.loadFactor = loadFactor;
this.threshold = tableSizeFor(initialCapacity);
}
// Specify initial capacity and construction of default load factor
public HashMap(int initialCapacity) {
this(initialCapacity, DEFAULT_LOAD_FACTOR);
}
// Construction of default initial capacity and default load factor
public HashMap() {
this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
}
In fact, the last one we use most often is the parametric construction. The parameterless construction uses the default initial capacity and the default load factor.
q4: What is the initial capacity and load factor?
/**
* Default initial capacity must be a power of 2
*/
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16
/**
* Default Load Factor
*/
static final float DEFAULT_LOAD_FACTOR = 0.75f;
Without specifying the initial capacity and load factor, the constructor defaults to the value in the code above, which is the length of the initial array of 16, while the load factor indicates expansion when the storage data capacity reaches 75% of the initial capacity. The comment in the code shows that the initial capacity must be a power of 2, so the problem arises:
q5: Why must the initial capacity be a power of 2?
First, the purpose is to make the computed array subscript values fully hashed and minimize the chance of collision, thereby reducing space waste and increasing query speed.
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
······
Here is part of the source code for HashMap when put ting values, where if ((p = tab[i = (n - 1) & hash]) == null) I = (n - 1) & hash is used to calculate array subscripts, where n is the length of the array, & is the AND operation (operation rule: 0&0=0; 0&1=0; 1&1=1; that is, if both are "1", the result is "1", otherwise 0), So the above code is expressed as follows: the length of the array and the hash value are run and calculated to get the subscript, and then an ex amp le is given to illustrate why the length must be a power of 2: (assume the length of the array is 16, then n-1 = 15)
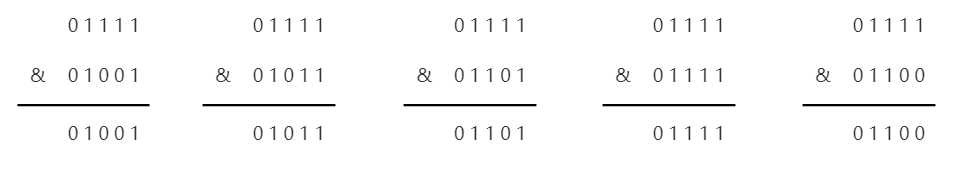
You can see that different values and 15 operations can get different subscripts.
If the length of the array is assumed to be 10, run and run with the same number and 9 as above
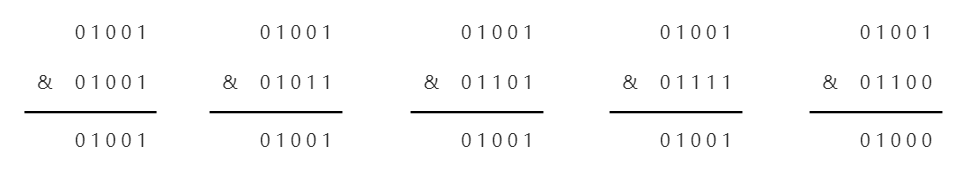
You can see that there are five numbers here, four of which all produce the same result, so they correspond to the same subscript in the array, that is, to insert the same position, which results in a very severe hash collision.
In fact, in order to fully hash array subscript values, there is also a key operation to calculate hash values before calculating subscript values. Let's first look at how to calculate hash values.
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
In the code above, H = key. HashCode() calculates a hashCode value h, and only one operation (h = key.hashCode()) ^ (h >>> 16) has been performed. What is this operation for?
Before we get to know this, let's first understand what ^ and >> mean:
^ // XOR: 1^1=0^0=0 1^0=1 0^1=1 =>The two are equal to 0, not equal to 1 (more complex operations look for themselves) >>> // Bit operation, unsigned right shift
That is, the calculated hash h h h is XOR with the unsigned right-shift value of H.
Because of the (n - 1) & hash operation, n (array length) is mostly less than 2 to the 16th power. So the lower 16 bits (or even lower) of the hash value always participate in the operation.
High 16 bits Low 16 bits hash 0101 0100 1011 0011 | 1101 1111 1110 0001 & n-1 0000 0000 0000 0000 | 0000 0000 0000 0111 = 0000 0000 0000 0000 | 0000 0000 0000 0001 (Is decimal 1, so the subscript is 1)
So 16 bits high is not useful. If 16 bits high is involved in the operation, the resulting subscripts will be more hashed. How do I get High 16 to participate in the calculation?
So the hashCode() you get is ^ computed with its own 16-bit height, so (h >>> 16) gets its 16-bit height, so you can see the calculation below.
High 16 bits Low 16 bits
hash 0101 0100 1011 0011 | 1101 1111 1110 0001
>>>16
0000 0000 0000 0000 | 0101 0100 1011 0011
^
0101 0100 1011 0011 | 1000 1011 0101 0010
If you do (n - 1) & hash on the resulting value, you will get a more hashed array subscript.
HashMap Expansion
Because hash conflicts cannot be completely avoided, in order to improve HashMap performance, hash conflicts have to be mitigated to shorten the length of each array's hang-in list (or red-black tree). When the array storage capacity reaches the threshold, an expansion of HashMap is required.
// Initial threshold is the default load factor*default initial capacity newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY); // threshold threshold = newThr;
HashMap's extension operation is in the resize() method. Because it's a long method, let's do a step-by-step explanation, OK. Let's get started.
final Node<K,V>[] resize() {
// Old table array
Node<K,V>[] oldTab = table;
// Old capacity
int oldCap = (oldTab == null) ? 0 : oldTab.length;
// Old threshold
int oldThr = threshold;
// New capacity and new threshold
int newCap, newThr = 0;
There are several key variables to note when entering the method first.
if (oldCap > 0) {
// Is old capacity greater than or equal to maximum capacity
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
// The new capacity is doubled, less than the maximum capacity, and the old capacity is greater than or equal to the default initial capacity
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
// Double the threshold
newThr = oldThr << 1; // double threshold
}
The code above mainly determines whether the old capacity has exceeded the maximum capacity that HashMap can store, and then does the corresponding operation on the threshold, as described in the comments.
else if (oldThr > 0)
// Initial capacity set to threshold
newCap = oldThr;
else {
// Zero initial threshold means default value is used
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
This section understands that if the old threshold is greater than 0 and the new capacity is set to the old threshold, no greater than 0, that is, the old HashMap has not been initialized (that is, HashMap was created using a parameterless construct where the true initialization is done), then the initial capacity of HashMap is set to the default initial capacity. The threshold is set to the initial threshold (described above).
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
If the new threshold is still 0 after the above operations, then an assignment operation is performed on the new threshold. The process is simple, let alone say.
Next is the steps for true expansion
@SuppressWarnings({"rawtypes","unchecked"})
// Initialize a new Node array with a new capacity
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
if (oldTab != null) {
// Traversing through old arrays
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
// If the array is not empty, it is assigned to e
if ((e = oldTab[j]) != null) {
// Old value set to null
oldTab[j] = null;
// The node next points to null, which is not a list of chains
if (e.next == null)
// Direct assignment, after calculating the subscript, assigns e to the position of the new array corresponding to the subscript
newTab[e.hash & (newCap - 1)] = e;
// If e is a red-black tree node
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else { // Divide the list into two parts
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
if ((e.hash & oldCap) == 0) {
// The node is placed in the same position as the old array in the new array
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
// The node places the new array at the index position of the array plus the length of the old array
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
In the above code (e.hash & oldCap) == 0 is computed to divide the old list into two new arrays of linked lists. For the reason why this is done, see the following explanation:
HashMap expands by creating a new array and then transferring data from the old array to the new one
In this case, the data on the old array is cleverly categorized into two categories based on whether (e.hash & oldCap) equals 0:
(1) When equal to 0, the index position of the header node in the new array is equal to its index position in the old array, which is marked as low at the beginning of the low-bit chain list lo;
(2) If it is not equal to 0, the index position of the header node in the new array is equal to its index position in the old array, and the length of the old array is added to mark it as high at the beginning of the high-bit chain table hi.
See the following algorithm derivation and analysis for details
Algorithms:
(e.hash & oldCap)=0
Prerequisite:
_e.hash represents the hash value of a node or element or data E in an old array, which is determined by the key: (key == null)? 0: (h = key.hashCode()) ^ (h >>> 16);
_oldCap is the length of the old array and is an integer of the nth power of 2. E.hash&2^n=0
Derivation process 1:
*** (e.hash & oldCap)=0: ***
Since oldCap is an integer of the N-power of 2, its binary expression is an 1 followed by n 0:1000...0. If you want the result of e.hash&oldCap to be 0, the position of 1 in the binary form of e.hash must be 0 for the corresponding oldCap, and the other positions can be arbitrary, so that the result can be guaranteed to be 0;
Assume:
oldCap= 2 ^ 3 =8 = 1000
Then e.hash can be 0101
e.hash&oldCap 0000=0
(2oldCap-1) =2 ^ 4-1=01111, which has one more binary digit than oldCap, but one more digit is 0, and the rest are 1 (the lower three must be 1).
(oldCap-1)=2 ^ 3-1=0111, its binary digits are the same as oldCap, and its lower 3 digits are all 1. Therefore, when (2oldCap-1) and (oldCap-1) are computed with e.hash=0101, which has only 4 bits and the first 0 bits, only the lower 3 bits can actually affect the result, while the lower 3 bits of both are the same, all 111;
So under the preceding conditions, (2oldCap-1) and (oldCap-1) both have the same results as after the e.hash&operation:
(2oldCap -1)=2 ^ 4-1= 01111
(oldCap-1)=2 ^ 3-1= 0111
e.hash 0101
e.hash&oldCap 00101=5
e.hash&oldCap 0101=5
(oldCap-1) &e.hash happens to represent the index position of the E element in the old array;
(2oldCap-1) &e.hash represents the index position of the E element in the new array after the length of the old array has been expanded two times
To sum up, the elements satisfying e.hash&oldCap=0 have the same index position in the old and new arrays.
Derivation process 2:
(e.hash & oldCap) is not equal to 0:
Because oldCap is an integer of the N-power of 2, its binary expression is an integer of 1 followed by n 0:1000...0. If you want the result of e.hash&oldCap to be non-zero, the position of 1 in the binary form of e.hash must not be zero, and the other positions can be arbitrary, so that the result is not zero.
Assume:
oldCap= 2 ^ 3 =8 = 1000
e.hash can be 1101
e.hash&oldCap 1000=13
(2oldCap-1) =2 ^ 4-1=01111, which has one more binary digit than oldCap, but one more digit is 0, and the rest are all 1 (the lower three digits are definitely 1, and the fourth digit from left to right is 1);
(oldCap-1)=2 ^ 3-1=0111, its binary digits are the same as oldCap, and its lower 3 digits are all 1, its fourth digit from right to left is 0,. So when (2oldCap-1) and (oldCap-1) are computed with e.hash=1101 with only 4 digits and the first 1 digit, only the fourth digit (0) from the right to the left actually affects the result, because the lower 3 digits are exactly the same as 1;
4. Therefore, under the preceding conditions, (2oldCap-1) and (oldCap-1) differ from e.hash in the results after the operation oldCap:
(2oldCap -1)=2^4-1= 01111
( oldCap - 1 ) =2 ^ 3-1= 0111
e.hash 1101
(2oldCap -1)& e.hash 01101=8+5
(2oldCap -1)&e.hash 0101=5
(oldCap-1) &e.hash happens to represent the index position of the E element in the old array;
(2oldCap-1) &e.hash represents the index position of the E element in the new array after the length of the old array has been expanded two times
To sum up, the elements that satisfy e.hash&oldCap is not equal to 0 can be found. Their index position in the new array is based on their index position in the old array plus an offset of the length of the old array.
The above derivation is referenced from Let the stars ⭐ The moon tells you that the rehash method (e.hash & oldCap) === 0 algorithm derivation for HashMap expansion I also think the push process is very good, so I can use it for reference here for everyone to learn
There is also a section of code in the source code above for the migration of red and black trees ((TreeNode<K, V>)e). Split (this, newTab, j, oldCap);, Next, let's look at the split() method:
The spit() method transfers the old array to the new array, and the four parameters of the split (HashMap<K, V>map, Node<K, V>[] tab, int index, int bit) method are the current hashMap object, the new array, the old array subscript being traversed, and the length of the old array.
In spit() method, the migration of red and black trees is the same as the migration of the chain table above, with a split process, rehash calculating its index position on the array based on whether (e.hash & bit) equals 0 or not
1. When equal to 0, the index position of the tree chain header node in the new array is equal to its index position in the old array and is recorded as the low-bit tree chain table lo.
2. If it is not equal to 0, the index position of the tree chain header node in the new array is equal to its index position in the old array plus the length of the old array, which is recorded as the high-bit tree chain table hi.
When a red-black tree is split into two small red-black trees, it is turned into a chain table based on the length of the tree.
1. When the number of small red and black tree elements in the low position is less than or equal to 6, the untreeify operation is started.
2. When the number of small red-black tree elements in the low position is greater than 6 and the red-black tree in the high position is not null, the tree operation is started (giving the characteristics of the red-black tree).
See the source notes for the implementation:
// Red-Black Tree Rotation Chain Table Threshold
static final int UNTREEIFY_THRESHOLD = 6;
/**
* @param map HashMap representing expansion
* @param tab Represents a newly created array used to store data migrated from an old array
* @param index Index representing old array
* @param bit Represents the length of an old array and needs to be used in conjunction with bitwise operations
*/
final void split(HashMap<K,V> map, Node<K,V>[] tab, int index, int bit) {
//Make an assignment, because here is ((TreeNode <K, V>) e) where this object calls the split() method, so this is the (TreeNode <K, V>) e object so that the type can correspond to the assignment
TreeNode<K,V> b = this;
//Set low-end and low-end nodes
TreeNode<K,V> loHead = null, loTail = null;
//Set high-end and high-end nodes
TreeNode<K,V> hiHead = null, hiTail = null;
//Defines two variables, lc and hc, with an initial value of 0 and a later comparison, whose size determines whether the red-black tree will go back to the chain table
int lc = 0, hc = 0;
//This for loop is to traverse the entire red and black tree starting from the e node
for (TreeNode<K,V> e = b, next; e != null; e = next) {
//This for loop is to traverse the entire red and black tree starting from the e node
next = (TreeNode<K,V>)e.next;
//After taking the next node of e, assign it to null for GC recycling
e.next = null;
//Distinguish the high and low of the tree chain table, here is the key point of this algorithm as well as the algorithm of the chain table above.
if ((e.hash & bit) == 0) {
//The low tail is marked null to indicate that processing has not started yet, and E is the first low-bit tree chain table node to be processed, so e.prev equals loTail equals null
if ((e.prev = loTail) == null)
//The first tree chain table node of a low-bit tree chain table
loHead = e;
else
loTail.next = e;
loTail = e;
//Count of the number of low-bit tree chain elements
++lc;
}
else {
if ((e.prev = hiTail) == null)
//The first tree chain table node of a high-bit tree chain table
hiHead = e;
else
hiTail.next = e;
hiTail = e;
//Number Count of Elements in High-Bit Tree Chain List
++hc;
}
}
//Low tree chain table is not null
if (loHead != null) {
//Number of low tree chain elements less than or equal to 6
if (lc <= UNTREEIFY_THRESHOLD)
//Begin the de-tree operation (that is, convert all element TreeNode nodes to Node nodes)
tab[index] = loHead.untreeify(map);
else {
tab[index] = loHead;
//If the header node of the high-digit chain is empty, it means that the high-digit chain has not been processed and the tree operation cannot be performed.
if (hiHead != null) // (else is already treeified)
//If the number of low-bit tree chain table elements is greater than 6 and the high-bit tree chain header node is not equal to null, the low-bit tree chain will start to be true
//Ortho-tree into a red-black tree (the name of TreeNode hangs in front of it, but it's actually just a chain structure, not a red-black tree yet.
//It's here that gives it the red and black tree characteristics)
loHead.treeify(tab);
}
}
//High-bit tree chain table is not null
if (hiHead != null) {
//If the number of high-bit tree chain table elements is less than or equal to 6
if (hc <= UNTREEIFY_THRESHOLD)
//Begin the de-tree operation (that is, convert all element TreeNode nodes to Node nodes)
tab[index + bit] = hiHead.untreeify(map);
else {
tab[index + bit] = hiHead;
//If the low-digit chain header node is empty, it means that the low-digit chain has not been processed and the tree operation cannot be performed yet.
if (loHead != null)
//If the number of high-bit tree chain table elements is greater than 6 and the low-bit tree chain head node is not equal to null, the high-bit tree chain table will be truly dendrified into a red-black tree.
hiHead.treeify(tab);
}
}
}
That's the whole HashMap expansion process. It's easy to understand the next put and get methods. My little buddies follow me, and we're almost there.
HashMap insert element (put() method)
put is simple, and the general process is as follows:
- Determine if the array exists or not, initialize (expand)
- Compute hash value to array subscript
- Determine whether there is a collision
No collision, put directly into empty bucket
There is a collision, insert the end of the bucket as a chain table
Determine if the threshold is exceeded, then convert to a red-black tree - Determine if the insert key already exists and replace value if it exists
- Determine if the number of buckets is full, i.e. the array capacity threshold is reached and the capacity is expanded when full
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
// Determines whether an array exists or not, initializes if it does not exist
if ((tab = table) == null || (n = tab.length) == 0)
// The initialization process is expansion, as described above
n = (tab = resize()).length;
// Calculate the hash and determine whether to collide
if ((p = tab[i = (n - 1) & hash]) == null)
// If no collisions are inserted into the new bucket, a new Node is initialized and placed into the table.
tab[i] = newNode(hash, key, value, null);
else { // Create collisions
Node<K,V> e; K k;
// If the key is the same after a collision, this is also a key point. The hash value is the same after a collision, then the key is determined.
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
else if (p instanceof TreeNode) // Determine whether a tree node is a red-black tree structure
// Insert the element into the red-black tree, and after successful insertion e returns null, which is used below e
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else { // Is Chain List
// Traversing a list of chains
for (int binCount = 0; ; ++binCount) {
// It's complicated here, the value of e is p.next, which is used here, but actually it's looking for the end of the list, because to do the tailing, if the following judgment doesn't work, insert the element here
if ((e = p.next) == null) {
// Insert a new node at the end of the list
p.next = newNode(hash, key, value, null);
// Determine whether a threshold has been reached
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
// Convert to Black and Red Tree
treeifyBin(tab, hash);
break;
}
// Here e is p.next above, and each iteration determines if there is a hash, the key address, and the key all have the same value
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
// If the same exists, end the loop directly
break;
p = e;
}
}
// To determine whether e is empty or not, an existing key is inserted, replacing value and returning old value
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
// Determine if capacity expansion is required
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}
HashMap Get Elements (get() method)
Getting elements in HashMap is simpler as follows:
- Determine if an array exists
- Determines if the first element in the array meets the criteria, and returns directly if it meets the criteria
- Determine if there is a collision in the array
Red and Black Trees Get and Return Elements
Loop the list of chains to determine and return elements
See the source notes below for details
public V get(Object key) {
Node<K,V> e;
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
// Determine if the array exists and the hash corresponding to the subscript gets a value that is not null, that is, to have a value in the bucket
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
// Determines if the hash, key memory, and key values of the first element in the bucket are the same, and returns directly if they are the same
if (first.hash == hash && // always check first node
((k = first.key) == key || (key != null && key.equals(k))))
return first;
// If the above condition is not established, there will be a collision
if ((e = first.next) != null) {
// Determine whether it is a red-black tree structure
if (first instanceof TreeNode)
// Find and Return
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
// Circular Chain List
do {
// Determines if the hash value, key memory, and key value of an element are all the same, and returns if they are the same
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
return null;
}
Ending
These are the entire implementation principle of HashMap and the source code parsing. There must be some errors in the above expression. Please wait for your little buddies, and also look forward to them pointing out in the comments that the attitude of being kicked is also a record here based on learning. We will learn from each other and make progress together. Kicked Jun also wishes all your little friends to realize their big factory dream as soon as possible.
That's it. Later in this series, you'll update more about the implementation principles and source code parsing of Java containers to give your little buddies more attention to avoid missing them.