HashMap is a combination of arrays and linked lists. As follows:
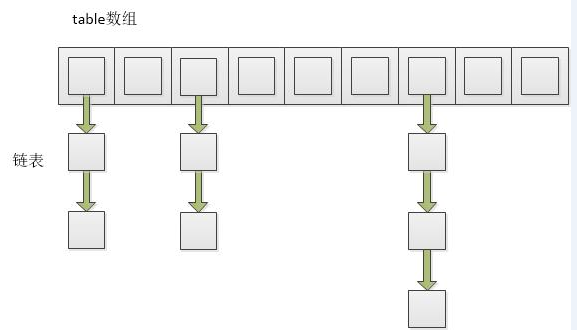
As you can see from the figure, the bottom of HashMap is an array structure, and each array stores a linked list (a reference to the linked list).
JDK 1.6 implements hashmap in the form of bit bucket (array) +linked list, that is, hash linked list. JDK 1.8 adopts the way of bit bucket+linked list/red-black tree, that is, when a bit bucket's linked list length reaches a certain threshold (8), the linked list is transformed into a red-black tree, which greatly reduces the search time.
Storage lookup principle:
- Storage: First get the hashcode of the key, then take the length of the modular array, so as to quickly locate the coordinates to be stored in the array, and then determine whether the elements are stored in the array. If there is no storage, build a new Node node, store Node node in the array, and if there are elements, iterate and then construct a new Node node. The built Node is stored at the end of the list.
- Find: Same as above, get the hashcode of the key, get the coordinates of the elements to be located by taking the length of the module array through hashcode, then iterate the list, compare the equals of keys of each element, and return the element if the same.
When HashMap has the same number of elements, the larger the length of the array, the lower the collision rate of Hash, the higher the efficiency of reading. The smaller the length of the array, the higher the collision rate and the slower the reading speed. Typical example of space changing time.
Next, we analyze the source code of HashMap:
Structural attributes of HashMap:
public class HashMap<K,V> extends AbstractMap<K,V> implements Map<K,V>, Cloneable, Serializable { //Node array for storing data transient Node<K,V>[] table; //Returns the Set view of Map. Entry < K, V > contained in Map. transient Set<Map.Entry<K,V>> entrySet; //Total number of currently stored elements transient int size; //The number of changes in HashMap's internal structure, mainly for fast iteration failures (the following code has the effect of analyzing this variable) transient int modCount; //The next critical value of capacity expansion, size >= threshold, will expand, threshold equals capacity*load factor int threshold; //Loading factor final float loadFactor; //Default Load Factor static final float DEFAULT_LOAD_FACTOR = 0.75f; //Threshold TREEIFY_THRESHOLD Converted from Link List to Red-Black Tree static final int TREEIFY_THRESHOLD = 8; //From the Threshold Conversion Link List of Red-Black Trees to UNTREEIFY_THRESHOLD static final int UNTREEIFY_THRESHOLD = 6; //Default capacity (16) static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16 //Maximum capacity of arrays (1073741824) static final int MAXIMUM_CAPACITY = 1 << 30; //The smallest hash table capacity when bin (elements in the list) in the bucket is denoted. (If this threshold is not reached, that is, hash table capacity is less than MIN_TREEIFY_CAPACITY, and resize expansion is performed when the number of bins in the bucket is too large.) The value of this MIN_TREEIFY_CAPACITY is at least four times that of TREEIFY_THRESHOLD. static final int MIN_TREEIFY_CAPACITY = 64; //Slightly...
Structure of linked list
static class Node<K,V> implements Map.Entry<K,V> { //hash final int hash; final K key; V value; Node<K,V> next; //Slightly...
The Structure of Red-Black Binary Trees
static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> { TreeNode<K,V> parent; // Parent node TreeNode<K,V> left; //Left node TreeNode<K,V> right; //Right node TreeNode<K,V> prev; // needed to unlink next upon deletion boolean red;
HashMap.put (key, value) insertion method
public V put(K key, V value) { return putVal(hash(key), key, value, false, true); } final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) { //p: linked list node n: array length i: index coordinates in the array where the linked list is located Node<K,V>[] tab; Node<K,V> p; int n, i; //Determine whether the tab [] array is empty or the length is equal to 0, and initialize the expansion if ((tab = table) == null || (n = tab.length) == 0) n = (tab = resize()).length; //To determine whether the tab specifies an element at the index location, if not, directly assign the newNode to tab[i] if ((p = tab[i = (n - 1) & hash]) == null) tab[i] = newNode(hash, key, value, null); //If Node exists in the array location else { //The first step is to find the same Node as the key pair to be inserted, which is stored in e, where k is the key of that node. Node<K,V> e; K k; //Determine whether the key already exists (hash and key are equal) if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))) e = p; //If Node is a red-black binary tree, insert the tree else if (p instanceof TreeNode) e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value); //Otherwise, insert the linked list (indicating that the Hash value collided, adding Node to the linked list) else { for (int binCount = 0; ; ++binCount) { //If the node is a tail node, add if ((e = p.next) == null) { p.next = newNode(hash, key, value, null); //If the length of the list is longer than 8, the treeifyBin method is called to determine whether to expand or convert the list into a red-black binary tree. if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st treeifyBin(tab, hash); break; } //If the key exists, exit the loop if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) break; //Execute P as a child of P and start the next loop (p = e = p.next) p = e; } } //In the loop, we judge whether e is null. If null, we add a new node. If not null, we find a Node whose hash and key are identical. if (e != null) { // existing mapping for key V oldValue = e.value; //Determine whether the value value value is updated. (map provides a putIfAbsent method that does not update value if the key exists, but if value==null changes this value in any case) if (!onlyIfAbsent || oldValue == null) e.value = value; //This method is empty and nothing is implemented. Users can overwrite it according to their needs. afterNodeAccess(e); return oldValue; } } //Only when a new node is inserted can + + modCount be performed. ++modCount; //If size > threshold, start expanding (twice as much each time) if (++size > threshold) resize(); //This method is empty and nothing is implemented. Users can overwrite it according to their needs. afterNodeInsertion(evict); return null; }
1. Determine whether the key value is empty or null for the array tab[i], otherwise resize() is performed to expand it.
2. Calculate the array index I that hash is worth inserting according to the key value. If table[i]==null, add new nodes directly and turn to 6. If table[i] is not empty, turn to 3.
3. Judging whether the first element of the list (or binary tree) is the same as key, turning differently to 4, turning equally to 6;
4. Judge whether the first node of the linked list (or binary tree) is treeNode, that is, whether it is a red-black tree, if it is a red-black tree, insert key-value pairs directly into the tree, or not, execute 5.
5. Traverse the linked list to determine whether the length of the linked list is greater than 8 or more, then convert the linked list to a red-black tree (also judge whether the length of the array is less than 64, if less than just expansion, no conversion of the binary tree), insert the operation in the red-black tree, otherwise insert the linked list; Override the value directly; if the putIfAbsent method is called to insert, the value is not updated (only the null element is updated).
6. After successful insertion, determine whether the actual number of size keys exceeds the maximum capacity threshold, and if it exceeds, expand it.
final void treeifyBin(Node<K,V>[] tab, int hash) { int n, index; Node<K,V> e; if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY) resize(); else if ((e = tab[index = (n - 1) & hash]) != null) { TreeNode<K,V> hd = null, tl = null; do { TreeNode<K,V> p = replacementTreeNode(e, null); if (tl == null) hd = p; else { p.prev = tl; tl.next = p; } tl = p; } while ((e = e.next) != null); if ((tab[index] = hd) != null) hd.treeify(tab); } }
1. First, determine whether the length of the array is less than 64, and if it is less than 64, expand it.
2. Otherwise convert the list structure into red-black binary tree structure
The role of modCount variables
public final void forEach(Consumer<? super K> action) { Node<K,V>[] tab; if (action == null) throw new NullPointerException(); if (size > 0 && (tab = table) != null) { int mc = modCount; for (int i = 0; i < tab.length; ++i) { for (Node<K,V> e = tab[i]; e != null; e = e.next) action.accept(e.key); } if (modCount != mc) throw new ConcurrentModificationException(); } }
The function of modCount parameter can be found in the forEast loop. It is when the iterator iterates over the elements in the Map that the elements in the Map cannot be edited (added, deleted, modified). If modified during iteration, a Concurrent ModificationException exception is thrown.
Question Answer:
1. Why not use tab [i = n - 1) & hash]?
It gets the saved bit of the object by (n - 1) & hash, and the length of the underlying array of HashMap is always the n th power of 2, which is the speed optimization of HashMap. When length is always the n-th power of 2, (n-1) & hash operation is equivalent to modularizing length, i.e., h%length, but it is more efficient than% one.
2. Why use red-black binary tree?
Because a good algorithm can not avoid hash collision, can not avoid the situation of too long list, once the list is too long, it will seriously affect the performance of HashMap. JDK8 optimizes HashMap. If the list length exceeds 8, it will be changed to red-black binary tree to improve the speed of access.