hashmap 1.7 capacity expansion occurs before element addition, and 1.8 capacity expansion occurs after element addition
Difference between hashmap 1.7 and 1.8 when adding new elements, 1.7 is added to the head and 1.8 is added to the tail. If it exceeds the preset value, it will turn into a red black tree
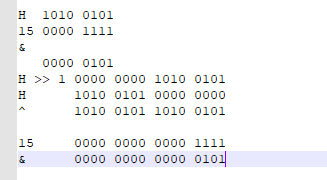
The element subscript calculation of hashmap is to move the hashcode binary of key by one bit to the right, and then XOR the value with the original hashcode, and then sum (&) the value with the array length - 1 in hashmap, so as to obtain the subscript position of the element to be inserted
H 1010 0101
15 0000 1111
&
0000 0101
H >> 1 0000 0000 1010 0101
H 1010 0101 0000 0000
^ 1010 0101 1010 0101
15 0000 0000 0000 1111
& 0000 0000 0000 0101
Note: This is why the length of Hashmap can only take the length of the exponent of 2
Implementation principle: first calculate the hash value of the element key to determine the position inserted into the array, but the elements with the same hash value may have been placed in the same position of the array. At this time, they are added to the back of the elements with the same hash value. They are in the same position of the array, but form a linked list. The hash values on the same linked list are the same, So the array stores a linked list. When the length of the linked list is too long, the linked list will be converted into a red black tree, which greatly improves the efficiency of search
Loading factor (default 0.75): why do I need to use the loading factor and why do I need to expand the capacity?
Because if the fill ratio is very large, it means that a lot of space is used. If the capacity is not expanded all the time, the linked list will become longer and longer, so the search efficiency is very low. Because the length of the linked list is very large (of course, it will be much improved after using the red black tree in the latest version). After the capacity is expanded, Each linked list of the original linked list array is divided into odd and even sub linked lists, which are respectively hung at the hash position of the new linked list array, so as to reduce the length of each linked list and increase the search efficiency
How do HashMap getValue values
public V get(Object key) {
Node<K,V> e;
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
/**
* Implements Map.get and related methods
*
* @param hash hash for key
* @param key the key
* @return the node, or null if none
*/
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab;//Entry object array
Node<K,V> first,e; //The first position hashed in the tab array
int n;
K k;
/*Find the first Node to be inserted by adding hash value and n-1, tab [(n - 1) & hash]*/
//That is, the hash value on a chain is the same
if ((tab = table) != null && (n = tab.length) > 0 &&(first = tab[(n - 1) & hash]) != null) {
/*Check whether the first Node is the Node to be found*/
if (first.hash == hash && // always check first node
((k = first.key) == key || (key != null && key.equals(k))))//The judgment condition is that the hash value should be the same and the key value should be the same
return first;
/*Check the node after first*/
if ((e = first.next) != null) {
if (first instanceof TreeNode)
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
/*Traverse the following linked list to find nodes with the same key value and hash value*/
do {
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
return null;
}
In the get(key) method, get the hash Value of the key, calculate the hash & (n-1) to get the position in the linked list array. First = tab [hash & (n-1)], judge whether the first key is equal to the parameter key, and then traverse the following linked list to find the same key Value and return the corresponding Value
####How to put(key, value) HashMap
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
/**
* Implements Map.put and related methods
*
* @param hash hash for key
* @param key the key
* @param value the value to put
* @param onlyIfAbsent if true, don't change existing value
* @param evict if false, the table is in creation mode.
* @return previous value, or null if none
*/
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab;
Node<K,V> p;
int n, i;
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
/*If the value of table (n-1) & hash is empty, a new node will be created and inserted at this location*/
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
/*Indicates that there is a conflict. Start dealing with the conflict*/
else {
Node<K,V> e;
K k;
/*Check whether the first Node, p, is the value to be found*/
if (p.hash == hash &&((k = p.key) == key || (key != null && key.equals(k))))
e = p;
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
for (int binCount = 0; ; ++binCount) {
/*If the pointer is empty, it will hang behind it*/
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
//If the number of conflicting nodes has reached 8, see whether it is necessary to change the storage structure of the conflicting nodes,
//treeifyBin first judges the length of the current hashMap. If it is less than 64, only
//resize and expand the table. If it reaches 64, the conflicting storage structure will be a red black tree
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
/*If there is the same key value, the traversal ends*/
if (e.hash == hash &&((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
/*That is, there are the same key values on the linked list*/
if (e != null) { // existing mapping for key means that the Value of the key exists
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;//Returns an existing Value
}
}
++modCount;
/*If the current size is greater than the threshold, the threshold is originally the initial capacity * 0.75*/
if (++size > threshold)
resize();//Double expansion
afterNodeInsertion(evict);
return null;
}
##The process of adding key value pair put(key,value) is as follows:
1. Judge whether the key value pair array tab [] is empty or null; otherwise, use the default size resize();
2. Calculate the hash value according to the key value to the inserted array index I. If tab[i]==null, directly create a new node to add, otherwise go to 3
3. Judge whether the method of handling hash conflicts in the current array is linked list or red black tree (check the first node type), and handle them respectively
HasMap's capacity expansion mechanism (resize)
When constructing a hash table, if the initial size is not specified, the default size is 16 (that is, the size of the Node array is 16). If the elements in the Node [] array reach (fill ratio * Node.length), resize the HashMap to twice the original size, which is time-consuming
/**
* Initializes or doubles table size. If null, allocates in
* accord with initial capacity target held in field threshold.
* Otherwise, because we are using power-of-two expansion, the
* elements from each bin must either stay at same index, or move
* with a power of two offset in the new table.
*
* @return the table
*/
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
/*If the length of the old table is not empty*/
if (oldCap > 0) {
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
/*Set the length of the new table to twice the length of the old table, newCap=2*oldCap*/
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
/*Set the threshold of the new table to twice the threshold of the old table, newThr=oldThr*2*/
newThr = oldThr << 1; // double threshold
}
/*If the length of the old table is 0, it means that the table is initialized for the first time*/
else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
else { // zero initial threshold signifies using defaults
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
if (newThr == 0) {
float ft = (float)newCap * loadFactor;//New table length multiplied by load factor
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
/*Let's start to construct a new table and initialize the data in the table*/
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;//Assign new table to table
if (oldTab != null) {//The original table is not empty. Move the data in the original table to the new table
/*Traverse the original old table*/
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
if (e.next == null)//This indicates that this node has no linked list and is directly placed in the e.hash & (newcap - 1) position of the new table
newTab[e.hash & (newCap - 1)] = e;
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
/*If there is a linked list behind e, it means that there is a single linked list behind E. you need to traverse the single linked list and reset each node*/
else { // preserve order
The new calculation is located in the new table and transported
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;//Record the next node
//The capacity of the new table is twice that of the old table. In the instance, the single linked table is divided into two teams,
//e. Hash & oldcap is an even team, and e.hash & oldcap is an odd pair
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {//The lo queue is not null and placed in the original position of the new table
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {//hi queue is not null and placed in the position of j+oldCap in the new table
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
JDK1.8 improvement of using red black tree
The source code of HashMap is optimized in java jdk8. In jdk7, when HashMap deals with "collision", it is stored by linked list. When there are many collision nodes, the query time is O (n).
In jdk8, HashMap adds the data structure of red black tree to deal with "collision". When there are few collision nodes, the linked list storage is used. When there are more than 8 collision nodes, the red black tree (characterized by the query time of O (logn)) storage is used (there is a threshold control, which is greater than the threshold (8), and the linked list storage is converted into red black tree storage)
##Problem analysis:
You may also know that hash collision can have a disastrous impact on the performance of HashMap. If multiple hashCode() values fall into the same bucket, these values are stored in a linked list. In the worst case, all key s are mapped to the same bucket, so the HashMap degenerates into a linked list - the lookup time is from O(1) to O(n).
As the size of HashMap increases, the cost of get() method is also increasing. Since all records are in the super long linked list in the same bucket, it is necessary to traverse half of the list to query an average record.
JDK1. The red black tree of 8hashmap is solved as follows:
If the record in a bucket is too large (currently TREEIFY_THRESHOLD = 8), HashMap will dynamically replace it with a special treemap implementation. The result will be better, O(logn), rather than bad O(n).
How does it work? The records corresponding to the previous conflicting keys are simply appended to a linked list. These records can only be found through traversal. However, after exceeding this threshold, HashMap starts to upgrade the list into a binary tree, using the hash value as the branch variable of the tree. If the two hash values are different but point to the same bucket, the larger one will be inserted into the right subtree. If the hash values are equal, HashMap hopes that the key value should preferably implement the Comparable interface, so that it can be inserted in order. This is not necessary for the key of HashMap, but it is best if it is implemented. If you don't implement this interface, you won't expect performance improvement in case of serious hash collision.