Title Link
Explanation:
Since a block in a graph is a complete graph, there are O(n2)O(n^2)O(n2) edges in the worst case!
However, the edge weights of every complete graph are the same, so the O(n2)O(n^2)O(n2) edges of a complete graph can be subtracted to O(n)O(n)O(n).
Specifically, we can add a new dot in the middle of each complete graph, set the weight of the edge leading to the dot to 0, and set the edge of the dot to the weight of each edge in the original complete graph, so that we can reduce the edge while ensuring that the distance between each point in the complete graph to another point remains unchanged.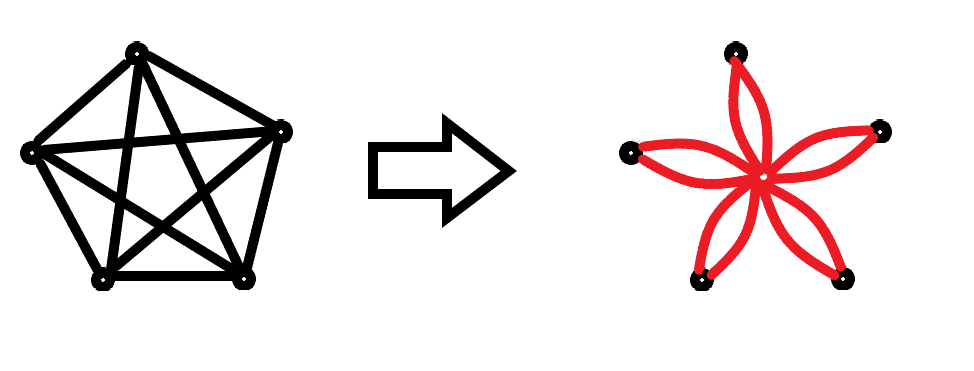

Code:

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef unsigned long long ull;
#define PI acos(-1.0)
#define INF 0x3f3f3f3f3f3f3f3f
#define P pair<ll, int>
#define debug(x) cout << #x << ": " << x << endl
#define fastio ios::sync_with_stdio(false), cin.tie(0)
const int mod = 1e9 + 7;
const int M = 1000000 + 10;
const int N = 200000 + 10;

int t, n, m;
vector<P> G[N];
ll d1[N], dn[N];
int tot;

void dijkstra(int st, ll d[])
{
    for(int i = 1; i <= tot; i ++) d[i] = INF; d[st] = 0;
    bool vis[N] = { false };
    priority_queue<P, vector<P>, greater<P> > que;
    que.push(P{0, st});
    while(que.size()) {
        int now = que.top().second;
        ll dis = que.top().first;
        que.pop();
        if(vis[now]) continue;
        vis[now] = true;
        for(int i = 0; i < G[now].size(); i ++) {
            if(dis + G[now][i].first < d[G[now][i].second]) {
                d[G[now][i].second] = dis + G[now][i].first;
                que.push(P{d[G[now][i].second], G[now][i].second});
            }
        }
    }
}

int main()
{
    scanf("%d", &t);
    for(int cas = 1; cas <= t; cas ++) {
        scanf("%d %d", &n, &m);
        for(int i = 1; i <= n + n; i ++) G[i].clear();
        tot = n;
        for(int i = 1, ti, si; i <= m; i ++) {
            scanf("%d %d", &ti, &si);
            tot ++;
            for(int j = 1; j <= si; j ++) {
                int id;
                scanf("%d", &id);
                G[tot].push_back(P{ti, id});
                G[id].push_back(P{0, tot});
            }
        }

        dijkstra(1, d1);
        if(d1[n] == INF) {
            printf("Case #%d: Evil John\n", cas);
            continue;
        }
        dijkstra(n, dn);

        int ans = INF, node[N], cnt = 0;
        for(int i = 1; i <= n; i ++) {
            if(max(d1[i], dn[i]) < ans) {
                ans = max(d1[i], dn[i]);
                cnt = 0;
                node[++cnt] = i;
            } else if(max(d1[i], dn[i]) == ans) {
                node[++cnt] = i;
            }
        }

        printf("Case #%d: %lld\n", cas, ans);
        for(int i = 1; i <= cnt; i ++) {
            printf("%d%c", node[i], i == cnt ? '\n' : ' ');
        }
    }
    return 0;
}

/*

  Rejoicing in hope, patient in tribulation.

*/