Title original web address: http://acm.hdu.edu.cn/showproblem.php?pid=6183
Title Chinese translation:
Time Limit: 20000/10000 MS (Java/Others) Memory Limit: 132768/132768 K (Java/Others)
Total Submission(s): 1677 Accepted Submission(s): 500
Problem Description
Do you like to paint?Little D doesn't like drawing, especially messy colors.Little B is drawing now.To prevent him from drawing cluttered drawings, Little D asks you to write a program to maintain the following operations.The specific formats for these operations are as follows.
0: Clear all points.
1 x y c: Add a point with the color C at the point (x, y). Note that a point can have many colors and will not be overwritten.
2 x y1 y2: Calculates how many different colors are present in squares (1, y1) and (x, y2).That is, if there is a color point c (a, b), i.e., 1 < a < x and Y1 < B < y2, color c should be calculated.
3: Exit.(
Input
The input contains many lines.
Each row contains one action.It can be'0','1 x y c'(1 < x, y < 106, 0 < c < 50),'2 x y1 y2' (1 < x, y1, Y2 < 106) or'3'.
x, y, c, y1, y2 are integers.
Assuming the last operation is 3, it only occurs once.
The maximum number of consecutive operations in operation 1 and 2 is 15,000.
There are up to 10 operation 0.(
Output
For each operation 2, the output integer represents the answer.(
Sample Input
0
1 1000000 1000000 50
1 1000000 999999 0
1 1000000 999999 0
1 1000000 1000000 49
2 1000000 1000000 1000000
2 1000000 1 1000000
0
1 1 1 1
2 1 1 2
1 1 2 2
2 1 1 2
1 2 2 2
2 1 1 2
1 2 1 3
2 2 1 2
2 10 1 2
2 10 2 2
0
1 1 1 1
2 1 1 1
1 1 2 1
2 1 1 2
1 2 2 1
2 1 1 2
1 2 1 1
2 2 1 2
2 10 1 2
2 10 2 2
3
Sample Output
2
3
1
2
2
3
3
1
1
1
1
1
1
1
Solving ideas:
This question has 50 colors to deal with. It is more troublesome. We might as well consider how to solve it with only one color first.
Because the square we ask for in this question is very special, namely (1, y1) and (x, y2), it means that the square is distributed closely along the y-axis:
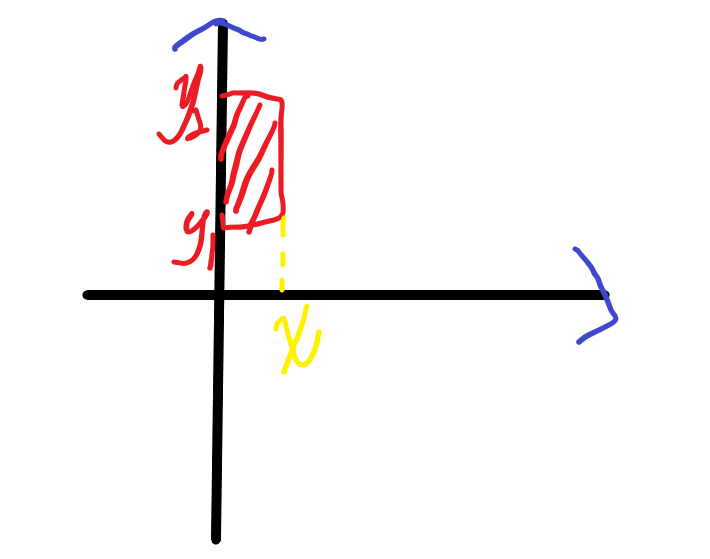
Then we can clearly see that as long as the point's vertical coordinate of this color is between y1 and y2 and its horizontal coordinate is less than x.
Then we maintain a segment tree on the y-axis and record the minimum x value (as long as it is less than x, we only need to record the smallest one).
Back to the point, we have just successfully handled the case of one color. Now let's consider the case of 50 colors.
The easiest thing to think about is maintaining 50 segment trees. Time limits are fine for this topic, but space doesn't meet the requirements, so we're referencing an optimization method
--- Open point segment tree dynamically, its working principle is that whenever I want to use a point to maintain an interval, open up a space for it, I don't open up or visit the points I don't need, just open up twice as much space in advance, which greatly reduces space waste.
AC code:
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 5 using namespace std; 6 7 int noip,noi,root[51],flag; 8 struct kkk { 9 int ls,rs,value;//Because 50 colors are maintained with a segment tree,So you can't use 2 i And 2 i+1 For left and right son 10 kkk() {ls = rs = value = 0;} 11 }e[3000001]; 12 13 void update(int &c,int l,int r,int v,int h) { 14 if(!c) {//If the current point is not opened up,Now open up one 15 c = ++noi; 16 e[c].value = v; 17 } 18 e[c].value = min(e[c].value,v);//Because minimum value is required 19 if(l == r) return ;//If it is a leaf node,Just go back 20 int mid = (l + r) >> 1; 21 if(h <= mid) update(e[c].ls,l,mid,v,h);//Kai Left Son 22 else update(e[c].rs,mid + 1,r,v,h);//Kai Right Son 23 } 24 25 void yin_wei_bu_hui_zhe_ge_de_ying_wen_suo_yi_yong_zhong_wen_jiao_cha_xun(int c,int x,int l,int r,int ll,int rr) { 26 if(flag || !c) return ;//If there is already a point in the square or the point is not opened up,Just go back 27 if(ll <= l && rr >= r) {//If the ordinates meet the requirements 28 if(e[c].value <= x) flag = 1;//Horizontal coordinates meet requirements,Explanation in Square,Mark it 29 return ; 30 } 31 int mid = (l + r) >> 1; 32 if(ll <= mid) yin_wei_bu_hui_zhe_ge_de_ying_wen_suo_yi_yong_zhong_wen_jiao_cha_xun(e[c].ls,x,l,mid,ll,rr); 33 if(rr > mid) yin_wei_bu_hui_zhe_ge_de_ying_wen_suo_yi_yong_zhong_wen_jiao_cha_xun(e[c].rs,x,mid + 1,r,ll,rr); 34 } 35 36 int main() { 37 while(scanf("%d",&noip)) { 38 if(noip == 3) break; 39 if(noip == 0) { 40 for(int i = 1;i <= noi; i++) e[i].ls = e[i].rs = e[i].value = 0; 41 for(int i = 0;i <= 50; i++) memset(root,0,sizeof(root)); 42 noi = 0; 43 } 44 if(noip == 1) { 45 int x,y,c; 46 scanf("%d%d%d",&x,&y,&c); 47 update(root[c],1,1000000,x,y); 48 } 49 if(noip == 2) { 50 int x,x1,y1; 51 scanf("%d%d%d",&x,&x1,&y1); 52 int ans = 0; 53 for(int i = 0;i <= 50; i++) { 54 flag = 0; 55 yin_wei_bu_hui_zhe_ge_de_ying_wen_suo_yi_yong_zhong_wen_jiao_cha_xun(root[i],x,1,1000000,x1,y1); 56 if(flag) ans++; 57 } 58 printf("%d\n",ans); 59 } 60 } 61 return 0; 62 }