This problem uses scan line to get the circumference of rectangle, not including overlapping part. I can scan twice, once vertically, once horizontally, twice. I have written the bug. Now I don't know where the bug is, QAQ. I will write the bug once if I want to.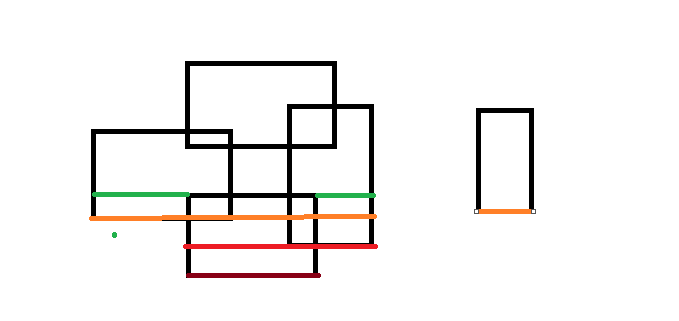

Drawing a picture to simulate the scanning process, we will find that the circumference we cross is the change of the total length of the line segment tree after adding a scanning line, while the vertical one is related to the number of covered sections maintained by our line segment tree. If it is set as X section, then the vertical circumference = (height of the next scanning line - height of this scanning line) * x * 2. So we need to maintain the length of the whole section after adding the scan line, and the length consists of several sections.
Let's talk about maintaining this segment number. For an interval, we need to know how many segments it has. We need to know how many segments its two sons have. Because of the merging of sons, the two segments may be merged into one segment. We maintain two values FL for each interval. Fr indicates whether the left half and companion part of this interval have been covered. If the right part of the left son and the left part of the right son have been covered Part is covered (as follows). Then the number of segments of the father = the sum of the number of segments of the son - 1, the middle part is merged so that the number of segments is less than 1, and other cases = the sum of the number of segments of the son. The final answer is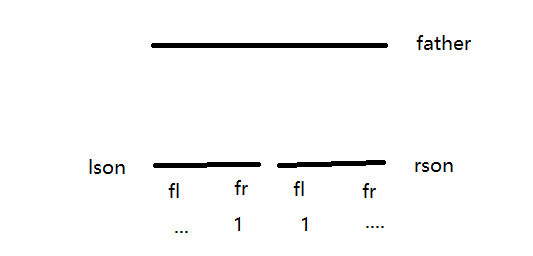

#include<bits/stdc++.h>
#include<iostream>
#include<cstring>
#include<cstdio>
#define mod (10007)
#define middle (l+r)>>1
#define SIZE 1000000+5
#define lowbit(x) (x&(-x))
#define lson (rt<<1)
#define rson (rt<<1|1)
typedef long long ll;
typedef long double ld;
const int inf_max = 0x3f3f3f;
const ll Linf = 9e18;
const int maxn = 2e4 + 5;
const long double E = 2.7182818;
const double eps=0.0001;
using namespace std;
inline int read()
{
    int f=1,res=0;
    char ch=getchar();
    while(ch<'0'||ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
    while(ch>='0'&&ch<='9') { res=res*10+ch-'0' ; ch=getchar(); }
    return f*res;
}
const int up = 100000 + 10;
struct node {
    int l,r,val,h;
    node(){};
    node(int x,int y,int z,int flag) {l = x;r = y;h = z;val = flag;}
}Line[maxn];
struct tnode {
    int flag,segnum,len,fl,fr;
}tree[up << 2];
int n,totx;
bool cmp(node a,node b) {
    return (a.h == b.h ? a.val > b.val : a.h < b.h);
}
void rst() {
    totx = 0;
    memset(tree,0,sizeof(tree));
}
void pushup(int rt,int l,int r) {
    if(tree[rt].flag) { //If the whole range is covered, you don't have to worry about your son, but you will be more shaped
        tree[rt].len = r + 1 - l;
        tree[rt].fl = 1; tree[rt].fr = 1; tree[rt].segnum = 1;
    }else {
        tree[rt].len = tree[lson].len + tree[rson].len;
        tree[rt].segnum = tree[rson].segnum + tree[lson].segnum;
        if(tree[lson].fr == 1 && tree[rson].fl == 1) tree[rt].segnum--; //How to combine the middle part of the left son and the right son
        tree[rt].fl = tree[lson].fl;tree[rt].fr = tree[rson].fr;
    }
}
void update(int rt,int l,int r,int ql,int qr,int f) {
    if(ql == l && qr == r) {
        tree[rt].flag += f;
        pushup(rt,l,r);
        return ;
    }
    int mid = middle;
    if(qr <= mid) update(lson,l,mid,ql,qr,f);
    else if(ql > mid) update(rson,mid + 1,r,ql,qr,f);
    else {
        update(lson,l,mid,ql,mid,f);
        update(rson,mid + 1,r,mid + 1,qr,f);
    }
    pushup(rt,l,r);
}
int main()
{
    while(~scanf("%d",&n)) {
        rst();
        for(int i = 1;i <= n; ++i) {
            int x1,y1,x2,y2;
            scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
            x1 += 10005,y1 += 10005,x2 += 10005,y2 += 10005; //Eliminate discretization
            Line[++totx] = node(x1,x2,y1,1);
            Line[++totx] = node(x1,x2,y2,-1);
        }
        sort(Line + 1,Line + 1 + totx,cmp);
        int ans = 0,pre = 0;
        for(int i = 1;i <= totx; ++i) {
            update(1,1,up,Line[i].l,Line[i].r - 1,Line[i].val); //Change the point to interval, so the right end point should be - 1;
            if(i != totx)
                ans += (2 * tree[1].segnum * (Line[i + 1].h - Line[i].h)); //Calculation vertical
            ans += abs(pre - tree[1].len);//Calculation horizontal
            pre = tree[1].len;
        }
        cout<<ans<<endl;
    }
    return 0;
}