The previous blog post roughly described the implementation of priority queue. This one will talk about heap and heap sorting. For priority queue, please refer to the following blog post. Detailed explanation of binary heap and implementation of priority queue
The above blog post introduces the complete binary tree, full binary tree, heap and heap storage, as well as some implementations of priority queue. This blog post introduces the contents related to heap sorting.
The above provides some common methods, such as the swim method to maintain the characteristics of the heap when inserting an element, and the sink method to maintain the nature of the heap when deleting an element. And some methods, such as left method for left child, right method for right child, and so on
In fact, after understanding the methods related to the swim and sink of the upper heap, it is not difficult to sort the heap. You only need to make a simple transformation.
Another thing to pay attention to is that when the previous blog post introduced priority queue, for the convenience of calculation, the tree heel is stored in the position with subscript 1, as shown in the following figure. This will waste the storage space of a location, but it will be easier to calculate the left node, right node and parent node. Of course, it's the same to start from 0 or 1.
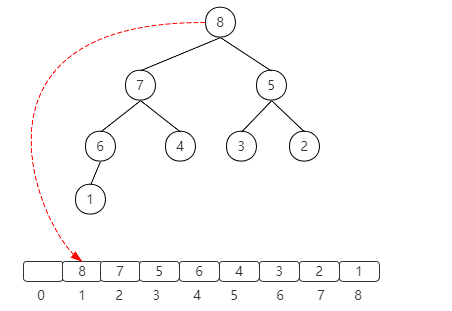
However, heap sorting is generally passed into an array, starting from 0. It is required to sort in place. The tree starts from 0. In fact, the tree root starts from 0
Let's look at the implementation of left, right and parent when the tree root is stored at position 0.
private int left(int index) {
return 2 * index + 1;
}
private int right(int index) {
return 2 * index + 2;
}
private int parent(int index) {
return (index - 1) / 2;
}If the array to be sorted is as follows (note, the default sorting here is ascending)
int[] a = {2, 1, 3, 5, 4, 0, 6, 7}The idea is as follows: a general flow chart is provided here.
Next, let's take a look at how to heap the elements in the array (in place), that is, how to deal with the incoming array to turn it into a binary heap. There are two ways to handle this
Method 1: simulate inserting elements into the heap. After inserting elements, float up to find a suitable position for the newly inserted elements to continue to meet the properties of the heap, as shown in the following array
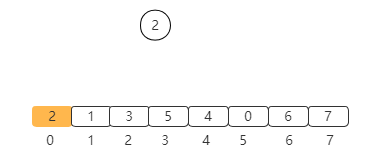
int[] a = {2, 1, 3, 5, 4, 0, 6, 7}All elements are stored in the array, but the tree only reflects some nodes. By default, other nodes are not involved in the construction of the heap, and the insertion will be performed slowly. As shown below, an element must meet the nature of heap and does not need to be heap.
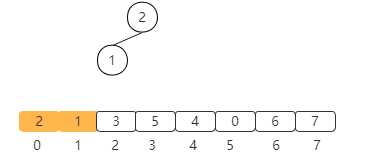
Next, insert the next element 1 into the heap, and maintain the nature of the heap after insertion.
Next, the next element 3 is inserted into the heap to maintain the properties of the heap. After inserting element 3, the properties of the heap are destroyed, and the properties of the heap are maintained through swim
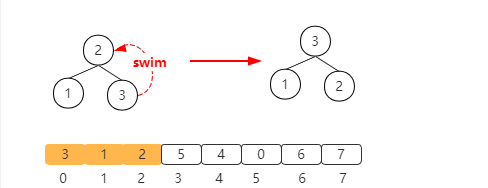
Next, the next element 5 is inserted into the heap to participate in the construction of the heap. After insertion, it needs to float up twice, as shown in the figure below
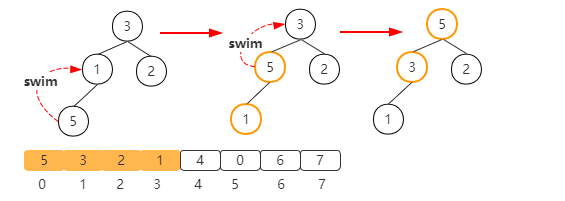
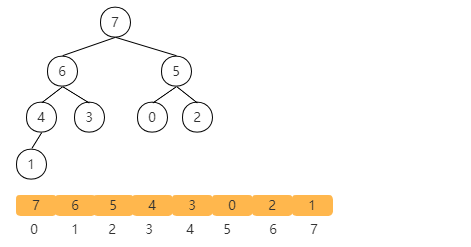
Other elements are similar, as shown in the following figure after heap
After the above analysis, the heap related codes are as follows: some codes are omitted and finally given uniformly
//Heap
private void buildHeap(T[] a, int n) {
//Indicates that the number of elements is less than 1
if (n < 1) return;
for (int i = 1; i <= n; i++) {
swim(a, i);
}
}
/**
* Float up the element at position k to maintain the nature of the maximum heap
*
* @param k
*/
private void swim(T[] a, int k) {
// k> 1 means floating upward until it follows the node
while (k > 0 && less(a, parent(k), k)) {
//Exchange the values of parent and child nodes, and the larger element floats up once
exchange(a, k, parent(k));
//After floating up once, the position that needs to float up also needs to change
k = parent(k);
}
}Method 2. In fact, the heap can be stacked at one time
Or use the following array to illustrate
int[] a = {2, 1, 3, 5, 4, 0, 6, 7}Convert to a complete binary tree, as shown in the following figure
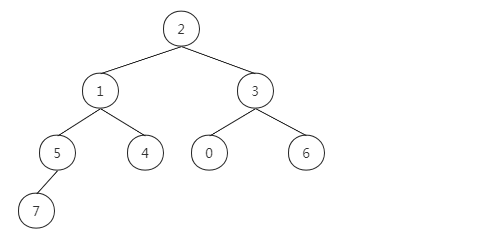
To meet the nature of the large top heap, it only needs that the left node and the right node are not greater than themselves for any node, and the leaf node must meet the nature of the heap, so we only need to traverse the parent node in turn to meet the characteristics of the heap.
How to define the index of the last parent node? We know that for a complete binary tree with n elements, the index of the last node is n - 1 (the index starts from 0), and the index of the parent node is ((n - 1) - 1) /2.
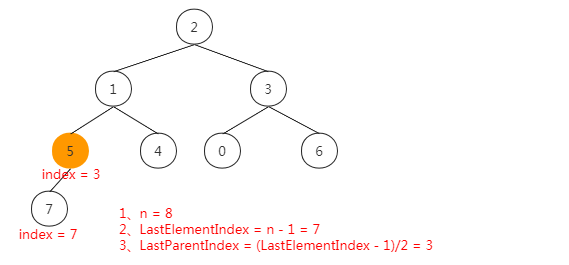
Here, we start from the last parent node. Can we start from the first parent node, that is, the first node? I don't think so. When we heap down, the child nodes do not meet the characteristics of the heap. Therefore, if we want to find the largest node, we can only recursively traverse all nodes. The time complexity will increase, and the nature of reverse heap is different. We can use the previously calculated characteristics. For example, when processing a node, both the left and right nodes have met the characteristics of the heap, Then we can know that the left and right nodes are the maximum of the left and right subtrees.
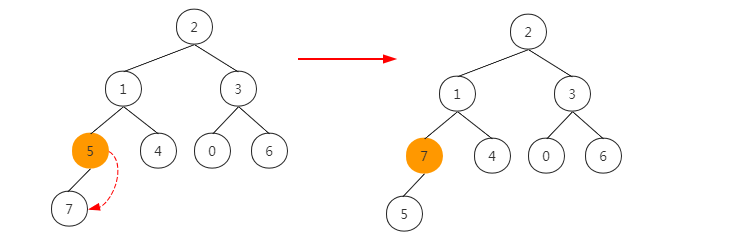
(1) Let's take a look at the heap process through several steps, as shown in the figure below. The last parent node completes heap, that is, the tree with the last parent node as the root meets the characteristics of heap.
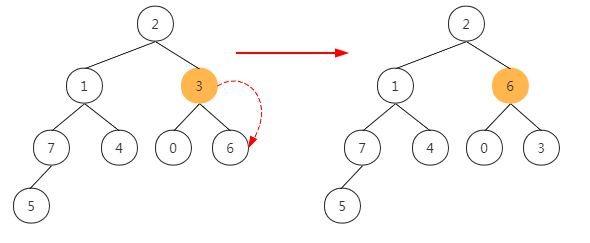
(2) Next, look at the penultimate parent node
(3) The penultimate parent node. Note: element 1 does not meet the characteristics of the heap after sinking once, and must continue to sink
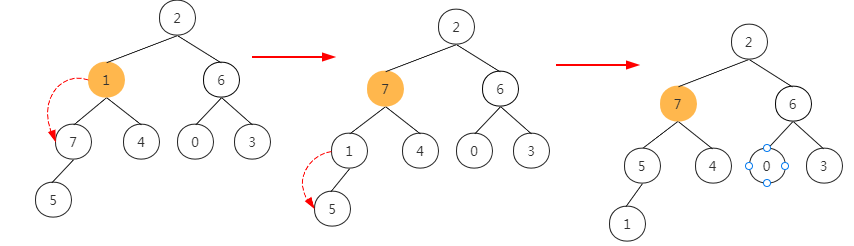
(4) Penultimate parent node
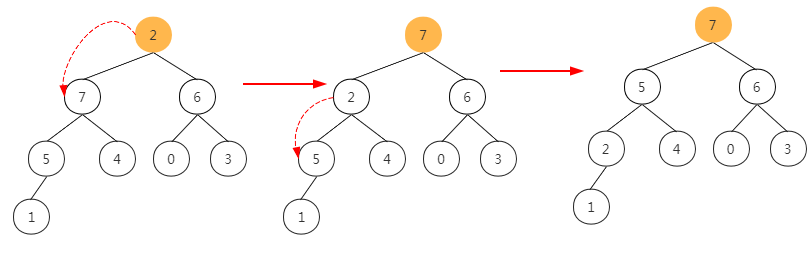
After understanding the principle, the code is relatively simple. The code is as follows (some codes are also omitted here):
private static void buildHeap(int[] a, int n) {
for (int i = (n - 1) / 2; i >= 0; --i) {
heapify(a, n, i);
}
}
private static void heapify(int[] a, int n, int i) {
while (true) {
int maxPos = i;
int leftIndex = left(i);
int rightIndex = right(i);
if (leftIndex <= n && a[i] < a[leftIndex]) maxPos = leftIndex;
if (rightIndex <= n && a[maxPos] < a[rightIndex]) maxPos = rightIndex;
//If equal, there is no need to continue to heap down
if (maxPos == i) break;
//Exchange element
exchange(a, i, maxPos);
//Take the node of max as the new node, and recursively continue to heap down
i = maxPos;
}
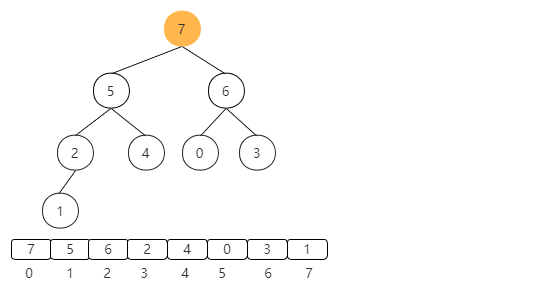
}For the processed heap, see how to handle it to complete the final sorting of the array
After the heap is completed, the largest element (large top heap) has floated up to the root of the tree, that is, to the position of a[0].
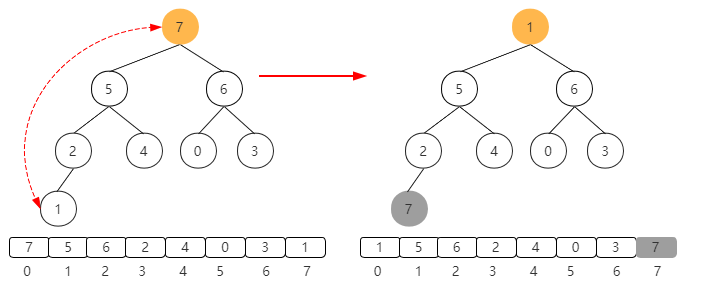
At this time, the first element and the last element are exchanged. After the exchange, as shown in the figure below, this is similar to removing a maximum element from the large top heap. At this time, element 7 can be excluded from the heap and does not participate in the heap processing process. 7 is already the largest element
Because element 1 is moved to the root, it does not meet the characteristics of the large top heap. It needs to sink to complete the heap, as shown in the following figure
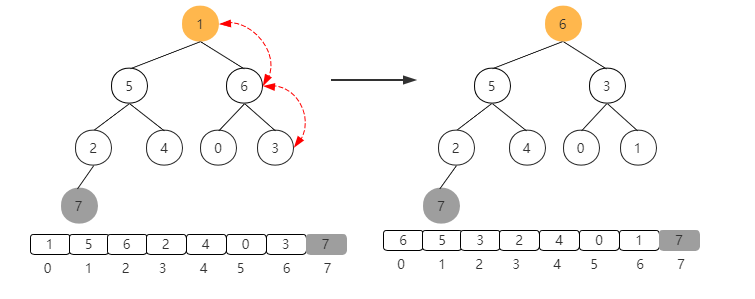
At this time, exchange the elements at the top of the heap with the penultimate one, as shown in the figure below.
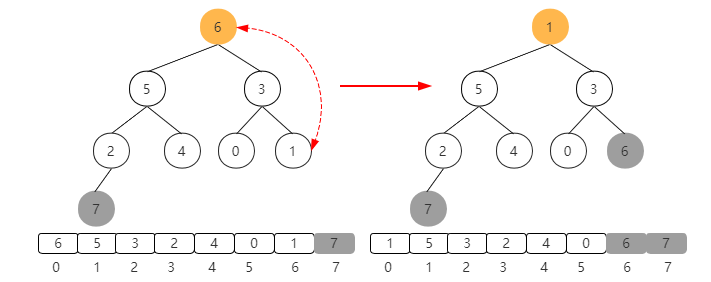
As shown in the figure above, the two largest elements and are successfully sorted to the back of the array. In this way, you know that there is only one element left in the unordered part, as shown in the figure below. At this time, the whole heap is sorted.
After the above analysis, the complete code is as follows:
package com.Ycb.queue;
public class HeapSort<T extends Comparable> {
public void sort(T[] a) {
//n represents the index of the last element of the array
int n = a.length - 1;
int k = n;
buildHeap(a, n);
while (k > 0) {
exchange(a, 0, k);
k--;
sink(a, 0, k);
}
}
//Heap
private void buildHeap(T[] a, int n) {
//Indicates that the number of elements is less than 1
if (n < 1) return;
for (int i = 1; i <= n; i++) {
swim(a, i);
}
}
private void exchange(T[] a, int x, int y) {
T temp = a[x];
a[x] = a[y];
a[y] = temp;
}
private int left(int index) {
return 2 * index + 1;
}
private int right(int index) {
return 2 * index + 2;
}
private int parent(int index) {
return (index - 1) / 2;
}
/**
* Float up the element at position k to maintain the nature of the maximum heap
*
* @param k
*/
private void swim(T[] a, int k) {
// k> 1 means floating upward until it follows the node
while (k > 0 && less(a, parent(k), k)) {
//Exchange the values of parent and child nodes, and the larger element floats up once
exchange(a, k, parent(k));
//After floating up once, the position that needs to float up also needs to change
k = parent(k);
}
}
/**
* Sink the element at position k to maintain the nature of the maximum heap
*
* @param k
*/
private void sink(T[] a, int k, int n) {
//The left node does not exist, indicating that it is a leaf node
while (left(k) <= n) {
//The left node already exists, so it is assumed that the left node is the maximum value
int maxIndex = left(k);
//If the right node exists, compare the size and select the larger node
if (right(k) <= n && less(a, maxIndex, right(k))) {
maxIndex = right(k);
}
//If maxIndex is already smaller than the element where k is located, there is no need to compare it
if (less(a, maxIndex, k)) break;
//Exchange elements of maxIndex and k
exchange(a, maxIndex, k);
//At the same time, set k = maxIndex and continue to sink
k = maxIndex;
}
}
private boolean less(T[] pq, int x, int y) {
return pq[x].compareTo(pq[y]) < 0;
}
}
The time complexity is analyzed below
The time complexity is O (nlgn)
Reference article:
28 | heap and heap sorting: why is heap sorting not as fast as fast sorting?