1, Heap build:

 

 

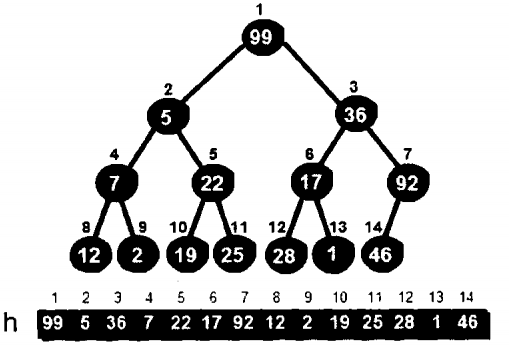
For example, now I want to build this complete binary tree into a heap, as long as each sub tree is the smallest heap. The sub tree is a root node plus two sub nodes.

 

First of all, from the last row, the last row is the leaf node, and the leaf node has no corresponding child nodes. Therefore, all subtrees with the leaf node as the root node meet the characteristics of minimum heap, so they start directly from the upper layer of the leaf node.

 

 

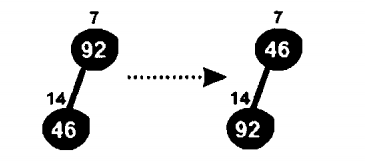
Now look at node 7. It is found that this does not conform to the minimum heap feature, so it is necessary to exchange. The following nodes 4, 5, 6 and 7 carry out the same operation.

 

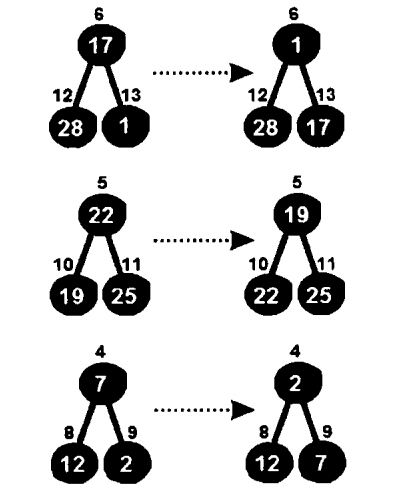
After this layer is exchanged, you will get the following binary tree.

 

 

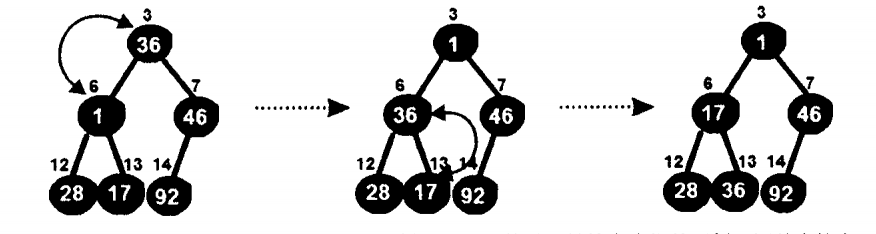
Continue with the same operation on the subtree of the second layer

 

 

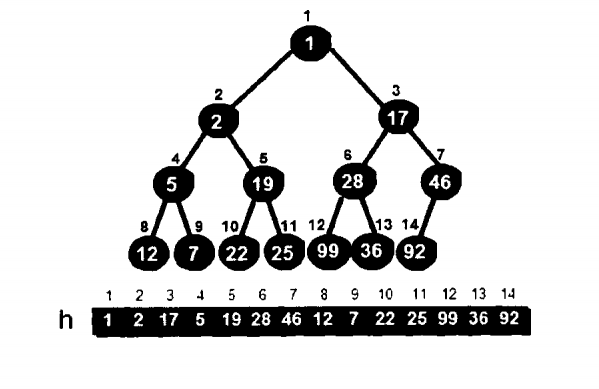
Now you find that you have satisfied the minimum heap feature!

In fact, make a summary: you can get the minimum heap from the previous layer (i = n)) on the leaf node to the first operation above!

for (i = n / 2; i >= 1; i++) {
    siftdown(i);
}

The siftdown function was written in the last blog. In fact, the code is very simple. Just adjust the nodes in these positions upward.

 

2, Heap sort:

In fact, the idea of heap sorting is not difficult. Suppose we want to sort from small to large, we can first establish the minimum heap, and then put the top element into a new array (the top element must be the smallest element in the heap) until the heap is empty. Here is how to delete elements

1 int deletmin() {
2     int  t;
3     t = h[1];//This is the top element
4     h[1] = h[n];
5     n--;
6     siftdown(1);
7     return t;
8 }

 

The idea of this deletion function is to ensure the heap structure. First record the value of the first vertex with a temporary variable, then assign the value of the last element to the first element, and then adjust the element in the first vertex downward. Subtracting the value of n by one is to eliminate the original last element, and finally return the t recorded at the beginning.

 1 #include <bits/stdc++.h>
 2 int h[101];
 3 int n;
 4 using namespace std;
 5 int h[100];
 6 void swap(int a, int b) {
 7     int t;
 8     t = h[a];
 9     h[a] = h[b];
10     h[b] = t;
11     return;
12 }
13 void siftup(int i) {
14     int flag = 0;
15     if (i == 1) {
16         return;
17     }
18     while (i != 1 && flag == 0) {
19         //Judge whether it is smaller than the parent node
20         if (h[i] < h[i / 2]) 
21             swap(i, i / 2);
22         else
23             flag = 1;
24         i = i / 2;
25         
26     }
27     return;
28 }
29 
30 void creat() {
31     int i;
32     for (i = n / 2; i >= 1; i++) {
33         siftdown(i);
34     }
35 }
36 
37 
38 //The following is how to delete the elements in the heap
39 
40 void siftdown(int i) {
41     int t, flag = 0;
42     while (i * 2 < n && flag == 0) {
43         if (h[i] > h[i * 2]) {
44             t = i * 2;
45 
46         }
47         else {
48             t = i;
49         }
50         //In fact, the above is whether it is exchanged with the left node
51         if (i * 2 + 1 <= n) {//That is, there is a right node
52             if (h[t] > h[2 * i + 1]) {
53                 t = 2 * i + 1;
54             }
55         }
56         if (t != i) {
57             swap(t, i);//Pay attention to this swap The function stores the subscript of the array
58             i = t;//The subscript of this place still needs to change
59         }
60         else {
61             flag = 1;
62         }
63     }
64     return;
65 }
66 
67 
68 
69 int deletmin() {
70     int  t;
71     t = h[1];//This is the top element
72     h[1] = h[n];
73     n--;
74     siftdown(1);
75     return t;
76 }
77 
78 int main() {
79     int i,num;
80     scanf("%d", &num);
81     for (int i = 1; i <= num; i++) {
82         scanf("%d", &h[i]);
83     }
84     n = num;
85     //This place n Reassigned
86     creat();
87     for (int i = 1; i <= num; i++) {
88         printf("%d", deletmin());
89 
90     }
91 
92     return 0;
93 }

In fact, there is a simpler method for heap sorting: the previous method is to create a minimum heap, take out the elements at the top of the heap and put them in an array, then put the elements in the last node at the top of the heap, and then adjust downward to maintain the characteristics of the heap. The following method is to create the largest heap. For example, I want to sort from small to large and want the largest to be placed later, so I exchange the first element with the last element. Adjust downward after exchange to ensure the characteristics of the heap.

1 void headsort() {
2     while (n > 1) {
3         swap(1, n);
4         n--;
5         siftdown();
6     }
7     return;
8 }

 

 

Finally, let's make a summary: the data structure that supports inserting elements and finding the largest and smallest elements is called priority queue. If an ordinary queue wants to realize such a function, it is necessary to enumerate the whole queue, so the time complexity is very high.

But I still have a long way to go if I want to learn to use heap sorting and heap to solve problems.

Refer to AHA algorithm