Heap topK problem - heap sorting
The concept of heap ❓
- To represent a binary tree with the child's representation (a common representation for brushing questions) is essentially a chain storage. In fact, there is also a sequential storage for the storage of binary trees. To put it bluntly, take an array to store a binary tree, and the way to fill in the array (starting from 0 subscript) is sequence traversal
- When traversing a complete binary tree in sequence and putting the traversed data into the array, and the value of a node of the binary tree is always not greater than or less than the value of the parent node, the binary tree is a heap
nature 🚶
- If the root of the whole tree is marked as 0, then for a complete binary tree: the subscript of a node is I. if the node has parents, the subscript of its parents is (i-1) / 2
- In a complete binary tree, if the subscript of the parent node is i, if the node has children, the subscript of the left child is 2*i+1 and the subscript of the right child is 2 *i+2
- The heap is physically stored in an array and logically a binary tree
- If all the roots of a complete binary tree are greater than the value of the child nodes around the root, the tree is a large root heap, otherwise it is a small root heap
- The basic function of heap is to find the best value
- The heap in the data frame is the priority queue: PriorityQueue
How to build an array into a heap 🦅
- The essence is to operate an array, so that the elements at the subscript that follow the rules must meet certain requirements, and then the heap building is completed
- There are no more than two kinds of piles, large root pile and small root pile, which determines whether the older children exchange positions with their parents or the smaller children exchange positions with their parents in each binary tree; For example, establish a large root pile: we can take the largest subscript as the last child of the whole tree, and the subscript of the child's parents can be obtained according to property 1, because it is to establish a large root pile to compare the older of the two children with their parents. If the larger one is larger than their parents, exchange the positions of the parents and the older children; When a heap is built on top, the parents at this time may be the children of the next step. The parents at this time are large enough to exchange positions with the parents at the next step. As a result, the elements at the subscript of the parents at this time become smaller, which may make the built bottom binary tree no longer conform to the nature of the heap, so a downward detection step should be added. code:
public class TestDemo {
/*
Adjust the function downward. parent is the root of the tree to be adjusted, and len is the iteration termination condition
*/
private static void shiftDown(int[] array,int parent,int len){
int child=2*parent+1;//Must exist, because the argument is based on the child's parents
while(child<len){
if(child+1<len&&array[child]<array[child+1]){
child++;//Find the older of two children
}
if(array[parent]<array[child]){
swap(array,parent,child);
//After the exchange, it is necessary to detect downward
parent=child;
child=2*parent+1;
}else{
break;//We built it from below to above
}
}
}
private static void swap(int[] array,int i,int j){
int tmp=array[i];
array[i]=array[j];
array[j]=tmp;
}
private static void createBigHeap(int[] array){
for(int parent=(array.length-1-1)/2;parent>=0;parent--){
shiftDown(array,parent,array.length);
}
}
public static void main(String[] args) {
int[] array={1,2,3,4,5,6,7,8,9,10};
createBigHeap(array);
System.out.println("========");
}
}
//Before reactor construction: 1 2 3 4 5 6 7 8 9 10
//After traversing 6 sequences, 2 trees are built into a pile, and 2 trees are indeed built into a pile
Analyze the time complexity of reactor building
Consider the worst case: such as the ascending array in the above code
Restore it into a binary tree by sequence traversal. It can be found that it is a small root pile. When studying a parent every time, it will be found that it needs to be adjusted downward, that is, adjust the elements at the current parent subscript to the lowest level until parent=0; Assuming that the height of the whole tree is k, each node from layer k-1 will be adjusted to the bottom. It can be seen simply that each node of layer k-1 needs to be adjusted down once, each node of layer k-2 needs to be adjusted down twice, and so on: the number of times shiftDown() is executed:
T(N)=2^0 *(K-1)+2^1 *(K-2)+...+2^(K-2) *1
Using dislocation subtraction, we can get T (N) = 2^k-k-1
Another reason is that: for the full binary tree with depth K, the total number of nodes is 2^k -1. The relationship between tree height and node number is deduced: k=log(n+1). The logs here are based on 2
Then: O(n)=2^(log(n+1))-log(n+1)-1=n-log(n+1). Obviously, the latter is not of the same order of magnitude as the former, that is, O(n) is the time complexity
Add an element to the array after the heap is built. How to ensure that the whole is still a heap? 🐰
If you build a large root heap, fill in the new elements with the number of array elements as the subscript to ensure that the whole is still a heap. The essence is to determine where the new elements should be placed, and then the essence is to see how high they can climb? See code:
private static void shiftUp(int[] tmp,int child){
int parent=(child-1)/2;
while(child>0){
if(tmp[child]>tmp[parent]){
swap(tmp,child,parent);
child=parent;
parent=(child-1)/2;
}else{
break;//How high can you climb
}
}
}
private static int[] offer(int[] array,int data){
int[] tmp=new int[array.length+1];
for(int i=0;i<array.length;i++){
tmp[i]=array[i];
}
tmp[array.length]=data;
shiftUp(tmp,tmp.length-1);
return tmp;
}
public static void main(String[] args) {
int[] array={1,2,3,4,5,6,7,8,9,10};
createBigHeap(array);
int[] ret=offer(array,99);
System.out.println("========");
}
How to ensure that the whole heap is still a heap by deleting the elements at the top of the heap 🍊
private static int poll(int[] array){
//First swap the beginning and end elements, and then adjust the 0 lesson tree downward
int tmp=array[0];
swap(array,0,array.length-1);
shiftDown(array,0,array.length-1);
return tmp;
}
topK problem 😋
-
Idea 1: sort the whole, and then take the first k elements, such as bubble sorting with time complexity O(n^2)
-
Idea 2: if the first k maximum values are required, create a small root heap, traverse backward from k+1 elements, and compare these elements with the top elements in turn. If an element is larger than the top element, we can eliminate the top element and put the element into the heap. The operation is to exchange the positions of the two elements, Adjust the whole tree downward. On the contrary, it is not repeated.
Time complexity of analysis idea 2: consider the worst case. If it is an ascending case, find the first k maximum values. After each exchange of the elements at the top of the heap and a subsequent element, the elements at the top of the heap need to be adjusted down to the bottom. The depth of the complete binary tree of the k elements is: log(k+1), from k+1 element to the nth element, Always exchange positions with the opposite top elements, and then adjust them down layer by layer until they reach the bottom layer. Therefore, f(n) = (n-k) * log(k+1-1) is the number of downward adjustments to be made. Exchange is required every time. If it's a big deal, multiply by 2. From the nature of gradual development of big O, we can know that the time complexity of this method is O(n); Space complexity: because it operates on a fixed array and does not involve additional space, the space complexity is O(1)
Code implementation of idea 2:
private static int[] topK(int[] array,int k){
if(array==null) return null;
if(k>array.length) return array;
//The default here is the small root heap, so the first k maximum values are calculated
PriorityQueue<Integer> priorityQueue=new PriorityQueue<>();
for(int i=0;i<k;i++){
priorityQueue.offer(array[i]);//Suppose the first k elements are what we want
}
for(int i=k+1;i<array.length;i++){
int front=priorityQueue.peek();
if(array[i]>front){
priorityQueue.poll();
priorityQueue.offer(array[i]);
}
}
int[] tmp=new int[k];
for(int i=0;i<k;i++){
tmp[i]=priorityQueue.poll();
}
return tmp;
}
public static void main(String[] args) {
int[] array={1,2,3,4,5,6,7,8,9,10};
int[] ret=topK(array,4);
System.out.println(Arrays.toString(ret));
}
Question: what if we want to find the first k smallest elements and build a large root heap?
At this time, the priority queue provides us with a construction method with two parameters:
private static int[] topK(int[] array,int k){
if(array==null) return null;
if(k>array.length) return array;
PriorityQueue<Integer> priorityQueue=new PriorityQueue<>(k, new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2-o1;//Don't write it backwards
}
});
for(int i=0;i<array.length;i++){
if(priorityQueue.size()<k){
priorityQueue.offer(array[i]);
}else{
int front=priorityQueue.peek();
if(front>array[i]){
priorityQueue.poll();
priorityQueue.offer(array[i]);
}
}
}
int[] tmp=new int[k];
for(int i=0;i<k;i++){
tmp[i]=priorityQueue.poll();
}
return tmp;
}
public static void main(String[] args) {
int[] array={1,2,3,4,5,6,7,8,9,10};
int[] ret=topK(array,4);
System.out.println(Arrays.toString(ret));
}
Discussion priority queue 📦
-
If the elements we put in the priority queue are not these numbers here, how can we achieve a "relatively minimum" small root heap at the top of the heap, or vice versa? In this regard, we need to know how to deal with the original code of the priority queue:
The first is nonparametric Construction:
public PriorityQueue() { this(DEFAULT_INITIAL_CAPACITY, null); } //private static final int DEFAULT_INITIAL_CAPACITY = 11; //The null of the latter is actually another field of the priority queue: Private Final comparator <? super E> comparator;According to the usage of this, we can know that although we don't give parameters when using, the bottom layer calls the construction method with two parameters. Let's see:
public PriorityQueue(int initialCapacity, Comparator<? super E> comparator) { // Note: This restriction of at least one is not actually needed, // but continues for 1.5 compatibility if (initialCapacity < 1) throw new IllegalArgumentException(); this.queue = new Object[initialCapacity]; this.comparator = comparator; } //1: An array of 11 capacities is initialized //2: The comparator defaults to null //3: Incidentally, the initial capacity cannot be less than 0At this time, we go to the priority queue: when placing some custom types:
class Card{ public int rank; public String suit; public Card(int rank, String suit) { this.rank = rank; this.suit = suit; } } public class TestDemo{ public static void main(String[] args) { PriorityQueue<Card> priorityQueue=new PriorityQueue<>(); Card card1=new Card(3,"♥"); Card card2=new Card(2,"♠"); priorityQueue.offer(card1); priorityQueue.offer(card2); System.out.println("====="); } } //17 line break points. After debugging, you will find exception in thread "main" Java lang.ClassCastException: Card cannot be cast to java. lang.ComparableThen why does offer () throw this exception? Go to the original code of offer ():
public boolean offer(E e) { if (e == null) throw new NullPointerException(); modCount++; int i = size;//When the size element is placed at 0 if (i >= queue.length) grow(i + 1);//At this time, length is 11 and i is 0, so there is no need to expand the capacity size = i + 1;//The data hasn't been put yet. First increase the size by 1 if (i == 0) queue[0] = e;//The first time we put an element, it is directly placed in the subscript 0. Therefore, if we put only one element in the priority queue, there will be no error else siftUp(i, e);//Put the second element or the third You have to enter the shift up (I, e) return true; }So when we play spade 2, it involves shiftUp(). Go and have a look:
private void siftUp(int k, E x) {//When playing spade 2, here k=1,x is our spade 2 if (comparator != null) siftUpUsingComparator(k, x); else siftUpComparable(k, x);//Enter this }Since our comparator is null by default, enter else:
private void siftUpComparable(int k, E x) { Comparable<? super E> key = (Comparable<? super E>) x; while (k > 0) { int parent = (k - 1) >>> 1;//Find parents according to your son Object e = queue[parent];//Get parent object if (key.compareTo((E) e) >= 0)//Children, that is, our e, that is, our spade 2, call compareTo() to judge whether to enter the if statement according to the size relationship break; queue[k] = e; k = parent; } queue[k] = key; }To sum up, we can see that when the second element of offer() is, an error will be reported, that is, the above-mentioned code in line 16 will make an error first. According to the characteristics of the stack, the first one will be out later, so this error message will be printed finally. The same is true of Debug results.
-
How should we deal with the above problems?
- There are two kinds of object comparison learned before: one is whether the reference of the object is consistent, which is mentioned a lot in the chapter String, and the other is the comparison of some contents of the object itself. In order to solve the above problems, we must give a method for comparison between Card objects
- For the above methods, the first is to implement the Comparable interface of the Card class and rewrite the compareTo function in the Card class; The second is to write a comparator specifically for the Card class, so that offer () has a comparator that can be used when placing the second element or even the following elements
The first is to implement the Card class into a Comparable interface: (e.g. compare only numbers)
class Card implements Comparable<Card>{ public int rank; public String suit; public Card(int rank, String suit) { this.rank = rank; this.suit = suit; } @Override public int compareTo(Card o) { return this.rank-o.rank; } } public class TestDemo{ public static void main(String[] args) { PriorityQueue<Card> priorityQueue=new PriorityQueue<>(); Card card1=new Card(3,"♥"); Card card2=new Card(2,"♠"); priorityQueue.offer(card1); priorityQueue.offer(card2); System.out.println("====="); } }Debug result:
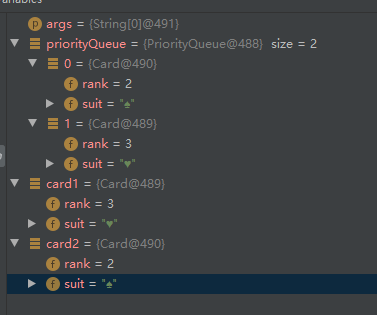
The second card is stored successfully and is a small root heap. If the return value in compareTo() is written in the opposite number, a large root heap will be established!
Second: write a comparator for Card class
class Card{ public int rank; public String suit; public Card(int rank, String suit) { this.rank = rank; this.suit = suit; } } class RankComparator implements Comparator<Card>{ @Override public int compare(Card o1,Card o2){ return o1.rank-o2.rank; } } public class TestDemo{ public static void main(String[] args) { RankComparator rankComparator=new RankComparator(); PriorityQueue<Card> priorityQueue=new PriorityQueue<>(rankComparator); Card card1=new Card(3,"♥"); Card card2=new Card(2,"♠"); priorityQueue.offer(card1); priorityQueue.offer(card2); System.out.println("====="); } }The difference between the above two methods
The first one is too invasive to cards, while the second one has no change to cards.
For the second, we can write it in a special way, so we don't need to write a comparator. The code is as follows:
1: (anonymous inner class)
class Card{ public int rank; public String suit; public Card(int rank, String suit) { this.rank = rank; this.suit = suit; } } public class TestDemo{ public static void main(String[] args) { PriorityQueue<Card> priorityQueue=new PriorityQueue<>(new Comparator<Card>() { @Override public int compare(Card o1, Card o2) { return o2.rank-o1.rank;//This will make the built heap into a large root heap } }); Card card1=new Card(3,"♥"); Card card2=new Card(2,"♠"); priorityQueue.offer(card1); priorityQueue.offer(card2); System.out.println("====="); } }2: lambda expression (poor readability)
class Card{ public int rank; public String suit; public Card(int rank, String suit) { this.rank = rank; this.suit = suit; } } public class TestDemo{ public static void main(String[] args) { PriorityQueue<Card> priorityQueue=new PriorityQueue<>((x,y)->{return x.rank-y.rank;}); Card card1=new Card(3,"♥"); Card card2=new Card(2,"♠"); priorityQueue.offer(card1); priorityQueue.offer(card2); System.out.println("====="); } }