Mangrove black
Red black tree is a binary search tree, but a storage bit is added on each node to represent the color of the node, which can be red or black By limiting the coloring mode of each node on any path from root to leaf node, the red black tree ensures that no path will be twice longer than other paths, so it is close to balance
Properties of red black tree
- Each node is either red or black
- The root node must be black
- If a node is red, its two children are black (there are no consecutive red nodes)
- Starting from a node to all leaf nodes, the number of black nodes passing through is equal
- Each leaf node is black (here leaf node refers to NULL node)
For a node, the shortest path to its leaf node is all black nodes, and the longest path is a black and red staggered path
Implementation of red black tree:
Red black tree node data structure:
enum Color {
Red,
Black
};
template<class T>
struct RBTree {
T _val;
Color _color;
RBTree<T>* _parent;
RBTree<T>* _left;
RBTree<T>* _right;
RBTree(const pair<T>& val = T(), const Color& color = Red)
:_val(val)
,_color(color)
,_parent(nullptr)
,_left(nullptr)
,_right(nullptr)
{}
};Insertion of red black tree:
There are two steps to insert:
- Find the insertion position according to the characteristics of binary search tree
- Adjust according to the characteristics of red and black trees (rotate + adjust color)
Determine the color of the newly inserted node:
If the newly inserted node is red, it may break the rule that there can be no continuous red nodes, and if the inserted node is black, it breaks the rule that the number of black nodes in each path is the same. If it will be damaged, you need to choose a rule that is convenient for repair and cannot have continuous red nodes. You can solve this problem by changing or rotating the color. Therefore, all new nodes are red.
Various situations of inserting nodes:
Case 1: the parent node of the inserted node is black
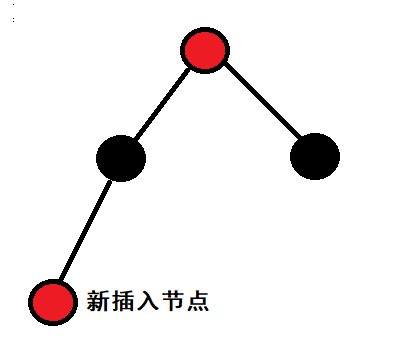
This is the best case, because no rules are broken, so there is no need to deal with it at this time
Case 2: the parent node of the inserted node is red, the uncle node is also red, and the grandfather is black
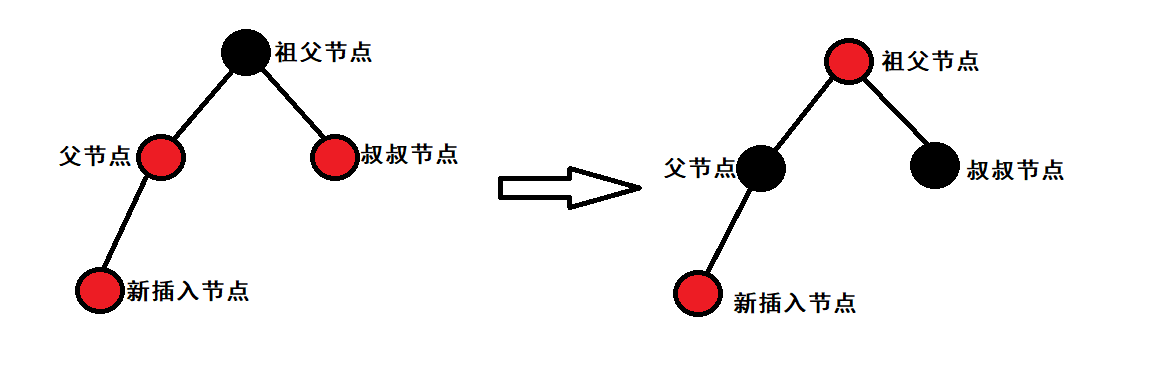
Because there are continuous red nodes, it only needs to correct the color (just turn the parent node and uncle node black and the grandfather node red) At the same time, because there may be other nodes above the grandfather node, it needs to continue to adjust upward from the position of the grandfather node
Case 3: the parent node of the inserted node is red, the uncle is black or does not exist, and the grandfather is black The child is in a straight line with his father
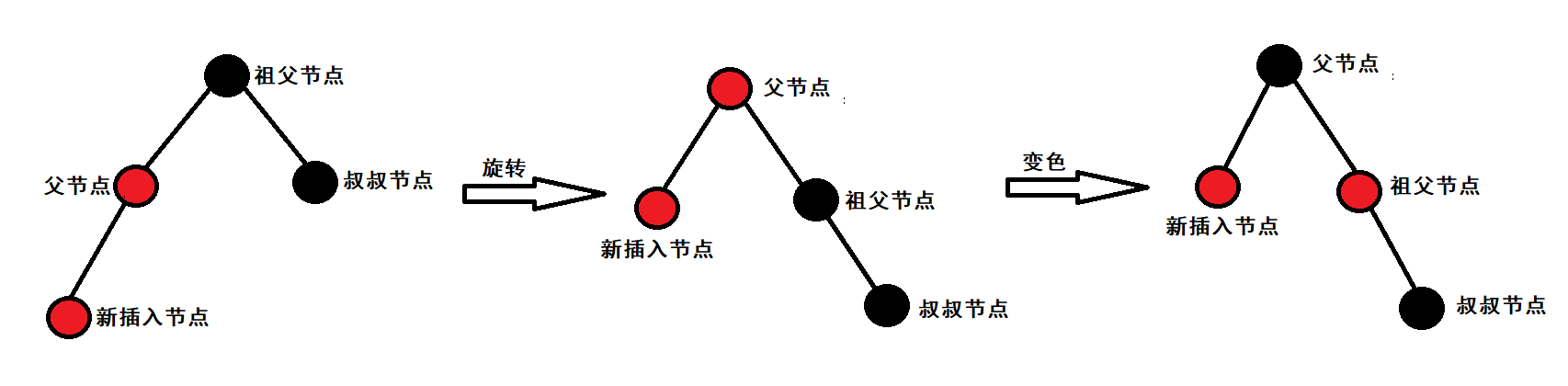
There are two situations:
- If the uncle exists, the child node at this time may be the subtree below. When changing color, it will change from black to red. (otherwise, the same number of black nodes in the path is not satisfied)
- If the uncle does not exist, the child node at this time is the node just inserted in. Because there can be no continuous red nodes, one of the child and the father must be black, but it does not meet the property that the number of black nodes is the same at this time.
The solution is not difficult. It only needs rotation + discoloration
Like the AVL tree, because the father and child are in a straight line, they only need a single rotation.
If the father is the grandfather's left child and the child is the father's left child, the grandfather rotates right
If the father is the grandfather's right child and the child is the father's right child, the grandfather rotates left.
Situation 4: the father is red, the uncle is black or does not exist, and the grandfather is black The child and father are in a state of discount
This situation is similar to situation 3. The solution is double rotation + discoloration
If the father is the grandfather's left child and the child is the father's right child, the father needs left single rotation at this time
If the father is the grandfather's right child and the child is the father's left child, the father needs right single rotation at this time
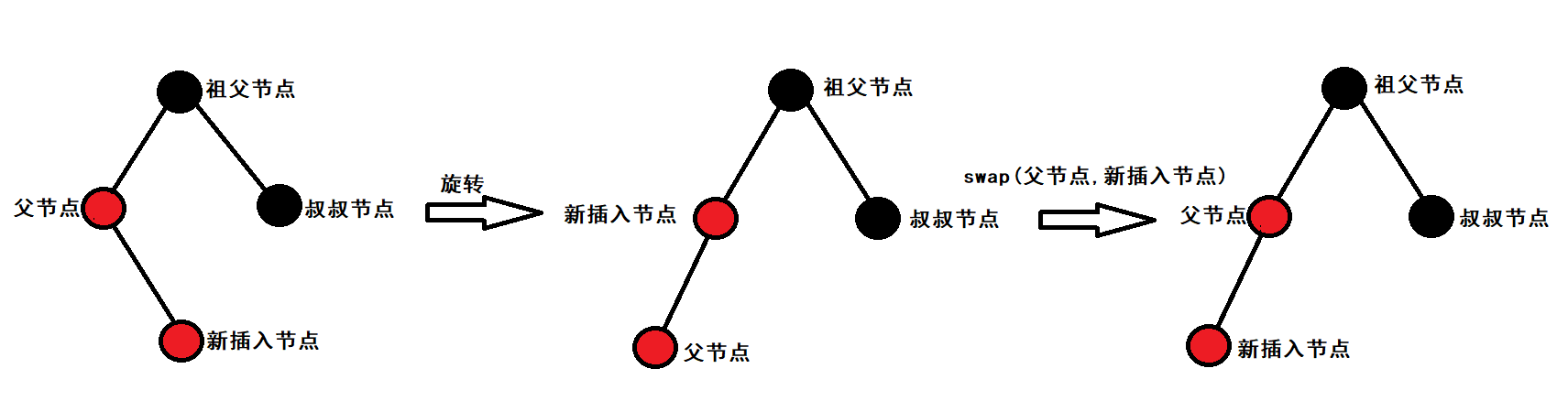After left / right single rotation, after exchanging the parent node and the newly inserted node, it becomes case 3, and then proceed according to the processing method of case 3
bool Insert(const std::pair<K, V>& val){
//Determine whether the tree is empty
if (_root == nullptr){
_root = new Node(val, Black);
return true;
}
//lookup
Node* cur = _root;
Node* parent = nullptr;
while (cur){
if (val.first > cur->_val.first){
parent = cur;
cur = cur->_right;
}
else if (val.first < cur->_val.first){
parent = cur;
cur = cur->_left;
}
else{
return false;
}
}
//The newly inserted node is red
cur = new Node(val, Red);
//Save the inserted node, because the red black tree will be updated up later, so cur may change.
Node* newNode = cur;
//Determine the insertion position
if (cur->_val.first > parent->_val.first){
parent->_right = cur;
}
else{
parent->_left = cur;
}
cur->_parent = parent;
//Update the red black tree. If the color of the parent node is black, it indicates that the conditions are met and need not be processed. If it is red, it indicates that it is not met and need to be processed.
while (parent && parent->_color == Red){
Node* ppNode = parent->_parent;
//If the parent node is the left child tree of the grandfather
if (ppNode->_left == parent){
//At this time, judge the status of the uncle node. The status of the red black tree depends on the uncle
Node* uncle = ppNode->_right;
//In the first case, if the uncle node exists and is red, the father and uncle can be turned black directly, and the grandfather node can be red. Then continue to adjust upward from the position of grandfather
if (uncle && uncle->_color == Red){
//Discoloration
uncle->_color = parent->_color = Black;
ppNode->_color = Red;
//Keep going up
cur = ppNode;
parent = cur->_parent;
}
/*
There are two situations when the uncle node is black or does not exist
Case 2: cur is the left subtree of the parent node, that is, the straight-line state.
Case 3: cur is the right subtree of the parent node, that is, the broken line state.
In case 2, the color can be changed after one single rotation
For case 3, if it is rotated once and then processed slightly, it can be converted to case 2
*/
else{
//Because the double rotation here is different from AVL, the balance factor can not be processed. Therefore, if it is a broken line, it can be rotated first and then converted into a straight line.
//In the third case, the broken line state is converted to the straight line state
if (parent->_right == cur){
RotateL(parent);
//After a single rotation and then exchanging nodes, it can become a straight-line state.
std::swap(parent, cur);
}
//Process the second state
RotateR(ppNode);
parent->_color = Black;
ppNode->_color = Red;
//Processing complete
break;
}
}
//If the father is the right subtree of his grandfather
else{
//At this time, the uncle is the left sub tree.
Node* uncle = ppNode->_left;
if (uncle && uncle->_color == Red){
uncle->_color = parent->_color = Black;
ppNode->_color = Red;
cur = ppNode;
parent = cur->_parent;
}
else{
if (parent->_left == cur){
RotateR(parent);
std::swap(cur, parent);
}
RotateL(ppNode);
ppNode->_color = Red;
parent->_color = Black;
break;
}
}
}
//In order to prevent accidentally changing the root node to red, and finally manually change it to black
_root->_color = Black;
return true;
}
Rotation: left AND right
//Left hand rotation:
void RotateL(){
Node* subR = parent->_right;
Node* subRL = subR->_left;
subR->_left = parent;
parent->_right = subRL;
if(subRL){
subRL->_parent = parent;
}
//Connecting subR to grandfather node
if(parent == _root){
_root = subR;
subR->_parent = nullptr;
}else{
Node* g = parent->_parent;
subR->_parent = g;
if(g->_left == parent){
g->_left = subR;
}else{
g->_right = subR;
}
}
parent->_parent = subR;
}
//Right hand rotation:
void RotateR(Node* parent) {
Node* subL = parent->_left;
Node* subLR = subL->_right;
subL->_right = parent;
parent->_left = subLR;
if (sunLR) {
subLR->_parent = parent;
}
if (parent == root) {
_root = subL;
subL->_parent = nullptr;
}
else {
Node* g = parent->_parent;
subL->_parent = g;
if (g->_left == parent) {
g->_left = subL;
}
else {
g->_right = subL;
}
}
//Then connect the parent's_ parent
parent->_parent = subL;
}
Find:
bool Find(const std::pair<K, V>& data){
//According to the nature of binary search tree, starting from the root node, if it is larger than the root node, find the right subtree, and if it is smaller than the root node, find the left subtree
Node* cur = _root;
while (cur)
{
//If it is larger than the root node, find the right subtree
if (data.first > cur->_data.first)
{
cur = cur->_right;
}
//If it is smaller than the root node, find the left subtree
else if (data.first < cur->_data.first)
{
cur = cur->_left;
}
//Same, return
else
{
return true;
}
}
//After traversal, it indicates that it cannot be found and returns false
return false;
}
Verification of red black tree:
- The root node must be a black node
- There are no continuous red nodes
- Starting from a node to all its leaf nodes, the number of black nodes passing through is equal
bool IsRBTree(){
if (_root == nullptr){
//Empty trees are also red and black trees
return true;
}
//Nature of violation 1
if (_root->_color != BLACK){
return false;
}
//Get the number of black nodes of any sub path starting from the root node, and select the leftmost sub tree here.
Node* cur = _root;
size_t blackCount = 0;
size_t count = 0;
while (cur){
if (cur->_color == BLACK){
blackCount++;
}
cur = cur->_left;
}
//Recursively determine the number of black nodes of other paths
return _IsRBTree(_root, count, blackCount);
}
bool _IsRBTree(Node* root, size_t count, const size_t blackCount){
//At this time, it indicates that you have reached the leaf node to judge whether the number of black nodes is equal. If not, it violates property 3
if (root == nullptr){
if (count != blackCount){
return false;
}
else{
return true;
}
}
//If you haven't finished, then judge other situations
//Judge property 2. If there are continuous red nodes, an error is returned
Node* parent = root->_parent;
if (parent && root->_color == RED && parent->_color == RED){
return false;
}
//If the current node is black, record
if (root->_color == BLACK){
count++;
}
//Then recursively judge all paths of the current node
return _IsRBTree(root->_left, count, blackCount) && _IsRBTree(root->_right, count, blackCount);
}Full code:
#include<iostream>
using namespace std;
enum Color
{
BLACK,
RED,
};
template<class K, class V>
struct RBTreeNode
{
typedef RBTreeNode<K, V> Node;
RBTreeNode(const std::pair<K, V>& data = std::pair<K, V>(), const Color& color = RED)
: _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _data(data)
, _color(color)
{}
Node* _left;
Node* _right;
Node* _parent;
std::pair<K, V> _data;
Color _color;
};
template<class K, class V>
class RBTree
{
public:
typedef RBTreeNode<K, V> Node;
RBTree()
: _root(nullptr)
{}
~RBTree()
{
destory(_root);
}
void _InOrderTravel(Node* root) const
{
if (root == nullptr)
return;
_InOrderTravel(root->_left);
std::cout << root->_data.first << ':' << root->_data.second << std::endl;
_InOrderTravel(root->_right);
}
void InOrderTravel() const
{
_InOrderTravel(_root);
}
void destory(Node*& root)
{
Node* node = root;
if (!root)
return;
destory(node->_left);
destory(node->_right);
delete node;
node = nullptr;
}
//Dextral
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
//If the subLR exists, let its parent node point to the parent.
if (subLR)
{
subLR->_parent = parent;
}
subL->_right = parent;
Node* ppNode = parent->_parent;
parent->_parent = subL;
//Two cases
//If the parent is the root node, make the subL the new root node
if (parent == _root)
{
_root = subL;
subL->_parent = nullptr;
}
//If it is not the root node, change the pointing relationship between the subL and its grandfather node
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subL;
}
else
{
ppNode->_right = subL;
}
subL->_parent = ppNode;
}
}
//Sinistral
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
{
subRL->_parent = parent;
}
subR->_left = parent;
Node* ppNode = parent->_parent;
parent->_parent = subR;
if (parent == _root)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subR;
}
else
{
ppNode->_right = subR;
}
subR->_parent = ppNode;
}
}
bool Find(const std::pair<K, V>& data)
{
//According to the nature of binary search tree, starting from the root node, if it is larger than the root node, find the right subtree, and if it is smaller than the root node, find the left subtree
Node* cur = _root;
while (cur)
{
//If it is larger than the root node, find the right subtree
if (data.first > cur->_data.first)
{
cur = cur->_right;
}
//If it is smaller than the root node, find the left subtree
else if (data.first < cur->_data.first)
{
cur = cur->_left;
}
//Same, return
else
{
return true;
}
}
//After traversal, it indicates that it cannot be found and returns false
return false;
}
bool Insert(const std::pair<K, V>& data)
{
//Find the location first according to the rules of binary search tree
//Create root node
if (_root == nullptr)
{
_root = new Node(data, BLACK);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (data.first > cur->_data.first)
{
parent = cur;
cur = cur->_right;
}
else if (data.first < cur->_data.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
//The newly inserted node is red
cur = new Node(data, RED);
//Save the inserted node, because the red black tree will be updated up later, so cur may change.
Node* newNode = cur;
//Determine the insertion position
if (cur->_data.first > parent->_data.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
//Update the red black tree. If the color of the parent node is black, it indicates that the conditions are met and need not be processed. If it is red, it indicates that it is not met and need to be processed.
while (parent && parent->_color == RED)
{
Node* ppNode = parent->_parent;
//If the parent node is the left child tree of the grandfather
if (ppNode->_left == parent)
{
//At this time, judge the status of the uncle node. The status of the red black tree depends on the uncle
Node* uncle = ppNode->_right;
//In the first case, if the uncle node exists and is red, the father and uncle can be turned black directly, and the grandfather node can be red. Then continue to adjust upward from the position of grandfather
if (uncle && uncle->_color == RED)
{
//Discoloration
uncle->_color = parent->_color = BLACK;
ppNode->_color = RED;
//Keep going up
cur = ppNode;
parent = cur->_parent;
}
/*
There are two situations when the uncle node is black or does not exist
Case 2: cur is the left subtree of the parent node, that is, the straight-line state.
Case 3: cur is the right subtree of the parent node, that is, the broken line state.
In case 2, the color can be changed after one single rotation
For case 3, if it is rotated once and then processed slightly, it can be converted to case 2
*/
else
{
//Because the double rotation here is different from AVL, the balance factor can not be processed. Therefore, if it is a broken line, it can be rotated first and then converted into a straight line.
//In the third case, the broken line state is converted to the straight line state
if (parent->_right == cur)
{
RotateL(parent);
//After a single rotation and then exchanging nodes, it can become a straight-line state.
std::swap(parent, cur);
}
//Process the second state
RotateR(ppNode);
parent->_color = BLACK;
ppNode->_color = RED;
//Processing complete
break;
}
}
//If the father is the right subtree of his grandfather
else
{
//At this time, the uncle is the left sub tree.
Node* uncle = ppNode->_left;
if (uncle && uncle->_color == RED)
{
uncle->_color = parent->_color = BLACK;
ppNode->_color = RED;
cur = ppNode;
parent = cur->_parent;
}
else
{
if (parent->_left == cur)
{
RotateR(parent);
std::swap(cur, parent);
}
RotateL(ppNode);
ppNode->_color = RED;
parent->_color = BLACK;
break;
}
}
}
//In order to prevent accidentally changing the root node to red, and finally manually change it to black
_root->_color = BLACK;
return true;
}