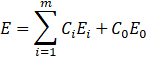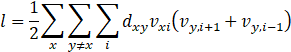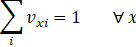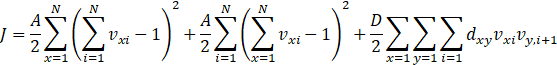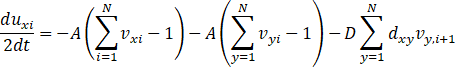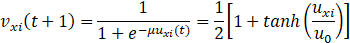catalogue
1, Network principle
Hopfield neural network (HNN) is a fully interconnected feedback neural network, in which each neuron is connected with other neurons.
Hopfield neural network is mainly divided into discrete Hopfield neural network (DHNN) and continuous Hopfield neural network (CHNN). Neurons in discrete Hopfield neural network are quite different from biological neurons because the input and output of biological neurons are continuous and have time delay. Continuous Hopfield neural network is a continuous time neural network model, In this network, the state of neurons can take any real value between 0 and 1. Because the network associative memory process of Hopfield neural network is the process that the nonlinear dynamic system runs towards a stable state. Changing the state of neurons according to the dynamic rules will eventually make the neural network in a stable state.
Discrete Hopfield neural network is a two-state nonlinear dynamic system with multiple input and multiple output generation thresholds. Continuous Hopfield neural network not only simplifies the properties of biological neurons, but also accurately retains the dynamic and nonlinear characteristics of biological neural network. According to its characteristics, discrete Hopfield neural network is usually used to deal with associative memory problems, and continuous Hopfield neural network is usually used to deal with combinatorial optimization problems. TSP problem is a typical combinatorial optimization problem. Therefore, after comprehensive judgment, continuous Hopfield neural network is selected as the algorithm model of this problem.
The key of using neural network to solve the optimization problem is how to map the optimization problem to be solved into a neural network. Generally, each feasible solution of the problem can be expressed by transposition matrix. Another key problem is to construct the energy function so that its minimum value corresponds to the optimal solution of the problem, which determines whether a specific problem can be solved by neural network. Lagrange function and sub multiplication or penalty function method in optimization theory are usually used to construct energy function (formula (1)).
|
| (1) |
Where 
Is a penalty function for violating constraints,
Is the objective function of optimization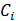
And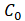
For balance 
and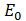 
The proportional constant of the action in the total energy function, and if minimized 
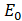, then
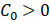； If maximization
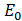, then
；.
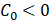In TSP problem, the energy function often reflects the length of the path. If the subscripts x and y represent the city and i represent the ith visit, the path length can be expressed in the following general form:
|
| (2) |
Where
Represents the element in row X and column i of the transposition matrix, and when its value is 1, it means that step i accesses city x, and when its value is 0, it means that step i does not access City X.
In the transposition matrix, only one element in each row and column can be 1, and the rest are 0. Otherwise, it represents an invalid path. Only one element in each column is 1, which means passing through only one city at a time (formula (3)), and only one element in each row is 1, which means passing through each city and only once (formula (4)).
|
| (3) |
|
| (4) |
Using the penalty function method, the above constrained optimization problem is expressed as the following unconstrained optimization problem:
|
| (5) |
At this time, the dynamic equation of Hopfield neural network is:
|
| (6) |
Then = calculated by the first-order Euler method
The input of time is:
|
| (7) |
In order to ensure convergence to the correct solution, that is, only one element in each row and column of transposition matrix V is 1 and the rest is 0, it is calculated by Sigmoid function
.
|
| (8) |
The steady-state solution of the neural network can be obtained by solving the above formula until it converges.
II. Algorithm steps
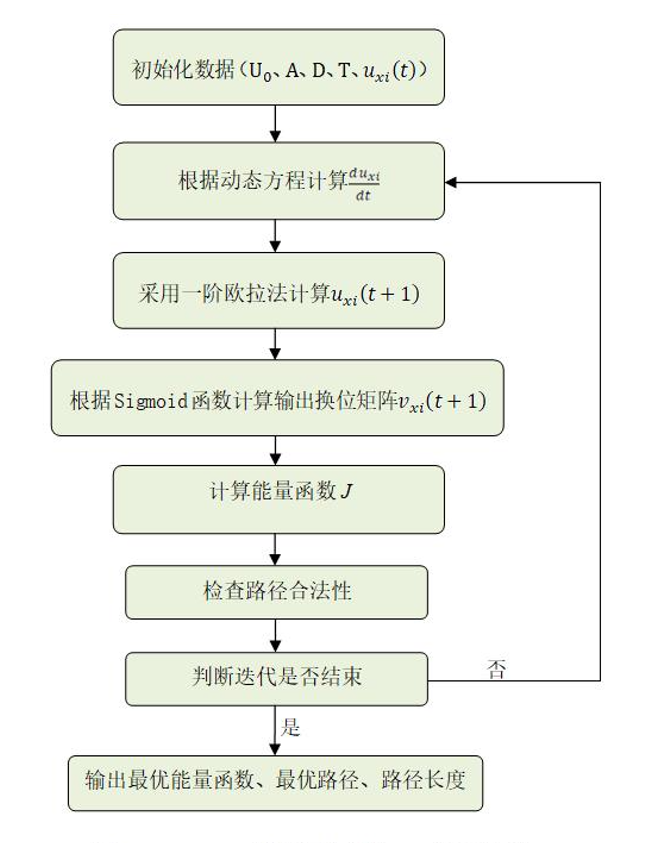
The algorithm steps of Hopfield neural network to solve TSP problem are as follows:
Step 1: set initial value, initial voltage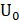
, penalty parameters A and D, number of iterations T;
Step 2: calculate the distance between N cities
；
Step 3: set neural network input near 0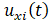 
Initialization value of;
Step 4: calculate according to the dynamic equation (formula (6))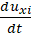
；
Step 5: calculation by first-order Euler method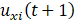
；
Step 6: calculate the output transposition matrix
；
Step 7: calculate the energy function J by applying formula (5);
Step 8: check the validity of the path. Judge whether it ends according to the number of iterations. If it ends, it ends. Otherwise, return to Step 4.
3, Code implementation (Java)
Hopfield class: mainly used for module and interface design
package Hopfield;
import java.io.FileInputStream;
import java.io.IOException;
import java.io.InputStream;
import java.util.ArrayList;
import java.util.List;
import jxl.NumberCell;
import jxl.Sheet;
import jxl.Workbook;
import jxl.read.biff.BiffException;
public class hopfield {
private static final double R = 6371.004;
private int cityNum;//Number of cities
private int MAX;//Number of iterations
//private double bestLength;
private int[] bestTour;
private double[][] distance;//Distance matrix
//private double[][] time;// Time matrix
double[] xx;//Used to output the best path to each city location
double[] yy;//Used to output the best path to each city location
private String filepath;
private double A,D;
private double U0;
//private double[][][][] W;// weight matrix
private double[][] deltaU;//Dynamic results
private double[][] V;//Transposition matrix
private double[][] Ut;//Next moment input
private double[][] U;//Initial value
private double step;//Step size, i.e. delta t
private double E;//Energy value
public hopfield(int MAX,int cityNum,double U0,double step,double A,double D,String filepath) {
this.MAX = MAX;
this.cityNum = cityNum;
this.U0 = U0;
this.step = step;
this.A = A;
this.D = D;
this.filepath = filepath;
bestTour = new int [cityNum];
distance = new double[cityNum][cityNum];
W = new double[cityNum][cityNum][cityNum][cityNum];
V = new double[cityNum][cityNum];
deltaU = new double[cityNum][cityNum];
Ut = new double[cityNum][cityNum];
U = new double[cityNum][cityNum];
xx = new double[cityNum];
yy = new double[cityNum];
}
private static double rad(double d) {
return d * Math.PI / 180.0;
}
//Calculate distance matrix
public double[][] Distance() throws BiffException, IOException{
double[] x = new double[cityNum];
double[] y = new double[cityNum];
distance = new double[cityNum][cityNum];
//Create input stream
InputStream stream = new FileInputStream(filepath);
//Get Excel file object
Workbook rwb = Workbook.getWorkbook(stream);
//Gets the default first of the specified worksheets of the file
Sheet sheet = rwb.getSheet("Sheet2");
for(int i=0;i<sheet.getRows();i++) {
NumberCell cell = null;//It solves the problem that Cell only retains three decimal places
cell = (NumberCell) sheet.getCell(0,i);
x[i] = cell.getValue();
xx[i] = x[i];
cell = (NumberCell) sheet.getCell(1,i);
y[i] = cell.getValue();
yy[i] = y[i];
}
//Calculate the distance between each city
for (int i = 0; i < cityNum - 1; i++) {
distance[i][i] = 0; // Diagonal 0
//Convert latitude and longitude to plane distance
for (int j = i + 1; j < cityNum; j++) {
double rij = 2*R*Math.asin(Math.sqrt(Math.pow(Math.sin((rad(y[j])-rad(y[i]))/2), 2) + Math.cos(rad(y[j]))*Math.cos(rad(y[i]))*Math.pow(Math.sin((rad(x[j])-rad(x[i]))/2), 2)));
distance[i][j] = rij;
distance[j][i] = distance[i][j];
}
}
distance[cityNum - 1][cityNum - 1] = 0;
return distance;
}
//Neural network dynamic equation
public double[][] calc_du(double[][] V,double[][] distance) {
double[] a1 = new double[cityNum];
double[] a2 = new double[cityNum];
double[] b = new double[cityNum];
double[][] t1 = new double[cityNum][cityNum];
double[][] t2 = new double[cityNum][cityNum];
double[][] d = new double[distance.length][V[0].length];
//Add by column
for(int x=0;x<cityNum;x++) {
for(int i=0;i<cityNum;i++) {
a1[x] += V[x][i];
}
}
for(int i=0;i<cityNum;i++) {
for(int j=0;j<cityNum;j++) {
t1[i][j] = a1[j];
}
}
//Add by row
for(int y=0;y<cityNum;y++) {
for(int i=0;i<cityNum;i++) {
a2[i] += V[i][y];
}
}
for(int i=0;i<cityNum;i++) {
for(int j=0;j<cityNum;j++) {
t2[j][i] = a2[j];
}
}
//Place the first column in the last column
for(int i=0;i<cityNum;i++) {
b[i] = V[i][0];
}
for(int i=0;i<cityNum;i++) {
for(int j=0;j<cityNum-1;j++) {
V[i][j] = V[i][j+1];
}
}
for(int i=0;i<cityNum;i++) {
V[i][cityNum-1] = b[i];
}
double sum=0;
for(int j=0;j<V[0].length;j++) {
for(int k=0;k<distance.length;k++) {
for(int i=0;i<distance[0].length;i++) {
sum=sum+distance[k][i]*V[i][j];
}
d[k][j]=sum;
sum=0;
}
}
for(int i=0;i<cityNum;i++) {
for(int j=0;j<cityNum;j++) {
deltaU[i][j] = -1*A*((t1[i][j]-1)+(t2[i][j]-1))-D*d[i][j];
}
}
return deltaU;
}
//Calculated output equation
public double[][] calc_V(double[][] U) {
for(int x=0;x<cityNum;x++) {
for(int i=0;i<cityNum;i++) {
V[x][i] = (1+Math.tanh(U[x][i]/U0))/2;
}
}
return V;
}
//Status update: next moment status Uxi(t0+step)
public double[][] calc_Ut(double[][] deltaU,double[][] U) {
for(int x=0;x<cityNum;x++) {
for(int i=0;i<cityNum;i++) {
Ut[x][i] = deltaU[x][i]*step + U[x][i];
}
}
return Ut;
}
//Energy formula
public double calc_E(double[][] V,double[][] dis) {
double[] a1 = new double[cityNum];
double[] a2 = new double[cityNum];
double[] b = new double[cityNum];
double J;
double t1=0,t2=0,t3=0;
double[][] V1 = new double[cityNum][cityNum];
double[][] d = new double[distance.length][V[0].length];
//Add by column
for(int x=0;x<cityNum;x++) {
for(int i=0;i<cityNum;i++) {
a1[x] += V[x][i];
}
}
for(int i=0;i<cityNum;i++) {
t1 += (a1[i]-1)*(a1[i]-1);
}
//Add by row
for(int y=0;y<cityNum;y++) {
for(int i=0;i<cityNum;i++) {
a2[i] += V[i][y];
}
}
for(int i=0;i<cityNum;i++) {
t2 += (a2[i]-1)*(a2[i]-1);
}
//Place the first column in the last column
for(int i=0;i<cityNum;i++) {
b[i] = V[i][0];
}
for(int i=0;i<cityNum;i++) {
for(int j=0;j<cityNum-1;j++) {
V1[i][j] = V[i][j+1];
}
}
for(int i=0;i<cityNum;i++) {
V1[i][cityNum-1] = b[i];
}
double sum=0;
for(int j=0;j<V[0].length;j++) {
for(int k=0;k<distance.length;k++) {
for(int i=0;i<distance[0].length;i++) {
sum=sum+distance[k][i]*V1[i][j];
}
d[k][j]=sum;
sum=0;
}
}
for(int j=0;j<V[0].length;j++) {
for(int k=0;k<distance.length;k++) {
for(int i=0;i<distance[0].length;i++) {
t3 += d[k][i]*V[i][j];
}
}
}
J = (A*t1+A*t2+D*t3)/2;
return J;
}
public int[] getpath(double[][] V) {
double[] max = new double[cityNum];
//Maximum value per column
for(int j=0;j<cityNum;j++) {
double a=0;
for(int i=0;i<cityNum;i++) {
if(V[i][j] > a) {
a = V[i][j];
}
}
max[j] = a;
//System.out.print(max[j]+",");
}
int j=0;
for(int i=0;i<cityNum;i++) {
if(max[j] == V[i][j]) {
bestTour[j] = i;
j++;
break;
}
}
return bestTour;
}
public static Object[] szqc(int[] a) {
List list = new ArrayList();
//Traversing an array to store elements in a collection
for(int i=0;i<a.length;i++){
//If there is no same element in the collection, it will be saved
if(!list.contains(a[i])){
list.add(a[i]);
}
}
//The toArray() method returns an array of Object types that contains all the elements of the collection
Object[] newArr = list.toArray();
return newArr;
}
public void solve() throws BiffException, IOException {
int tt[] = new int[cityNum];
distance = Distance();
//Initialize Uxi
System.out.println("U");
for(int x=0;x<cityNum;x++) {
for(int i=0;i<cityNum;i++) {
U[x][i] = 1/2*U0*Math.log(cityNum - 1) + (Math.random()*2-1)/10;
System.out.print(U[x][i]+"\t");
}
System.out.println();
}
//Initialize output status
System.out.println("V");
V = calc_V(U);
for(int x=0;x<cityNum;x++) {
for(int i=0;i<cityNum;i++) {
System.out.print(V[x][i]+"\t");
}
System.out.println();
}
//Start iteration
for(int i=0;i<MAX;i++) {
deltaU = calc_du(V,distance);
Ut = calc_Ut(deltaU, U);
U = Ut;
V = calc_V(U);
for(int x=0;x<cityNum;x++) {
for(int i1=0;i1<cityNum;i1++) {
V[x][i1]=Math.round(V[x][i1]);
}
}
E = calc_E(V,distance);
bestTour = getpath(V);
Object[] tour = szqc(bestTour);
if(tour.length == bestTour.length) {
for(int i1=0;i1<cityNum;i1++) {
//int x = bestTour[i];
System.out.print(bestTour[i1]+",");
tt[i1] = bestTour[i1];
}
System.out.println();
double sum1=0;
for(int i1=0;i1<cityNum-1;i1++) {
sum1 +=distance[bestTour[i1]][bestTour[i1+1]];
}
sum1 += distance[bestTour[0]][bestTour[cityNum-1]];
System.out.println("Distance:"+sum1);
System.out.println("E:"+E);
}
}
for(int i=0;i<cityNum;i++) {
System.out.print(tt[i]+",");
}
}
}
hopmain class: calling the launcher
package Hopfield;
import java.io.IOException;
import jxl.read.biff.BiffException;
public class hopmain {
public static void main(String[] args) throws BiffException, IOException {
//Enter the number of iterations, number of cities, U0, step size, A and D parameter values and file path in turn
hopfield hop =new hopfield(50000, 38, 0.02, 0.0001, 1.5, 0.5 ,"D:\\2.xls");
hop.solve();
}
}4, jar package used
jxl package is a special toolkit for reading Excel files. If necessary, you can download it directly on maven's official website.