There are many applications of backtracking. Here's an interesting horse tour problem.

Horse Jumping Day: On an 8*8 chessboard (as shown below), a horse starts at any position, just passes every grid in the chessboard (each grid has and can only walk once), and finally returns to the starting point.

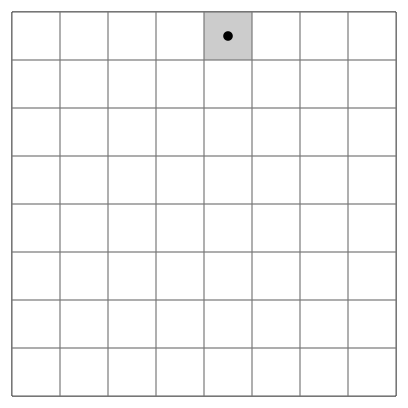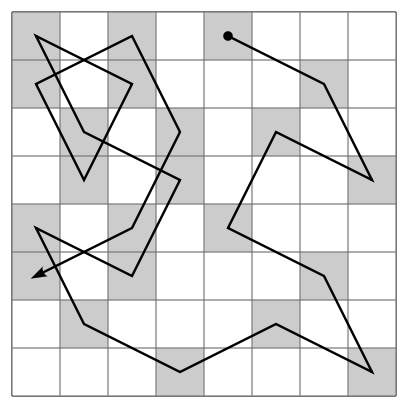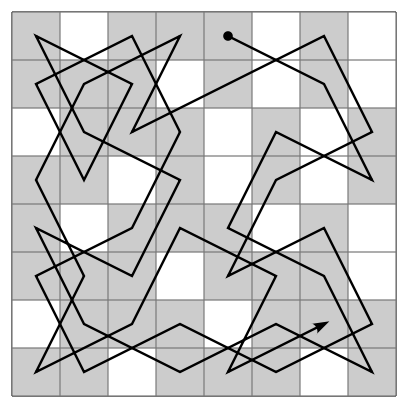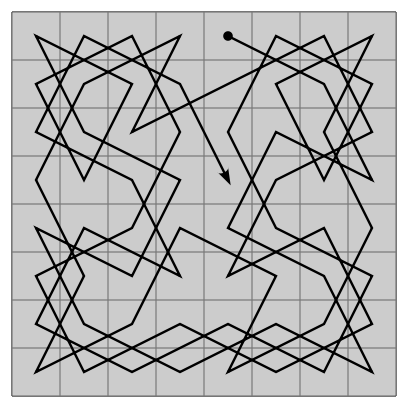
This problem can be generalized: that is, the size of the chessboard is not necessarily 8*8, as long as the size of the chessboard M*N satisfies:

(1) M >= 6; N >= 6; (2) M N is even; (3) | M-N | <=2)

Of course, this problem can also be reduced: that is, the horse does not necessarily return to the origin of the tour, as long as it traverses all the checkerboard grids.

Obviously, the conventional solution is to use the backtracking method, and prune in the process of backtracking.

First, let's start with the simplest description of the horse's travels: that is, the horse's travels only need to go through all the checkerboards, not to return to the starting point.

Solution: In fact, it is easy to understand that a horse travels around the chessboard, that is, to traverse all the lattices on the chessboard once and only once, then it is obviously a problem of traversing a graph. How do you understand it?

In the previous article eight queens Each queen has eight choices of location, which corresponds to the traversal of a full octree (also known as a graph). A diagram of the four queens problem is given below. In this graph, we can clearly see the traversal process of the graph, and depth-first traversal.

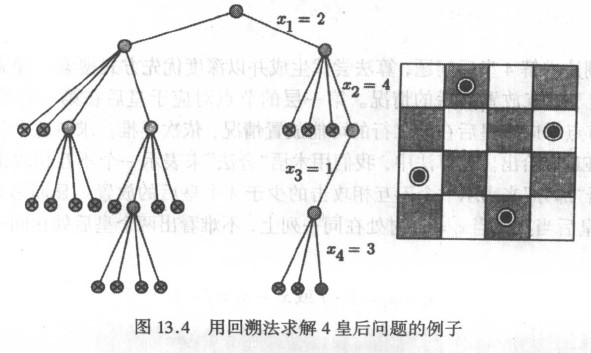
Similarly, the depth-first traversal of a graph is also necessary for horse traveling. Then the depth-first traversal process can be implemented recursively and non-recursively. The following are the actual modern codes.

(1) Recursive implementation

#include<iostream>
#include <stdlib.h>
#include <iomanip>

using namespace std;

//The chessboard of horse's tour should be used from table 1 below.
int board[100][100];

int fx[]= {2,1,-1,-2,-2,-1,1,2};
int fy[]= {-1,-2,-2,-1,1,2,2,1};

int n; //Chessboard size

//The parameters X and Y denote the position of the chessboard
//Testing (x,y) whether the corresponding position is legitimate on the chessboard
bool check(int x,int y)
{
    if(x<1 || y<1 || x>n || y>n || board[x][y] != 0)
        return false;
    return true;
}

//Output results
void outputResult(int n)
{
    for(int i=1; i<=n; i++)
    {
        cout<<endl<<endl;
        for(int j=1; j<=n; j++)
        {
            cout<<setw(3)<<board[i][j]<<" ";
        }
    }
    cout<<endl<<endl;
}

void runTable(int a,int b,int number)
{
    if(number == n*n) //All the points on the chessboard have been completed.
    {
        outputResult(n); //output
        exit(1);
    }

    for(int i=0; i<8; i++) //There are eight ways to walk in each case.
    {
        if(check(a + fx[i],b + fy[i]))
        {
            int x = a + fx[i];
            int y = b + fy[i];

            board[x][y] = number+1; //Go to the next place and set its serial number to number+1

            runTable(x, y,number+1);
            board[x][y] = 0;//To flash back
        }
    }
}

//Recursive Walking Method
void horseRun(int x,int y)
{
    int number = 1;
    board[x][y] = number; //Firstly, the starting position is determined. This lattice is numbered 1.
    runTable(x, y,number);
}

int main()
{
    cout<<"Enter board size n:";
    cin>>n;

    int x,y;
    cout<<"Input the starting position of the horse's circumference x(1~n),y(1~n):";
    cin>>x>>y;

    horseRun(x,y);
    return 0;
}

Operation effect:

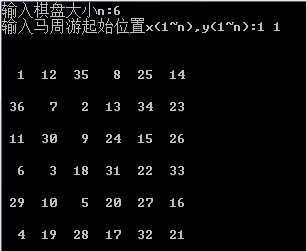
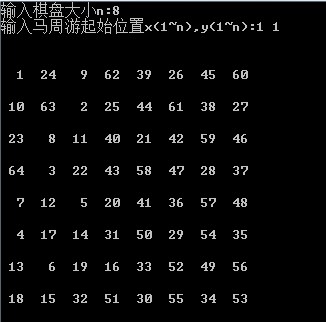
Explanation: When the size of the chessboard is 6*6, the above program can run the result quickly, but when the size of the chessboard is 8*8, it will take several seconds to show that the effect of this operation is not very good.

(2) Non-recursive implementation

#include<iostream>
#include <iomanip>
#include <queue>
using namespace std;

//Eight Ways of Walking in a Lattice
int fx[]= {2,1,-1,-2,-2,-1,1,2};
int fy[]= {-1,-2,-2,-1,1,2,2,1};

typedef struct
{
    int x,y; //coordinate
    int number; //Serial number
} Point; //Lattices on a chessboard

//The chessboard of horse's tour should be used from table 1 below.
Point board[10000][10000];

int n; //Chessboard size
int step =1; //Serial number

//Output results
void outputResult(int n)
{
    for(int i=1; i<=n; i++)
    {
        cout<<endl<<endl;
        for(int j=1; j<=n; j++)
        {
            cout<<setw(3)<<board[i][j].number<<" ";
        }
    }
    cout<<endl<<endl;
}

bool check(int x,int y)
{
    if(x<1 || y<1 || x>n || y>n || board[x][y].number != 0)
        return false;
    return true;
}

//How many ways to walk next?
int nextPosHasSteps(int x, int y)
{
    int steps = 0;
    for (int i = 0; i < 8; ++i)
    {
        if (check(x + fx[i], y + fy[i]))
            steps++;
    }
    return steps;
}

//Non-recursive walking
void horseRun(Point point)
{
    queue<Point> pointQueue;
    pointQueue.push(point);

    Point temp;

    while(!pointQueue.empty())
    {
        temp = pointQueue.front();
        pointQueue.pop();

        board[temp.x][temp.y].number = step++;

        int minStep = 8;

        int flag = 0;

        for(int i=0; i<8; i++) //Entry alignment with the least way out of the next position
        {
            int x=temp.x + fx[i];
            int y=temp.y + fy[i];

            if(check(x,y))
            {
                if(nextPosHasSteps(x,y) <= minStep)
                {
                    minStep = nextPosHasSteps(x,y);

                    Point t;
                    t.x = x;
                    t.y = y;

                    if(flag) pointQueue.pop();

                    pointQueue.push(t);
                    flag = 1;
                }
            }
        }
    }
}

int main()
{
    cout<<"Enter board size n:";
    cin>>n;

    Point startPoint;
    cout<<"Input the starting position of the horse's circumference x(1~n),y(1~n):";
    cin>>startPoint.x>>startPoint.y;

    horseRun(startPoint);
    //Output results
    outputResult(n);
    return 0;
}

Description: In the program has been used a pruning: that is to say, each time the next priority position to walk the least. The details of pruning will be described below.

Operation effect:

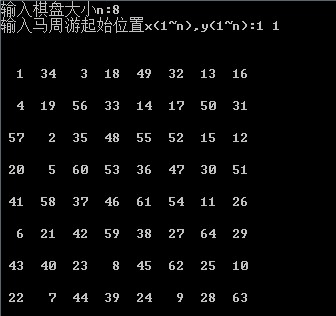
Explanation: This solution can run the result quickly, even in thousands of times thousands of chessboard, almost instantaneously, the effect is very good, because there is a very critical pruning.

2. Complete solution to the problem of horse's traveling: it is necessary to traverse all the checkerboards, and finally return to the starting point.

With the first simplified version of the above horse tour solution experience, then the complete solution to the horse tour problem, can not be added a restriction: finally, to return to the starting point.

First of all, we need to introduce the pruning used in the horse traveling backtracking process (if not pruning, then the efficiency of the algorithm will be very low).

There are three uses of pruning:

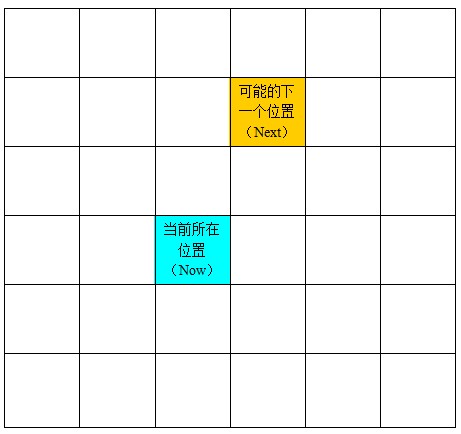
1. Use Warnsdorff's rule s. When considering the next position (Next) in the current position (Now), choose the next position (Next) first and walk the least. As the next position (Next) of the current position (Now).

For example, as shown in the figure below, if the current position is to determine the next position now, then all the next positions should be inspected to see how many ways it can walk in the next position if it goes to the next position. Choose the next position with the least possible way to walk as the next position (Next) of the current position (Now). .

2. After pruning at the first point, if more than one location can be selected as the next priority, the location far from the center will be chosen as the next step (that is, the location near the edge).

Popular point of understanding, the first point of pruning is to take those positions may go to a relatively small opportunity, anyway, the chance to go is small, then it is always good to walk first, or you come back in a circle, or to take this position.

The second point of pruning is to walk as far as possible from the side, and then to the middle.

3. The third point of pruning starts from the middle point of the chessboard every time, and then finds a legal path, then translates and maps back to the path to be found.

How do you understand it? The so-called horse travels around the chessboard, and finally returns to the starting point. That is to find a Hamilton circuit in the chessboard. So no matter where you start, you will end up in this Hamilton circuit, so the location of the selected midpoint must be in this circuit.

Finally, after finding the Hamilton circuit with the midpoint as the starting point, according to the serial number of the starting point in the circuit, map back to the horse's traveling route with this position as the starting point.

Why do we start from the middle of the chessboard? I can't explain much.

Knowing the above three pruning methods, then how to achieve it?

(1) The pruning of the first point and the second point is closely related. Then we can combine the two. When placed in a structure, the structure represents the next position.

typedef struct NextPos
{

    int nextPosSteps; //Indicate how many ways to walk in the next position; Priority for fewer ways to walk
    int nextPosDirection; //The position of the next position relative to the current position
    int nextPosToMidLength; //Represents the distance between the current position and the midpoint; preferences for distances from the midpoint

    //
    bool operator < (const NextPos &a) const
    {
        return nextPosSteps > a.nextPosSteps && nextPosToMidLength < a.nextPosToMidLength;
    }

};

Notice that, The priority of the next position is less walking, and the priority of the next position is far from the midpoint.

So when we select the next position, we can put it in a priority queue that meets the requirements, so that when we select the next position, we can take it out directly from the priority queue (without sorting).

(2) The pruning of the third point is actually related to the final output, which is relatively simple.

The following complete code implementation is given:

#include <iostream>
#include <stdlib.h>
#include <iomanip>
#include <queue>
using namespace std;

typedef struct
{
    int x;
    int y;
} Step;

Step step[8] = { {-2, -1}, {-1, -2}, { 1, -2}, { 2, -1}, { 2, 1}, { 1, 2}, {-1, 2}, {-2,1} };

typedef struct NextPos
{
    int nextPosSteps; //Indicate how many ways to walk in the next position; Priority for fewer ways to walk
    int nextPosDirection; //The position of the next position relative to the current position
    int nextPosToMidLength; //Represents the distance between the current position and the midpoint; preferences for distances from the midpoint

    //
    bool operator < (const NextPos &a) const
    {
        return nextPosSteps > a.nextPosSteps && nextPosToMidLength < a.nextPosToMidLength;
    }

};

int board[100][100];
int M,N; //Chessboard size

//Check if this location is accessible
bool check(int x, int y)
{
    if (x >= 0 && x < M && y >= 0 && y < N && board[x][y] == 0)
        return true;
    return false;
}
//How many ways to walk next?
int nextPosHasSteps(int x, int y)
{
    int steps = 0;
    for (int i = 0; i < 8; ++i)
    {
        if (check(x + step[i].x, y + step[i].y))
            steps++;
    }
    return steps;
}
//Judge whether to go back to the starting point
bool returnStart(int x, int y)
{
    //Check whether you can finally go back to the starting point, that is, the middle position of the chessboard.
    int midx,midy;
    midx = M / 2 - 1;
    midy = N / 2 - 1;
    for (int i = 0; i < 8; ++i)
        if (x + step[i].x == midx && y + step[i].y == midy)
            return true;
    return false;
}

//Output results
void outputResult(int xstart,int ystart)
{
    int num = M * N;
    int k = num - board[xstart][ystart];
    for (int i = 0; i < M; ++i)
    {
        cout<<endl<<endl;
        for (int j = 0; j < N; ++j)
        {
            board[i][j] = (board[i][j] + k) % num + 1;
            cout<<setw(5)<<board[i][j];
        }
    }
    cout<<endl<<endl;
}

//Distance from a position to the center of the chessboard
int posToMidLength(int x,int y)
{
    int midx = M / 2 - 1;
    int midy = N / 2 - 1;
    return (abs(x - midx) + abs(y - midy));
}

void BackTrace(int t, int x, int y,int xstart,int ystart)
{
    //Find the results
    if (t == M * N && returnStart(x,y)) //It traverses all the positions of the chessboard and eventually returns to the starting point to form a loop.
    {
        outputResult(xstart,ystart);
        exit(1);
    }
    else
    {
        priority_queue<NextPos> nextPosQueue;
        for (int i = 0; i < 8; ++i)
        {
            if (check(x + step[i].x, y + step[i].y))
            {
                NextPos aNextPos;
                aNextPos.nextPosSteps = nextPosHasSteps(x + step[i].x, y + step[i].y);
                aNextPos.nextPosDirection = i;
                aNextPos.nextPosToMidLength = posToMidLength(x + step[i].x,y + step[i].y);
                nextPosQueue.push(aNextPos);
            }
        }

        while(nextPosQueue.size())
        {
            int d = nextPosQueue.top().nextPosDirection;
            nextPosQueue.pop();

            x += step[d].x;
            y += step[d].y;
            board[x][y] = t + 1;
            BackTrace(t + 1, x, y,xstart,ystart);
            //To flash back
            board[x][y] = 0;
            x -= step[d].x;
            y -= step[d].y;
        }
    }
}


void horseRun(int xstart,int ystart)
{
    //Initialize the chessboard
    for (int i = 0; i < M; i++)
        for (int j = 0; j < N; j++)
            board[i][j] = 0;
    int midx = M / 2 -1;
    int midy = N / 2 -1;
    board[midx][midy] = 1; //Start the horse's tour from the middle of the chessboard
    BackTrace(1, midx, midy,xstart,ystart);
}

int main(void)
{
    //Starting position of horse Tour
    int x, y;

    cout<<"Please enter the size of the chessboard m*n|m-n|<=2 And m and n Both are even and m,n < 20 :";
    cin>>M>>N;

    cout<<"Please enter the starting position of the horse's Tour--Longitudinal and abscissal coordinates 0 <= x < "<<M<<"And 0 <= y < "<<N<<" :";
    cin>>x>>y;

    horseRun(x,y); //Execute horse Tour
    return 0;
}

Operation effect:

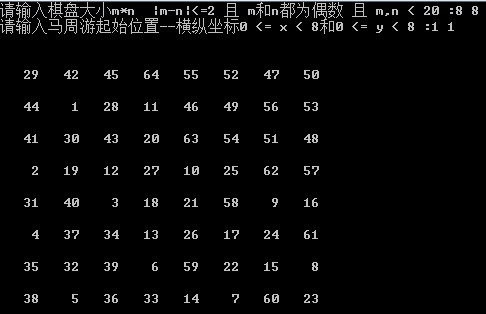
Explanation: The limit of this program is 20, when the size of the chessboard reaches 20 * 20, it is difficult to run out of the results, but the chessboard smaller than 20 can run out of the results quickly.

Well, that's all for the horse tour. Welcome to exchange and discuss.