Reference article: How to replace recursive functions using stack and while-loop to avoid the stack-overflow.
The paper is a foreign literature in full English. Describes some methods of eliminating recursion with stack, after reading, Qui Ji wrote a summary of ~~
First, why use stacks to eliminate recursion? On the one hand, for input with a large amount of data, it can prevent overflow; On the other hand, this approach is closer to nature, and we may be able to write a question easily and recursively, but I think it's also an ability to really write non-recursively.
Of course, the article also mentioned at the end that recursive function is a very clear and concise way of writing. So when writing code, you might want to write recursion first, and eliminate it if necessary.
Returning to the truth and eliminating recursion with stacks is essentially a simulation process. The article makes this process clear, so let me summarize ten rules:
1. Create a structure with three variables: n//input test//local variable stage//state (execution phase)
2. Create a return value variable and initialize the return value to indicate the role of the return function in recursion. (void type can be ignored)
3. Create a stack.
4. Initialize the data and push it onto the stack.
5. Create a loop if the stack is not empty. The structure that will be executed pops up the stack after each loop is executed.
6. This is important because the stages are divided into the call phase and the execution phase after the call returns because the two stages execute different programs. If there are two calls, three states are required. In summary, recursive calls can be divided into different states, since the call is a new block of code.
7. Execute different states according to stages. (Trash.)
8. If a recursive function has a return value, it needs to be stored.
9. Return keywords to write continue in non-recursive functions (as appropriate)
10. Last but not least, the entire algorithm. The step is: If you are performing a recursive function, first change the state of the structure and push it into the stack. Then create a new structure, initialize the data, and push it into the stack.
I would like to explain with my understanding that in a recursive function, if you request a call again, this call is not completed, and the following statements will not be executed until the called function has been executed. At this point in non-recursion, it can be understood that the state has changed, which is why the state has to be pushed onto the stack: the later state will be executed later.
Template code:
int SomeFunc(int n, int &retIdx) //Recursive function
{
...
if(n>0)
{
int test = SomeFunc(n-1, retIdx);
test--;
...
return test;
}
...
return 0;
}
C++
// Conversion to Iterative Function
int SomeFuncLoop(int n, int &retIdx)
{
// (First rule)
struct SnapShotStruct {
int n; // - parameter input
int test; // - local variable that will be local variable within the user function
// after returning from the function call
// - retIdx can be ignored since it is a reference.
int stage; // - Since there is process needed to be done
// after recursive call. (Sixth rule) execution phase
};
// (Second rule)
int retVal = 0; // initialize with default returning value return value variable
// (Third rule)
stack<SnapShotStruct> snapshotStack;
// (Fourth rule)
SnapShotStruct currentSnapshot; //Initialization
currentSnapshot.n= n; // set the value as parameter value
currentSnapshot.test=0; // set the value as default value
currentSnapshot.stage=0; // set the value as initial stage
snapshotStack.push(currentSnapshot);
// (Fifth rule)
while(!snapshotStack.empty())
{
currentSnapshot=snapshotStack.top();
snapshotStack.pop();
// (Sixth rule)
switch( currentSnapshot.stage)
{
case 0: //Call Function Phase
// (Seventh rule)
if( currentSnapshot.n>0 )
{
// (Tenth rule)
currentSnapshot.stage = 1; // - current snapshot need to process after change state
// returning from the recursive call
snapshotStack.push(currentSnapshot); // - This MUST pushed into stack beforeThis call has not finished yet
// new snapshot!
// Create a new snapshot for calling itself
SnapShotStruct newSnapshot;
newSnapshot.n= currentSnapshot.n-1; // - give parameter as parameter given
// when calling itself
// ( SomeFunc(n-1, retIdx) )
newSnapshot.test=0; // - set the value as initial value
newSnapshot.stage=0; // - since it will start from the
// beginning of the function,
// give the initial stage
snapshotStack.push(newSnapshot); //Next call pushed onto the stack
continue;
}
...
// (Eighth rule)
retVal = 0 ;
// (Ninth rule)
continue;
break;
case 1:
// (Seventh rule)
currentSnapshot.test = retVal;
currentSnapshot.test--;
...
// (Eighth rule)
retVal = currentSnapshot.test;
// (Ninth rule)
continue;
break;
}
}
// (Second rule)
return retVal;
}
This is the general method of simulating recursive functions given in this paper. However, this does not mean that every recursive function needs to be simulated as non-recursive. In fact, in most cases, we can do it recursively. For example, factorials, Fibonacci arrays, and most dynamic programming problems can be written recursively, which can be directly converted to recursion, recursively, without using stacks.
Following that line of thought, let me write the Hannotta problem nonrecursively:
Recursive function form:
#include<iostream>
using namespace std;
void move(int n,char x,char y,char z)
{
if(n==1) cout<<x<<"->"<<z<<endl;
else{
move(n-1,x,z,y);
cout<<x<<"->"<<z<<endl;
move(n-1,y,x,z);
}
}
int main()
{
int n;
scanf("%d",&n);
move(n,'A','B','C');
return 0;
}Test run results:
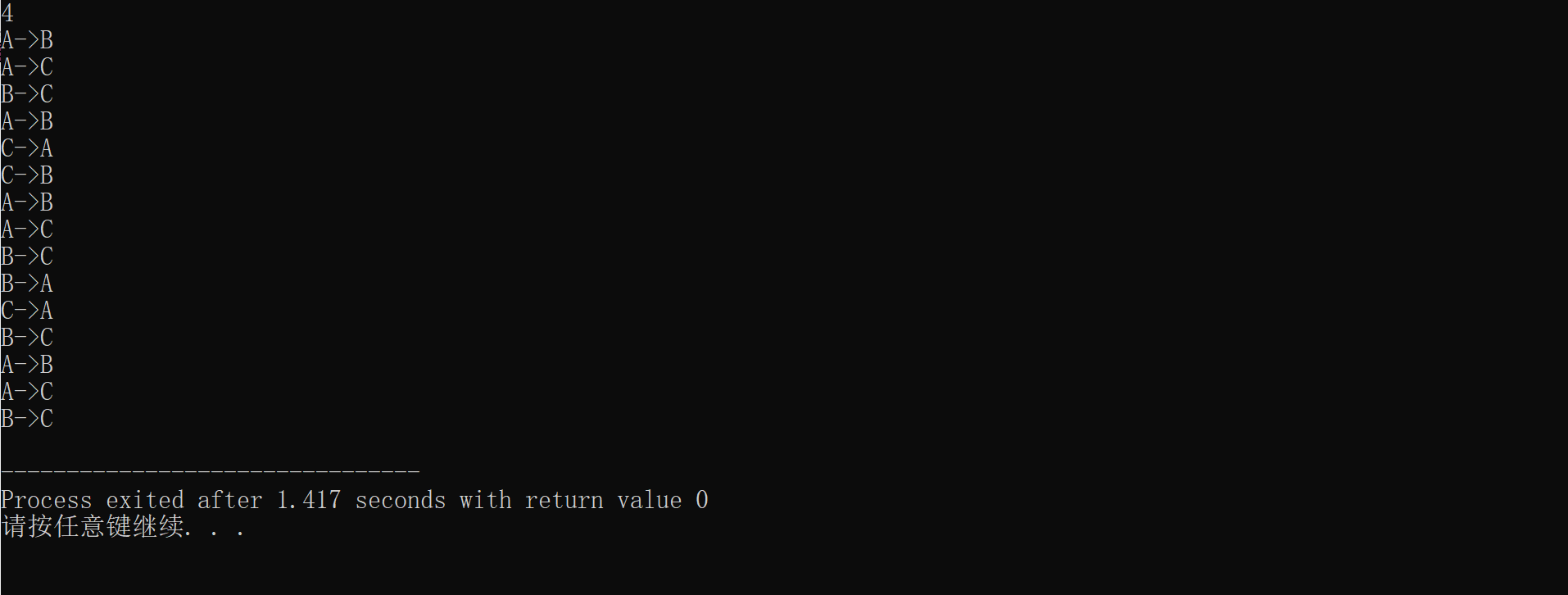
Non-recursive form:
Ideas: A simpler type of simulation, first, the function does not return a value, and does not need to return a value variable. In addition, recursive functions are called twice, so there are three phases.
#include<iostream>
#include<stack>
using namespace std;
struct node{
int n;
char x;
char y;
char z;
int stage; //state variable
};
void move(int n,char x,char y,char z)
{
node currentnode;
currentnode.n=n;
currentnode.x=x;
currentnode.y=y;
currentnode.z=z;
currentnode.stage=0; //Initialization of first call
stack<struct node>S;
S.push(currentnode);
while(!S.empty()){
currentnode=S.top();
S.pop();
switch(currentnode.stage){ //Judgement Status
case 0: //Execute move(n-1,x,z,y);
if(currentnode.n==1) cout<<currentnode.x<<"->"<<currentnode.z<<"\n";
else{
currentnode.stage=1; //Next State
S.push(currentnode); //Remember to push on the stack because the call has not yet been executed
node newnode; //New Call
newnode.n=currentnode.n-1;
newnode.x=currentnode.x;
newnode.y=currentnode.z;
newnode.z=currentnode.y;
newnode.stage=0;
S.push(newnode);
}
break;
case 1:
currentnode.stage=2;
S.push(currentnode); //Same as
cout<<currentnode.x<<"->"<<currentnode.z<<"\n";
break;
case 2: //Execute move(n-1,y,x,z);
if(currentnode.n==1) cout<<currentnode.x<<"->"<<currentnode.z<<"\n";
else{
node newnode; //You have reached the last step without pushing the current onto the stack
newnode.n=currentnode.n-1;
newnode.x=currentnode.y;
newnode.y=currentnode.x;
newnode.z=currentnode.z;
newnode.stage=0;
S.push(newnode);
}
break;
}
}
}
int main()
{
int n;
scanf("%d",&n);
move(n,'A','B','C');
return 0;
}Test run results:
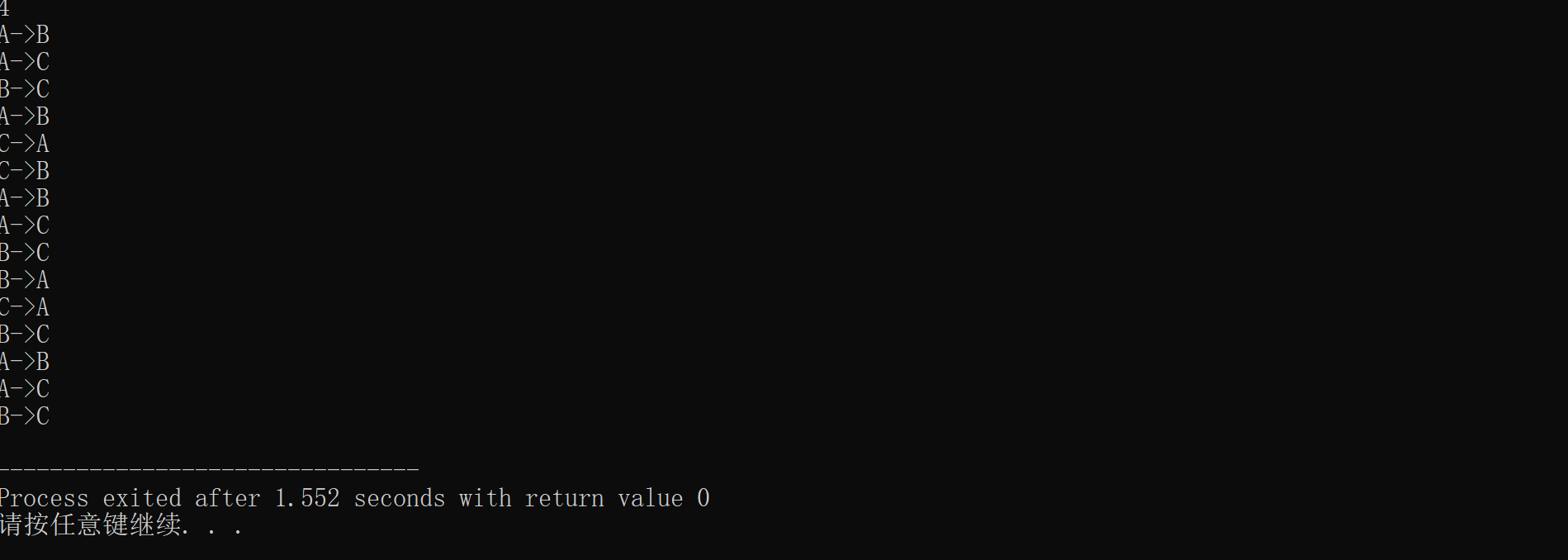
Readers are interested in experimenting with non-recursive writing and arranging, which is not necessarily the case.