How to make Xiaobai write merge sort and reverse order pairs

Xue Chen, Nanfang middle school, Zhuzhou City, Hunan Province

Original address:

https://blog.csdn.net/xuechen_gemgirl/article/details/88654557

 

Yesterday, I shared with Xiaobai the idea of an algorithm for merging, sorting and finding reverse pairs. Generally, Xiaobai doesn't understand the learning of this algorithm. Including my former Xiaobai, it took a lot of effort to understand this algorithm. Then I hope my little white people can learn easily and naturally. Therefore, record it here for future use. (of course, can I use it in the future? I don't know. It is said that the reform of self recruitment will make many children in second and third rate schools unable to learn. I may retire in the future).
[academic analysis] I have an understanding of the execution process of recursive functions, and I basically think about how to write recursion from two aspects: recursive boundary and recursive formula.
[sharing process]
　　１. Write a short program to analyze the impact of the code before recursive function call and the code written after recursion on the program results.
Procedure I

#include<bits/stdc++.h>
using namespace std;
void fun(int n){
	if(n <= 0) return;
	cout << n << endl;
	fun(n-1);
}
int main(){
	fun(5);
	reuturn 0;
}

Procedure II

#include<bits/stdc++.h>
using namespace std;
void fun(int n){
	if(n <= 0) return;	
	fun(n-1);
	cout << n << endl;
}
int main(){
	fun(5);
	reuturn 0;
}

　　

The output of program 1 is output before each recursive call to the next function, which is done before entering a new recursion.
The output of program 2 is output after each recursive call. It is what is done after the recursion comes back.
From the above two programs, it helps to understand the order of things to be done in the recursive process and the position to be placed in the program expression.
２. Try to analyze and solve the problem of two-way merging and sorting.
Given two non descending digital sequences, it is required that the combined digital sequences are still non descending digital sequences. The number of each sequence is 3000000, and each value is between - 109 ~ 109. From the amount of data, adding data to an array will lead to high time complexity of nlogn and the risk of timeout after sorting; According to the range of each value, bucket sorting is unrealistic. Then we need to try a scheme with O (n) time complexity.
Grasping the key point of the order of a given two ordered sequences, we can solve it by two-way merging.

 

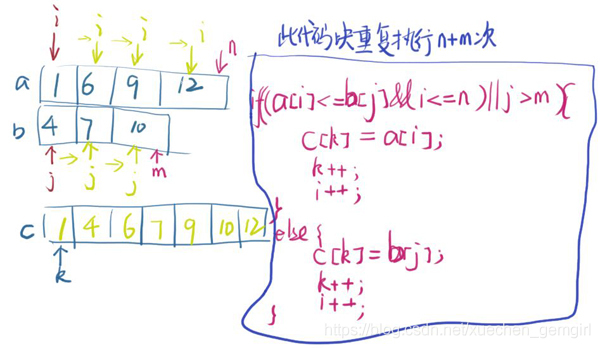
Give about 40 minutes to write the code and write it

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 3000000+1;
int a[MAXN],b[MAXN],c[MAXN*2];
int main(){
	int n,m;
	cin >> n >> m;
	for(int i = 1;i<= n; i++)scanf("%d",&a[i]);
	for(int i = 1;i<= m; i++)scanf("%d",&b[i]);
	for(int k= 1,i = 1,j = 1;k<= n + m; k++){
		if((a[i] <= b[j]&& i<= n)|| j > m ){
			c[k] = a[i];
			i++;
		}else{
			c[k] = b[j];
			j++;
		}
		printf("%d ",c[k]);
	}
	return 0;
}

　　

3. Analyze the problem of reverse order.
In two-way merging, suppose that two sequences are arranged side by side, with array a in the front and array b in the back. How many reverse pairs exist in such a sequence? It is analyzed that when b[j] is placed, it is because a[i] is larger than it that b[j] is placed in c[k]. Then the number of subscripts from i ~n in the current a array is greater than the current b[j], so it can produce an inverse pair n-i+1 pair. In turn, when each b[j] is put into the c array, count the number of reverse pairs that can be generated at present. In this way, the cumulative number is the number of reverse pairs in the array after splicing, and it is also merged into an orderly state.
However, not every array can be ordered in the left and right parts at a given time, so it cannot be operated in this way. So how can we create conditions to make it orderly and meet this condition, and calculate it in reverse order?
Assuming that the data required to find the reverse order pair is a[1] to a[n], it is required to solve the problems of ordered state and reverse order pair of a[1]~a[(1+n)/2] sequence and ordered state and reverse order pair of a[(1+n)/2] to a[n] sequence. We will find that in this process, the problem has not changed, but the scale of the problem is shrinking. For such problems, we can use recursive writing. When the recursion reaches only one number, it will stop dividing. When there is only one number on the left and right, it can be regarded as the merging of two ordered sequences. Therefore, after dividing, it will start the two-way merging of the two parts of the current sequence, and count the number of pairs in reverse order. So recursion is:

 

 

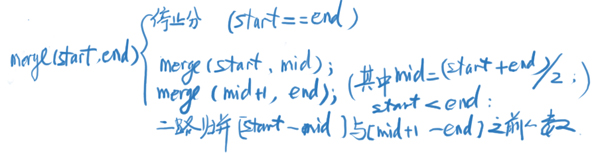
Then a set of numbers is used to simulate the process of opening and closing

 

 

The blue note is the process of recursion, and the red note is the process of recursion. Carefully observe that in order to order the original array, the ordered contents are merged into an auxiliary array during two-way merging. Therefore, after merging, it is necessary to cover the ordered values in the auxiliary array back to the space corresponding to the original array.
See code for details:

void mergesort(int left,int right){
	if(left == right) return;
	int mid = (left + right) / 2;
	mergesort(left, mid);    //branch
	mergesort(mid+1 , right);//branch
	// Two way merging
	int i = left,j = mid+1;
	for(int k = left ;k <= right; k++){
		if((a[i] <= a[j] && i<=mid) || j>right){
			tmp[k] = a[i];
			i++;
		} 
		else{
			ans += mid - i + 1;  //Count the number of pairs in reverse order.
			tmp[k] = a[j];
			j++;
		}
	} 
	for(int k = left; k <= right; k++){   //Put the ordered values in the auxiliary array back into the original array a.
		a[k] = tmp[k];
	}
}

In this way, not only the order is arranged, but also the number of reverse order pairs is counted.