JS implementation of various sorting

There are many kinds of sorting in data structure algorithms, common and uncommon, including at least ten kinds. According to their characteristics, they can be roughly divided into two types: comparison sort and non comparison sort.

Comparison sort: the relative order between elements is determined by comparison, and its time complexity cannot exceed O(nlogn), so it is also called nonlinear time comparison sort.

Non comparison sort: the relative order between elements is not determined by comparison. It can break through the lower bound of time based on comparison sort and run in linear time. Therefore, it is also called linear time non comparison sort.

Let's take a picture to see which sorting methods are included in the two classification methods.

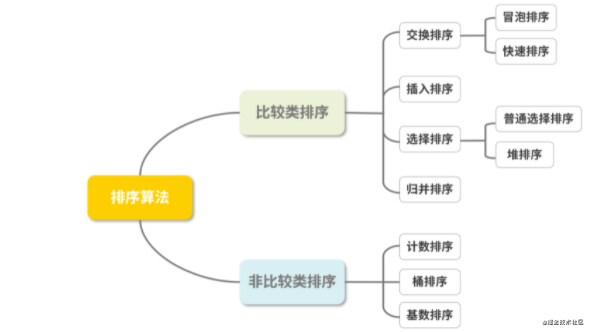
Non comparison sort is rarely used in practice, so this lecture mainly focuses on comparison sort. In fact, according to the stability of sorting, it can also be divided into stable sorting and unstable sorting. For example, quick sorting is unstable sorting, and bubbling sorting is stable sorting. I will help you distinguish again in the final summary.

So let's start with the simplest sort. Let's look at bubble sort first.

Bubble sorting

Bubble sort is the most basic sort, which is generally exposed when you first learn the data structure. Bubble sorting is to compare two elements at a time and exchange them if the order is wrong. The work of visiting the sequence will be repeated until there is no need to exchange, that is, the sequence has been sorted. Look at the code below.

var a = [1, 3, 6, 3, 23, 76, 1, 34, 222, 6, 456, 221];
function bubbleSort(array) {
  const len = array.length
  if (len < 2) return array
  for (let i = 0; i < len; i++) {
    for (let j = 0; j < i; j++) {
      if (array[j] > array[i]) {
        const temp = array[j]
        array[j] = array[i]
        array[i] = temp
      }
    }
  }
  return array
}
bubbleSort(a);  // [1, 1, 3, 3, 6, 6, 23, 34, 76, 221, 222, 456]

As can be seen from the above code, the final return is the ordered result. Because bubble sorting is too basic and simple, I won't repeat it here. Let's take a look at the quick sort method\

If this content is helpful to you, please use your small hand to help add a chicken leg for Xiaobian by clicking this link: http://github.crmeb.net/u/xingfu

Quick sort

The basic idea of quick sort is to divide the records to be arranged into two independent parts through one-time sorting. If the keywords of one part of the records are smaller than those of the other part, the records of these two parts can be sorted separately to achieve the order of the whole sequence.

Look at the code below.

var a = [1, 3, 6, 3, 23, 76, 1, 34, 222, 6, 456, 221];
function quickSort(array) {
  var quick = function(arr) {
    if (arr.length <= 1) return arr
    const len = arr.length
    const index = Math.floor(len >> 1)
    const pivot = arr.splice(index, 1)[0]
    const left = []
    const right = []
    for (let i = 0; i < len; i++) {
      if (arr[i] > pivot) {
        right.push(arr[i])
      } else if (arr[i] <= pivot) {
        left.push(arr[i])
      }
    }
    return quick(left).concat([pivot], quick(right))
  }
  const result = quick(array)
  return result
}

quickSort(a);//  [1, 1, 3, 3, 6, 6, 23, 34, 76, 221, 222, 456]

After the above code is executed on the console, you can also get the expected results. The main idea is to pick out an element from the sequence, which is called "pivot"; Then reorder the sequence, and all elements smaller than the benchmark value are placed in front of the benchmark and those larger than the benchmark value are placed behind the benchmark; After the division is completed, the benchmark is in the middle of the sequence; Then recursively call the quick method to sort the sub sequence (left) less than the reference value element and the sub sequence (right) greater than the reference value element, which is the idea of fast sorting.

Let's take a look at the implementation of insertion sorting.

Insert sort

Insertion sorting algorithm describes a simple and intuitive sorting algorithm. Its working principle is to build an ordered sequence, scan the unordered data from back to front in the sorted sequence, find the corresponding position and insert it, so as to achieve the effect of sorting. Take a look at the code.

var a = [1, 3, 6, 3, 23, 76, 1, 34, 222, 6, 456, 221];
function insertSort(array) {
  const len = array.length
  let current
  let prev
  for (let i = 1; i < len; i++) {
    current = array[i]
    prev = i - 1
    while (prev >= 0 && array[prev] > current) {
      array[prev + 1] = array[prev]
      prev--
    }
    array[prev + 1] = current
  }
  return array
}
insertSort(a); // [1, 1, 3, 3, 6, 6, 23, 34, 76, 221, 222, 456]

From the execution results, it can be found that the sorting effect is realized by inserting sorting. The idea of insertion sorting is to adjust based on the array itself. First, loop traversal starts from i equal to 1, get the current value, and compare it with the previous value. If the previous value is greater than the current value, exchange the previous value with the current value. Through this continuous loop, the purpose of sorting is achieved.

Let's talk about the implementation of selective sorting.

If this content is helpful to you, please use your small hand to help add a chicken leg for Xiaobian by clicking this link: http://github.crmeb.net/u/xingfu

Select sort

Selective sorting is a simple and intuitive sorting algorithm. Its working principle is to first store the smallest element at the beginning of the sequence, then continue to find the smallest element from the remaining unordered elements, and then put it behind the sorted sequence... And so on until all elements are sorted. Look at the code below.

var a = [1, 3, 6, 3, 23, 76, 1, 34, 222, 6, 456, 221];
function selectSort(array) {
  const len = array.length
  let temp
  let minIndex
  for (let i = 0; i < len - 1; i++) {
    minIndex = i
    for (let j = i + 1; j < len; j++) {
      if (array[j] <= array[minIndex]) {
        minIndex = j
      }
    }
    temp = array[i]
    array[i] = array[minIndex]
    array[minIndex] = temp
  }
  return array
}
selectSort(a); // [1, 1, 3, 3, 6, 6, 23, 34, 76, 221, 222, 456]

In this way, the sorting of arrays can also be realized by selecting the sorting method. From the above code, it can be seen that this sorting is one of the most stable sorting algorithms, because no matter what data goes in, it is O(n square) time complexity, so when using it, the smaller the data scale, the better.

Let's see how heap sorting is implemented.

Heap sort

Heap sort is a sort algorithm designed by using the data structure of heap. Heap is a structure that approximates a complete binary tree and satisfies the nature of heap at the same time, that is, the key value or index of a child node is always less than (or greater than) its parent node. The bottom layer of the heap is actually a complete binary tree, which can be realized by array.

The heap with the largest root node is called the large root heap, and the heap with the smallest root node is called the small root heap. You can sort from large to small or from small to large, and establish corresponding heaps respectively. Look at the code below.

var a = [1, 3, 6, 3, 23, 76, 1, 34, 222, 6, 456, 221];
function heap_sort(arr) {
  var len = arr.length
  var k = 0
  function swap(i, j) {
    var temp = arr[i]
    arr[i] = arr[j]
    arr[j] = temp
  }
  function max_heapify(start, end) {
    var dad = start
    var son = dad * 2 + 1
    if (son >= end) return
    if (son + 1 < end && arr[son] < arr[son + 1]) {
      son++
    }
    if (arr[dad] <= arr[son]) {
      swap(dad, son)
      max_heapify(son, end)
    }
  }
  for (var i = Math.floor(len / 2) - 1; i >= 0; i--) {
    max_heapify(i, len)
  }

  for (var j = len - 1; j > k; j--) {
    swap(0, j)
    max_heapify(0, j)
  }

  return arr
}
heap_sort(a); // [1, 1, 3, 3, 6, 6, 23, 34, 76, 221, 222, 456]

From the code point of view, heap sorting is more complex than the above sorting as a whole, which is not easy to understand. However, you should know two points: first, the core point of heap sorting is to build a heap before sorting; Second, the heap is actually a complete binary tree. If the sequence number of the parent node is n, the sequence number of the leaf node is 2n and 2n+1 respectively.

If you understand these two points, it's better to look at the code. At the end of heap sorting, there are two loops: the first is the order of processing parent nodes; The second loop is to adjust the heap according to the size comparison between the parent node and the leaf node. Through the adjustment of these two cycles, the final heap sorting is completed.

Let's look at the last sort of merging.

Merge sort

Merge sort is an effective sort algorithm based on merge operation. This algorithm is a very typical application of divide and conquer method. Merge the ordered subsequences to obtain a completely ordered sequence; First order each subsequence, and then order the subsequence segments. If two ordered tables are merged into one, it is called two-way merging. Let's look at the code first.

var a = [1, 3, 6, 3, 23, 76, 1, 34, 222, 6, 456, 221];

function mergeSort(array) {
  const merge = (right, left) => {
    const result = []
    let il = 0
    let ir = 0
    while (il < left.length && ir < right.length) {
      if (left[il] < right[ir]) {
        result.push(left[il++])
      } else {
        result.push(right[ir++])
      }
    }

    while (il < left.length) {
      result.push(left[il++])
    }

    while (ir < right.length) {
      result.push(right[ir++])
    }

    return result
  }

  const mergeSort = array => {
    if (array.length === 1) { return array }
    const mid = Math.floor(array.length / 2)
    const left = array.slice(0, mid)
    const right = array.slice(mid, array.length)
    return merge(mergeSort(left), mergeSort(right))
  }
  return mergeSort(array)
}

mergeSort(a); // [1, 1, 3, 3, 6, 6, 23, 34, 76, 221, 222, 456]

As you can see from the above code, you can get the desired result by merging and sorting. The idea of divide and conquer is mentioned above. You can see from the mergeSort method that the array can be divided into left and right arrays through mid, recursively call the sorting method for these two arrays, and finally merge the two arrays in order.

Merge sort is a stable sort method. Like selective sort, the performance of merge sort is not affected by the input data, but its performance is much better than selective sort, because it is always O(nlogn) time complexity. The cost is the need for additional memory space.

The above are the six algorithms to realize array sorting to be introduced today. If you are interested, you can learn the three methods of non comparison sorting by yourself.

summary

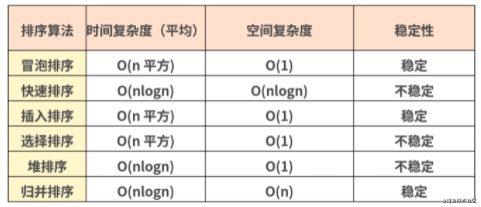
In this lecture, we introduced several sorting methods commonly used in ordinary development. I organized a table and summarized their respective time complexity and space complexity. You can compare them to review the content of this lecture.

If the content of this article is helpful to you, please use your small hand to help make it up for you. Click this link: http://github.crmeb.net/u/xingfu