1. Basic Theory
When processing feature descriptors suitable for multiple images, there are two main feature detection methods, one is angle-based detection, the other is to process all areas in the image. Here we will focus on angle-based detection.
In 1988, Harris and Stephens presented an angle detection algorithm, HS Angle Detector. See paper A Combined Corner and Edge Detector.
The principle of HS detector is as follows: there are three cases of gray level change, one is that gray level does not change in all directions, two is that gray level changes in one direction, and three is that gray level changes in both directions. The HS angle detector uses a mathematical formula to distinguish the three cases.
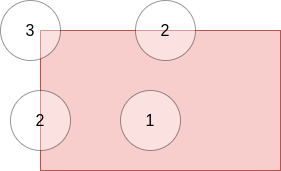
F denotes the image, f(s, t) denotes a small image patch defined by the value of (s, t). f(s+x, t+y) is a small image patch with the same size but moved (x,y). The weighting and representation of the square of the difference between each pixel value of the two image blocks is:
C ( x , y ) = ∑ ∑ ω ( s , t ) [ f ( s + x , t + y ) − f ( s , t ) ] 2 C(x,y) = \sum\sum\omega(s,t)[f(s+x, t+y)-f(s,t)]^2 C(x,y)=∑∑ω(s,t)[f(s+x,t+y)−f(s,t)]2
ω ( s , t ) \omega(s,t) ω (s,t) is a weighted function. Where there is an angle, C(x,y) takes the maximum value. Take a pixel point and calculate it in its neighboring pixels C ( x , y ) C(x,y) C(x,y).
take f ( s + x , t + y ) f(s+x, t+y) f(s+x,t+y) represents the approximation of the Taylor expansion.
f ( s + x , t + y ) ≈ f ( s , t ) + x f x ( s , t ) + y f y ( s , t ) f(s+x, t+y)\approx f(s,t)+xf_x(s,t)+yf_y(s,t) f(s+x,t+y)≈f(s,t)+xfx(s,t)+yfy(s,t)
Then?
C ( x , y ) = ∑ ∑ ω ( s , t ) [ x f x ( s , t ) + y f y ( s , t ) ] 2 C(x,y) = \sum\sum\omega(s,t)[xf_x(s,t)+yf_y(s,t)]^2 C(x,y)=∑∑ω(s,t)[xfx(s,t)+yfy(s,t)]2
The above equations can be expressed as matrices:
C ( x , y ) = [ x , y ] M [ x y ] C(x,y) = [x,y]M\begin{bmatrix} x\\ y \end{bmatrix} C(x,y)=[x,y]M[xy]
Where,
M = ∑ ∑ ω ( s , t ) A M = \sum\sum\omega(s,t)A M=∑∑ω(s,t)A
A = [ f x 2 f x f y f x f y f y 2 ] A = \begin{bmatrix} f_x^2 & f_xf_y\\ f_xf_y & f_y^2 \end{bmatrix} A=[fx2fxfyfxfyfy2]
M M M is sometimes called a Harris matrix.
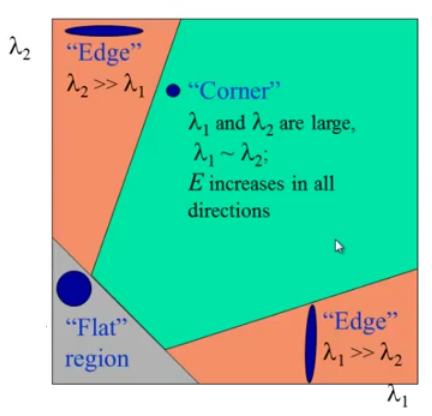
matrix M M The eigenvector of M points to the largest direction of data expansion, and the corresponding eigenvalue is proportional to the amount of data expansion in the direction of the eigenvector. Thus, two small eigenvalues represent an almost constant gray scale, one small eigenvalue and one large eigenvalue represent a vertical or horizontal boundary, and two large eigenvalues represent an isolated point or angle.
However, due to the overhead of calculating the eigenvalues, the HS angle detector does not use the eigenvalues but uses the properties of the square matrix, where the trace equals the sum of the eigenvalues of the matrix and the determinant equals the product of the eigenvalues.
R = λ x λ y − k ( λ x + λ y ) 2 = d e t ( M ) − k t r a c e 2 ( M ) R=\lambda_x\lambda_y - k(\lambda_x + \lambda_y)^2=det(M)-ktrace^2(M) R=λxλy−k(λx+λy)2=det(M)−ktrace2(M)
k k k is a constant, usually ( 0 , 0.25 ) (0, 0.25) (0,0.25).
When both eigenvalues are large, R takes a larger positive value, one larger eigenvalue and one smaller eigenvalue, R takes a larger negative value, and the absolute value of R is smaller when both eigenvalues are small
K can be seen as a sensitivity factor, the smaller k, the more angles are found
Shi-Tomasi corner point detector
In 1994, proposed by Jianbo Shi and Carlo Tomasi Good features to track
Direct use
R
=
m
i
n
(
λ
x
,
λ
y
)
R=min(\lambda_x,\lambda_y)
R=min( λ x, λ y) as a measure, avoiding hyperparameters
k
k
k
2.OpenCV API
2.1cornerHarris
void cv::cornerHarris(
InputArray src,
OutputArray dst,
int blockSize,
int ksize,
double k,
int borderType = BORDER_DEFAULT
)
- src: input, 8-bit single channel image, grayscale
- dst: Stores data from Harris test results, data type CV_32FC1
- blockSize: Neighborhood size when calculating C(x,y)
- ksize: The size of the convolution kernel when calculating gradients using the Sobel operator
- k: The hyperparameter in calculating R, which is the mediator for the sensitivity of angle detection, has more small angles and less large angles.
- borderType: How boundary pixels are handled
2.2 goodFeaturesToTrack
void cv::goodFeaturesToTrack (
InputArray image,
OutputArray corners,
int maxCorners,
double qualityLevel,
double minDistance,
InputArray mask = noArray(),
int blockSize = 3,
bool useHarrisDetector = false,
double k = 0.04
)
The function of this function,
1. Use cornerHarris to calculate the measurement of each angle first
2. Maximum suppression is performed within the neighborhood of 3x3 per pixel
3. The minimum eigenvalue of the Harris matrix corresponding to each angle is less than
q
u
a
l
i
t
y
L
e
v
e
l
∗
m
a
x
(
q
u
a
l
i
t
y
M
e
a
s
u
r
e
M
a
p
(
x
,
y
)
)
qualityLevel*max(qualityMeasureMap(x,y))
Quality Level_max (quality MeasureMap (x, y)), the angle will be discarded
4. Sort the remaining corners in descending order according to quality measure
5. Remove those corners that are less than maxDistance
- Image: single channel image
- corners: the output vector of an angle
- maxCorners: Maximum number of supported detected corners
- Quality Level: Quality level of control angle, e.g. best is 1500, quality level is 0.01, quality measure less than 1500*0.01 will be discarded
- minDistance: Minimum distance between angle and angle
- Mask:mask to control which part of the image is corner detected
- blockSize: Neighborhood size used to calculate the gradient correlation matrix, refer to cornerEigenValsAndVecs
- UseHarris Detector: Is Harris corner detection used
- Hyperparameters for k:Harris corner detection
3. Examples
#include <opencv2/imgproc.hpp>
#include <opencv2/highgui.hpp>
#include <opencv2/imgcodecs.hpp>
#include <iostream>
using namespace cv;
using namespace std;
Mat src, src_gray;
int maxCorners = 23;
int maxTrackbar = 100;
RNG rng(12345);
int thresh = 200;
int max_thresh = 255;
const char* source_window = "Source image";
const char* corners_window = "Corners detected";
void cornerHarris_demo( int, void* );
void goodFeaturesToTrack_Demo( int, void* );
int main( int argc, char** argv )
{
CommandLineParser parser( argc, argv, "{@input | building.jpg | input image}" );
src = imread( samples::findFile( parser.get<String>( "@input" ) ) );
if ( src.empty() )
{
cout << "Could not open or find the image!\n" << endl;
cout << "Usage: " << argv[0] << " <Input image>" << endl;
return -1;
}
cvtColor( src, src_gray, COLOR_BGR2GRAY );
namedWindow( source_window );
createTrackbar( "Threshold: ", source_window, &thresh, max_thresh, cornerHarris_demo );
imshow( source_window, src );
// cornerHarris_demo( 0, 0 );
goodFeaturesToTrack_Demo( 0, 0 );
waitKey();
return 0;
}
void cornerHarris_demo( int, void* )
{
int blockSize = 2;
int apertureSize = 3;
double k = 0.04;
Mat dst = Mat::zeros( src.size(), CV_32FC1 );
cornerHarris( src_gray, dst, blockSize, apertureSize, k );
Mat dst_norm, dst_norm_scaled;
normalize( dst, dst_norm, 0, 255, NORM_MINMAX, CV_32FC1, Mat() );
convertScaleAbs( dst_norm, dst_norm_scaled );
for( int i = 0; i < dst_norm.rows ; i++ )
{
for( int j = 0; j < dst_norm.cols; j++ )
{
if( (int) dst_norm.at<float>(i,j) > thresh )
{
circle( dst_norm_scaled, Point(j,i), 5, Scalar(0), 2, 8, 0 );
}
}
}
namedWindow( corners_window );
imshow( corners_window, dst_norm_scaled );
imwrite("corner_grid.png", dst_norm_scaled);
}
void goodFeaturesToTrack_Demo( int, void* )
{
maxCorners = MAX(maxCorners, 1);
vector<Point2f> corners;
double qualityLevel = 0.01;
double minDistance = 10;
int blockSize = 3, gradientSize = 3;
bool useHarrisDetector = false;
double k = 0.04;
Mat copy = src.clone();
goodFeaturesToTrack( src_gray,
corners,
maxCorners,
qualityLevel,
minDistance,
Mat(),
blockSize,
gradientSize,
useHarrisDetector,
k );
cout << "** Number of corners detected: " << corners.size() << endl;
int radius = 8;
for( size_t i = 0; i < corners.size(); i++ )
{
circle( copy, corners[i], radius, Scalar(0, 0, rng.uniform(0, 256)), FILLED );
}
namedWindow( source_window );
imwrite("corner_grid_st.png", copy);
imshow( source_window, copy );
}
