Huffman coding
Huffman coding is mainly used in information compression. It is a coding method with high compression efficiency at present. When implementing Huffman coding, binary tree is used for implementation.
Here is a simple example of Huffman coding. For an article, extract all the words and the number of occurrences. Then how to encode these words according to the number of occurrences of these words, so as to make the final article composed of coding as short as possible.
Optimal binary tree
Before introducing how to realize Huffman coding, first learn and understand the optimal binary tree in the binary tree. Let's first define some of these nouns:
- Path: the branch from one node to another in the tree constitutes the path between the two nodes.
- Path length: the number of branches on the path.
- Tree path length: the sum of the path lengths from the tree root to each node.
- Weighted path length of a node: the product of the path length from the node to the tree root and the weight on the node.
- Weighted path length of tree( W P L WPL WPL): the sum of the weighted path lengths of all leaf nodes in the tree.
After that, the weighted path length of the tree is mainly used(
W
P
L
WPL
WPL), here is a simple example.
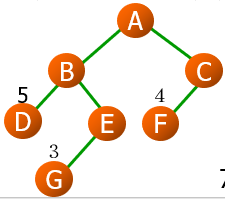
In the above example W P L = 5 ∗ 2 + 3 ∗ 3 + 4 ∗ 2 = 27 WPL=5*2+3*3+4*2=27 WPL=5∗2+3∗3+4∗2=27.
Next, the definition of optimal binary tree is given, assuming that the binary tree is composed of n n n leaves, each leaf node with weight w i w_i wi, then the weighted path length W P L WPL The smallest binary tree of WPL is called optimal binary tree or Huffman tree.
As defined above, and W P L WPL The definition of WPL shows that for the optimal binary tree, the lower the weight value of the leaf node, the greater its depth, that is, it should be at the bottom, while the higher the weight value of the leaf node, the smaller its depth. Only in this way can it be guaranteed W P L WPL WPL should be as small as possible.
Huffman tree structure
When constructing Huffman tree, first of all, our original data only has the symbol represented by each leaf node and the corresponding weight value. At the same time, we also know that we should put the lower weight in the deeper position and the higher weight in the shallower position.
Referring to the previous establishment process of binary tree, it is generally established from top to bottom. However, Huffman tree is just the opposite. It is built from bottom to top, because to meet the needs of location mentioned earlier, the establishment process of Huffman tree is as follows.
- According to the given n n n weights ( w 1 , w 2 , . . . , w n ) (w_1,w_2,...,w_n) (w1, w2,..., wn) composition n n Set of n binary trees F = { T 1 , T 2 , . . . , T n } F=\left\{T_1,T_2,...,T_n \right\} F={T1, T2,..., Tn}, where each binary tree T i T_i Only one of Ti with weight is w i w_i The root node of wi , and the left and right subtrees are empty.
- stay F F In F, select the tree with the smallest weight of the two root nodes as the left and right subtrees to construct a new binary tree, and set the weight of its root node as the sum of the weight of the root nodes of its left and right subtrees
- stay F F Delete the two trees in F and add the new binary tree F F In F.
- Repeat 2 and 3 until F F F contains only one tree.
According to the above process, multiple binary trees can be combined into a binary tree. Here, the above algorithm is simply executed through several examples.
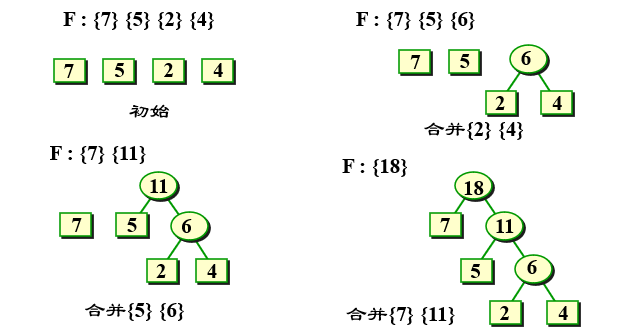
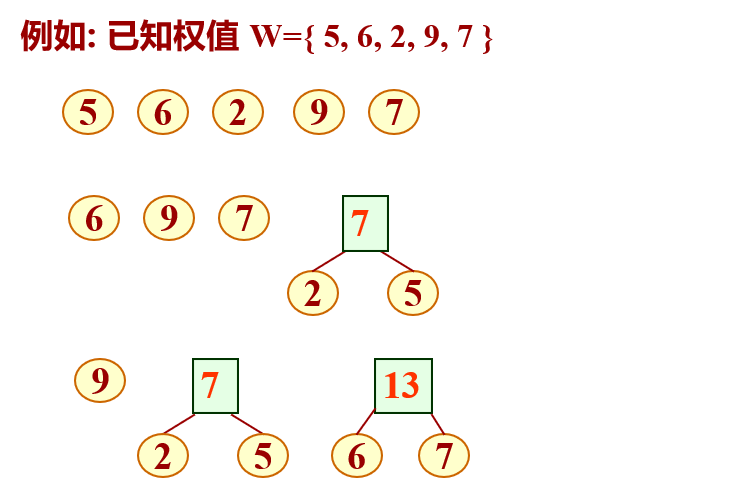
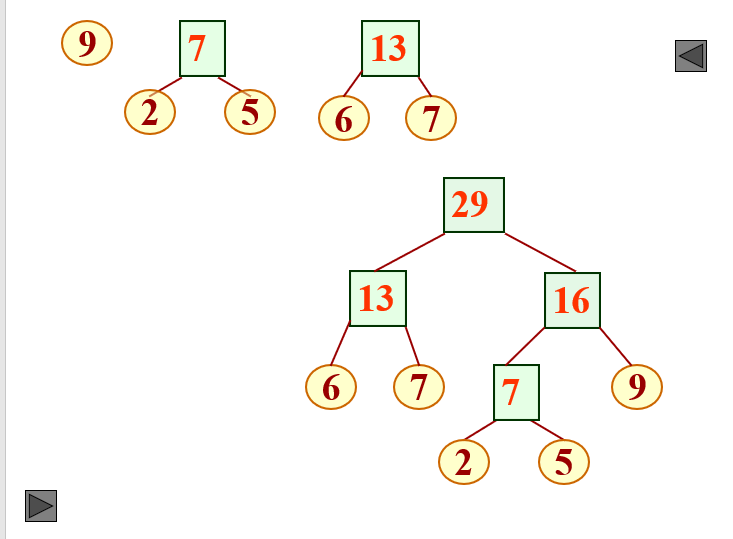
As for the code implementation part, the static linked list is used to implement it, but it is generally divided into two structures, the first is the node in the tree, and the second is the whole Huffman tree.
For each node, since the post order encoding process is from bottom to top and the decoding process is from top to bottom, for each node, it is necessary to know who its left and right children and parents are, as well as the encoding, original data, weight and other information. Therefore, the node class is defined as follows.
#include <iostream>
#include <string>
using namespace std;
// node
typedef struct HuffmanNode
{
char data; // Coded symbol
int weight; // Weight, frequency
int left; // Left child
int right; // Right child
int parent; // parents
string code; // Coded symbol
// Constructor
HuffmanNode()
{
// cout << "node" << endl;
weight = -1;
left = -1;
right = -1;
parent = -1;
data = '#';
code = "";
}
}HuffmanNode;
In the implementation of Huffman tree, static linked list is used, that is, array is used to save each node. Suppose at the beginning n n n leaf nodes, then according to the previous algorithm, two nodes are combined into one, and a total of two leaf nodes will be generated n − 1 n-1 n − 1 new node, so there will be 2 n − 1 2n-1 2n − 1 node. So array development 2 n − 1 2n-1 2n − 1 space is enough. During initialization, the front n n n spaces are used to store leaf nodes, and the subsequent spaces are stored in order according to the generated nodes.
// tree
typedef struct HuffmanTree
{
string info; // Original information
HuffmanNode* tree; // Huffman tree
int num; // Number of leaf nodes
// Constructor
HuffmanTree()
{
info = "";
tree = NULL;
num = 0;
}
}
In the previous algorithm, we need to find the two root nodes with the lowest weight each time, and then merge the two binary trees. Here, the small one is on the left and the large one is on the right. In the search process, use directly C + + C++ References in C + + and simple violent traversal of existing nodes. However, it should be noted that you need to find nodes that have not been added, that is, nodes without parents.
// Find the node with the smallest weight and the second smallest weight
void Select2Min(int pos, int& min1, int& min2)
{
int w1 = 1000000;
// Find the node with the lowest weight
for (int i = 0; i < pos; i++)
{
// cout << tree[i].parent << " " << tree[i].weight << endl;
// No parents and less weight
if (tree[i].parent == -1 && w1 > tree[i].weight)
{
w1 = tree[i].weight;
min1 = i;
}
}
int w2 = 1000000;
// Find the node with the second smallest weight
for (int i = 0; i < pos; i++)
{
if (i == min1) // Avoid the same as before
continue;
if (tree[i].parent == -1 && w2 > tree[i].weight)
{
w2 = tree[i].weight;
min2 = i;
}
}
}
After finding the subscript of the two nodes with the lowest weight, next you need to generate a new node, set the parents of the two nodes as the subscript of the new node according to the operation, set the relationship between the left child and the right child of the new node, and update the weight value of the new node.
// Establish Huffman tree
void createTree(char element[], int weights[], int n)
{
if (n < 2) // Prevent array out of bounds
return;
// initialization
num = n; // Quantity to be coded
tree = new HuffmanNode[2 * n - 1]; // Open up space
if (tree == NULL) // Successful application
return;
for (int i = 0; i < n; i++) // Initialize leaf node first
{
tree[i].data = element[i];
tree[i].weight = weights[i];
// cout << tree[i].data << " " << tree[i].weight << endl;
}
for (int i = n; i < 2 * n - 1; i++)
{
int min1 = -1; // Minimum node
int min2 = -1; // The second small node
Select2Min(i, min1, min2); // Select the smallest and second smallest nodes
// cout << min1 << " " << min2 << endl;
tree[i].weight = tree[min1].weight + tree[min2].weight; // Weight calculation
// Relationship confirmation
tree[min1].parent = i;
tree[min2].parent = i;
tree[i].left = min1;
tree[i].right = min2;
}
}
Huffman tree coding
After the construction and establishment of Huffman tree, the coding process is not completed. In general, what we want is to encode the leaf nodes. In the Huffman tree, we construct a total tree and save all the nodes to be encoded in the total tree in the form of leaf nodes. Then, when coding, start from the root node and traverse the left child once, the coding will be added " 0 " "0" "0". If the child traverses to the right once, the code will be added " 1 " "1" "1".
For convenience, the coding is usually traversed from the leaf node from bottom to top, and each leaf node can go up. However, the code obtained in this way is reversed. Finally, you need to transpose the obtained code once.
// Calculate leaf code
void getCode()
{
if (tree == NULL) // Pointer is not null
return;
// Coding node by node
for (int i = 0; i < num; i++)
{
int now = i; // Child node
int par = tree[i].parent; // Parent node
while (par != -1) // All the way up to the root node
{
if (now == tree[par].left) // If the child node is the left child of the parent node, add 0
tree[i].code += "0";
if (now == tree[par].right) // If the child node is the right child of the parent node, add 1
tree[i].code += "1";
now = par; // Update node and parent node
par = tree[par].parent;
}
reverse(tree[i].code.begin(), tree[i].code.end()); // String inversion
// cout << tree[i].data << " " << tree[i].code << endl;
}
}
After obtaining the code, the next step is the example, that is, coding according to a string of information entered by the user. This implementation is very simple. Search directly according to the words in the information. After finding the corresponding leaf node, add its code.
// code
string encode(string s)
{
if (tree == NULL) // Pointer is not null
return "NULL";
string ans = ""; // Coding results
// Character by character encoding
for (int i = 0; i < (int)s.size(); i++)
{
// Match according to each character, find the corresponding code and add it
for (int j = 0; j < num; j++)
{
if (tree[j].data == s[i]) // Judge whether the leaf node character matches the current character
ans += tree[j].code;
}
}
return ans;
}
Huffman tree decoding
For the decoding process, that is to analyze the original meaning according to a string of codes input by the user. First, ignore the error. Assuming that the encoding is correct, the decoding starts from the root node. If an error occurs 0 0 0 traverses the left child of the current node. If encountered 1 1 1 traverses the right child of the current node. If a leaf node is encountered during traversal, it means that a symbol has been successfully parsed, and then return to the root node to continue the previous encoding and decoding.
Next, consider the error. First, after turning left or right, there is no node, that is, a non-existent node is accessed. At this time, it indicates that there is an error in the intermediate code. After that, there is redundant data or less data at the end. In this case, the intermediate coding is normal. However, after all codes are parsed, it is found that the current pointer does not point to the root node, which indicates that the last part of the codes are not parsed successfully.
// decode
string decode(string s)
{
if (tree == NULL) // Pointer is not null
return "NULL";
string ans = ""; // Decoding result
int index = 2 * num - 2; // Decoding from the root node down
// Decode character by character
for (int i = 0; i < (int)s.size(); i++)
{
if (s[i] == '0') // Turn left at 0
index = tree[index].left;
if (s[i] == '1') // Turn right at 1
index = tree[index].right;
if (index == -1) // If a nonexistent node is accessed, it indicates decoding error
return "error";
// If a leaf node is encountered, a character is decoded successfully, and then traversal starts from the root node again
if (tree[index].left == -1 && tree[index].right == -1)
{
ans += tree[index].data;
index = 2 * num - 2;
}
}
if (index != 2 * num - 2) // Redundant encoding at the end is also a decoding error
return "error";
return ans;